风速Weibull分布和光伏Beta分布的参数拟合方法(含matlab算例)

本文主要是介绍风速Weibull分布和光伏Beta分布的参数拟合方法(含matlab算例)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在风光场景生成、随机优化调度等研究中，常常假设风速服从Weibull分布，太阳辐照度服从Beta分布。那我们如何得到两个分布的参数呢？文本首先介绍了风速Weibull分布和辐照度Beta分布的基本概率模型及其性性质，之后以MATLAB代码为例阐述了如何根据历史观测数据对两种分布的参数进行估计。

Weibull分布

风机出力的不确定性主要来源于风速固有的间歇性、随机性和波动性，学术界及工业均普遍认为风速的概率分布服从经典的两参数“Weibull分布”。风速的Weibull分布的概率密度函数(Probability Density Function, PDF)为：

 

Weibull 分布的均值与方差：

• Weibull分布的均值为：

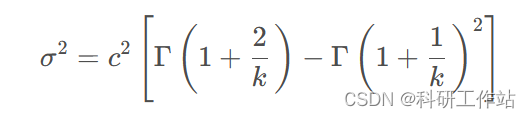
参数估计

两种方法

• 利用MATLAB自带的 fitdist 函数直接对历史观测数据进行拟合

% 分别对NT个时刻的风速数据进行Weibull分布拟合
% 首先要准备一个风速数据windspeed，维度为(N, NTime)
% 其中，N为样本个数，NTime为时刻数如24for i = 1 : NTimewif = fitdist(windspeed(:, i), 'weibull');k_wif(i) = wif.B;c_wif(i) = wif.A;
end

• 利用随机变量的期望和方差计算参数：包括SDM和MOM两种

% 计算风速均值
wind_speed_avg = mean(windspeed);
% 计算风速标准差
wind_speed_std = std(windspeed);% 标准差法参数计算 standard deviation method 
k_wstdm = (wind_speed_std./wind_speed_avg).^-1.086;
c_wstdm = (wind_speed_avg)./(gamma(1+(1./k_wstdm)));% 矩量法参数计算 Method of Moments Method Factor Calculation
k_mom = (0.9874./(wind_speed_std./wind_speed_avg)).^1.0983;
c_mom = (wind_speed_avg)./(gamma(1+(1./k_mom)));

Beta分布

Beta 分布的均值与方差：

• Beta 分布的期望

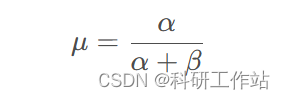
 Beta 分布的方差

参数估计

两种方法

• 利用MATLAB自带的 fitdist 函数直接对历史观测数据进行拟合

% NTime为时刻数，如24
% NS 为观测数据维度
% solardat为历史观测数据，维度为(NS, NTime)solardata = solardata / max(max(solardata)); % 因为Beta分布是定义在(0,1) 区间的连续概率分布
for i = 1 : NTimeparas = fitdist(solardata(:, i), 'beta');a(i) = paras.a;b(i) = paras.b; 
end% 会报错“如果所有数据值都相同，则不能拟合beta分布”，因为夜间出力为0，所以可以不对0拟合

 

• 利用历史观测数据的期望和方差求出Beta的两个参数

% NTime为时刻数，如24
% NS 为观测数据维度
% solardat为历史观测数据，维度为(NS, NTime)solardata = solardata / max(max(solardata))% 计算均值
si_avg = mean(solardata);
% 计算标准差
si_std = std(solardata).^2;a = zeros(1, NTime);
b = zeros(1, NTime);
for i = 1 : NTimea(i) = si_avg(i) * ( si_avg(i) * (1 - si_avg(i))/si_std(i) - 1 );b(i)  = (1 - si_avg(i)) * ( si_avg(i) * (1 - si_avg(i))/si_std(i) - 1);
enda(isnan(a))=0;
b(isnan(b))=0;

这篇关于风速Weibull分布和光伏Beta分布的参数拟合方法(含matlab算例)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---