24.4.14周报

本文主要是介绍24.4.14周报，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

星期一：

牛客小白月赛90 补F 牛客传送门

官方题解

思路：dp【d】【i】【j】表示考虑到第d条线段，0-i 至少被覆盖了两次，i-j 恰好被覆盖一次，j-n 未被覆盖的方案数

先对数据进行离散化处理，将枚举线段和左右端点的复杂度变为O(m^3)

对线段进行左右端点升序排序，可确保未转移的即非法状态，此外st【i】细节减一，是为了转移状态时更好判断和被枚举区间左端点的大小关系（枚举区间点全为离散化端点

代码如下：

const int mod=998244353;
ll n;
int m;
int st[220],ed[220];
PII a[220];
vector<int>ve;
ll dp[404][404][404];
void solve(){cin >> n >> m;for(int i=1;i<=m;i++){cin >> st[i] >> ed[i]; st[i]--;ve.push_back(st[i]);ve.push_back(ed[i]);}ve.push_back(0),ve.push_back(n);sort(ve.begin(),ve.end());ve.erase(unique(ve.begin(),ve.end()),ve.end());for(int i=1;i<=m;i++){st[i]=lower_bound(ve.begin(),ve.end(),st[i])-ve.begin();ed[i]=lower_bound(ve.begin(),ve.end(),ed[i])-ve.begin();a[i]={st[i],ed[i]};}sort(a+1,a+m+1);dp[0][0][0]=1;int sz=ve.size();for(int d=1;d<=m;d++){for(int i=0;i<sz;i++){for(int j=i;j<sz;j++){if(!dp[d-1][i][j]) continue;dp[d][i][j]+=dp[d-1][i][j],dp[d][i][j]%=mod;if(a[d].first>i) continue;dp[d][max(1ll*i,min(1ll*j,a[d].second))][max(1ll*j,a[d].second)]+=dp[d-1][i][j];dp[d][max(1ll*i,min(1ll*j,a[d].second))][max(1ll*j,a[d].second)]%=mod;}}}cout << dp[m][sz-1][sz-1];
}

ATC abc348 D atc传送门

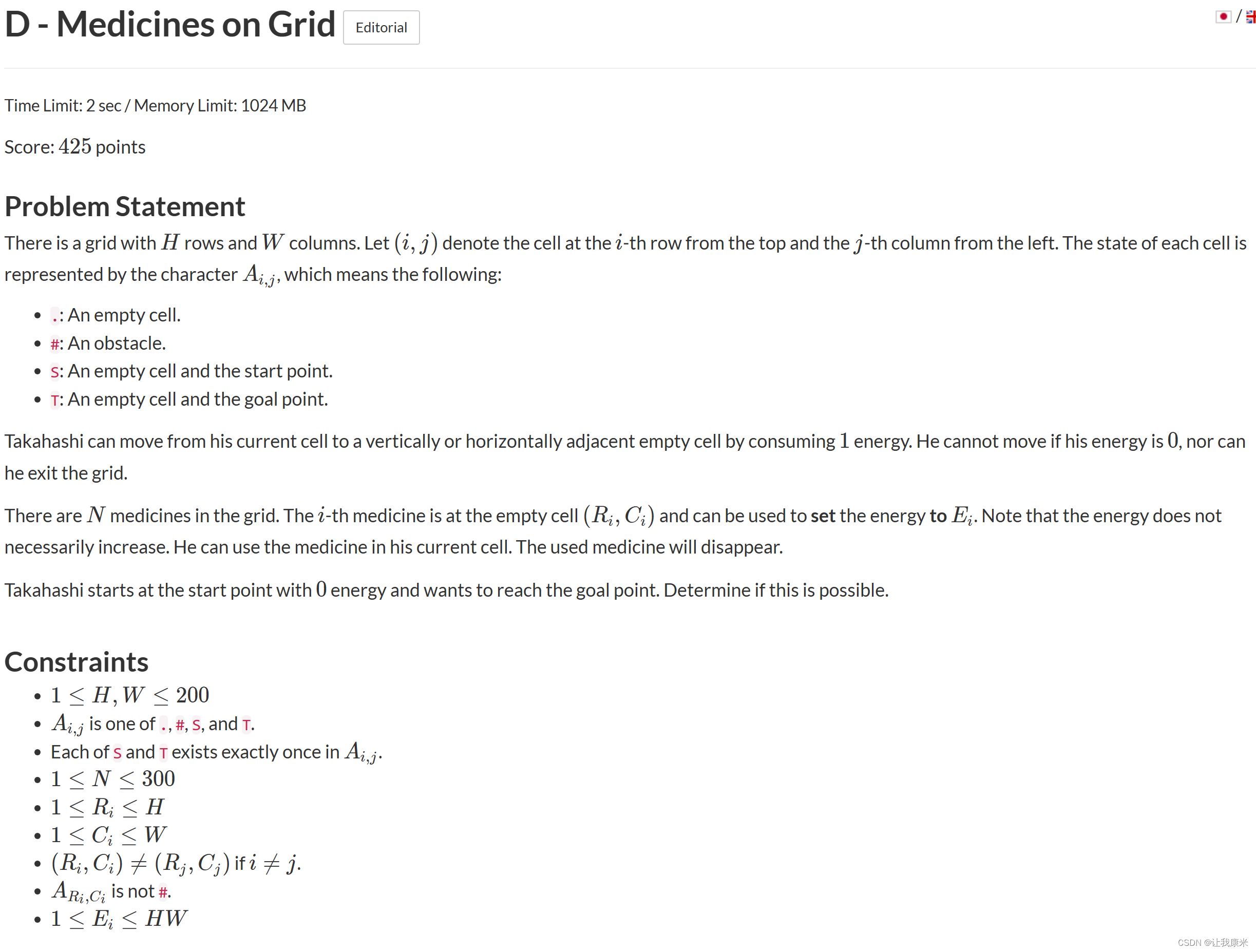
思路：赛时看到没一点思路，后来用bfs想，想一会就大概能写了

从起点开始搜，不用vi数组，转而用到达每格的能量值剪枝，到过终点就标记

是否嗑药可以选择，放在出发时判断更方便写

代码如下：

ll n;
char a[220][220];
int h,w,sx,sy,fx,fy;
map<PII,int>mp;
bool if1[220][220];
int e[220][220];
int dx[]={0,0,-1,1};
int dy[]={1,-1,0,0};
void solve(){cin >> h >> w;for(int i=1;i<=h;i++){for(int j=1;j<=w;j++){cin >> a[i][j];if(a[i][j]=='S') sx=i,sy=j;if(a[i][j]=='T') fx=i,fy=j;}}cin >> n;for(int i=1;i<=n;i++){int r,c,e; cin >> r >> c >> e;if1[r][c]=1;mp[{r,c}]=e;}queue<PII>qu;if(!if1[sx][sy]){cout << "No"; return ;}e[sx][sy]=mp[{sx,sy}];qu.push({sx,sy});bool if3=0;while(qu.size()){auto [x,y]=qu.front(); qu.pop();if(if1[x][y]) e[x][y]=max(mp[{x,y}],e[x][y]);      //是否嗑药if(e[x][y]==0) continue;for(int i=0;i<4;i++){int xx=x+dx[i],yy=y+dy[i];if(a[xx][yy]=='#' || xx<1 || xx>h || yy<1 || yy>w) continue;if(xx==fx && yy==fy) if3=1;if(e[x][y]>1 && e[xx][yy]>=e[x][y]-1) continue;     //剪枝e[xx][yy]=e[x][y]-1;qu.push({xx,yy});}}if(if3) cout << "Yes\n";else cout << "No\n";
}

星期二：

昨晚round938 div3把global上的分又掉回来了

补D：

思路：一开始用multiset存b数组，然后用find和erase函数匹配a，容器size <= m-k即符合条件，

i > m时若 a【i-m】被匹配过就insert回去，但wa，测了半天发现了 4 2 2 3 1 1 3 1 3这个样例，但最后10min没改出来

以上思路的问题是，例如3 1 1 3，第二个1匹配了，导致第三个1没有匹配到，当还回第二个1时，第三个1依然不会被匹配

于是改为用map当桶存，对每个i 都进行mp【a【i】】- -，即使减后小于0也要减1，这样不会漏掉匹配的字符

代码如下：

const int N=2e6+10,M=210;
const int mod=998244353;
ll n;
ll m,k;
int a[N];
void solve(){cin >> n >> m >> k;for(int i=1;i<=n;i++) cin >> a[i];map<int,int>mp;for(int i=1;i<=m;i++){int x; cin >> x;mp[x]++;}ll ans=0,cnt=0;for(int i=1;i<=m;i++) cnt+=mp[a[i]]-->0;ans+=cnt>=k;for(int i=m+1;i<=n;i++){cnt-=++mp[a[i-m]]>0;cnt+=mp[a[i]]-->0;ans+=cnt>=k;}cout << ans << "\n";
}

下午蓝桥杯

补I：洛谷传送门

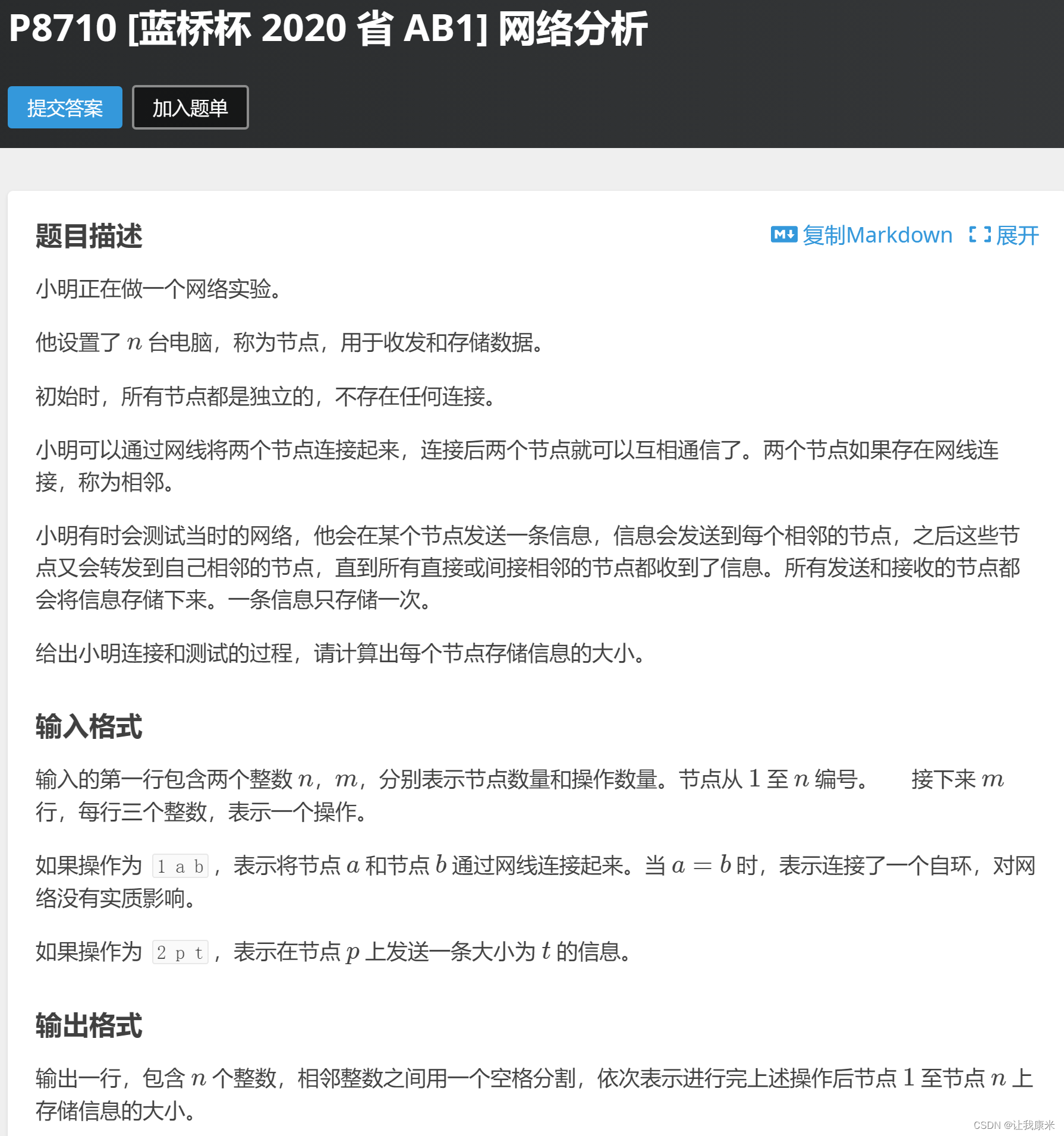
暴力写唐了，又把 fnd ( i )写成fa【i】了，woyouzui

思路：并查集，但暴力复杂度为 O(n*m)，考虑如何优化

这里先说一个很离奇的优化方式，能过，即在 find函数前加 inline

inline，一个很神奇的东西，简单来说就是让函数内置，避免频繁的函数调用，适用于并查集的find函数这种代码结构简单，调用次数多的，真的很神奇，当然也有蓝桥杯数据弱的原因

inline int fnd(int x){return fa[x]==x?x:fa[x]=fnd(fa[x]);
}

正解有点看不懂，先放着

补F：洛谷传送门

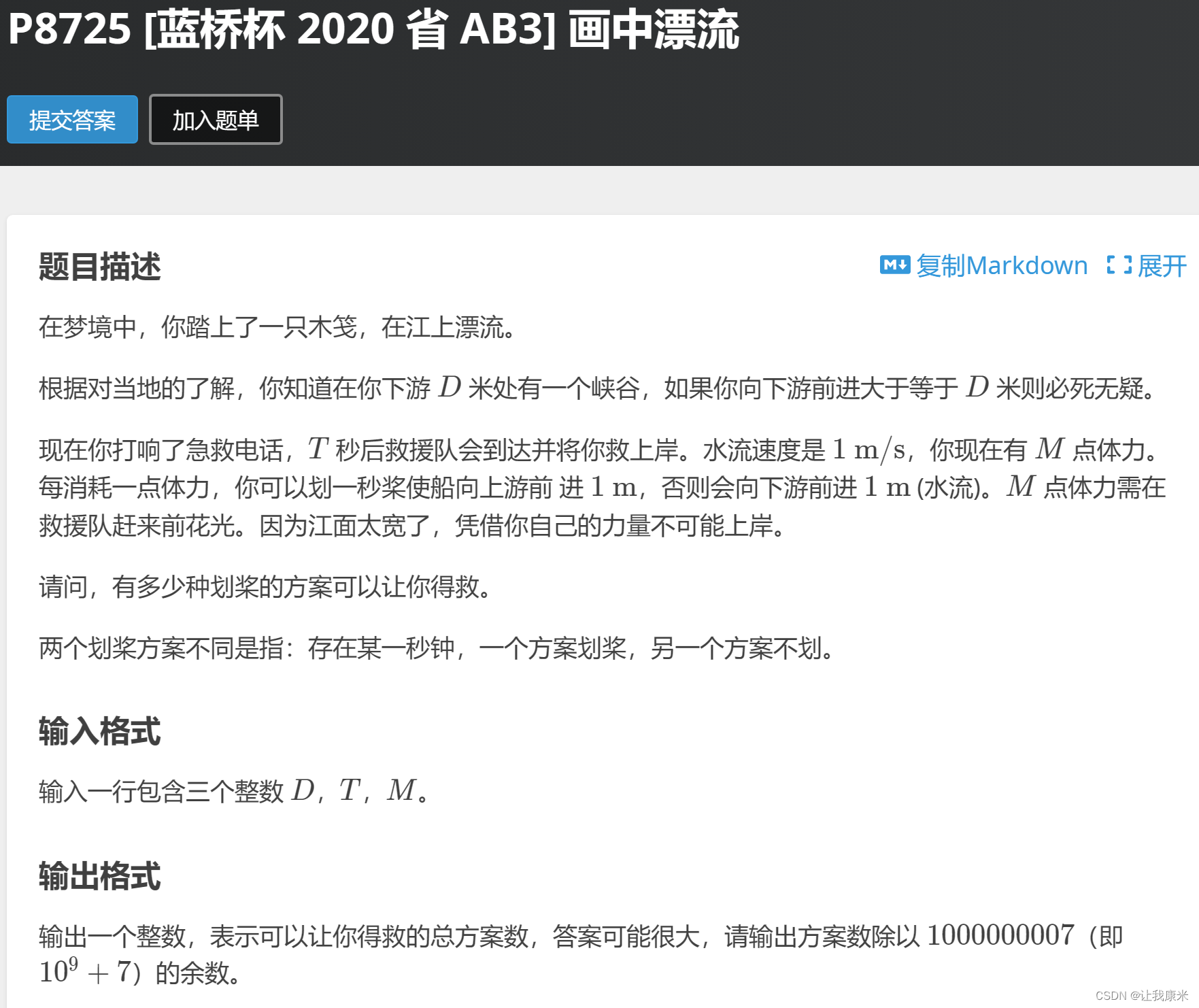
思路：试过几个状态，只有一个状态能转移出来，dp【i】【j】表示第 i 时刻还剩 j 体力

如果此状态还没有掉下峡谷，即可转移，dp【i】【j】= dp【i-1】【j】+ dp【i-1】【j+1】

代码如下：

const int mod=1e9+7;
ll n;
ll d,t,m;
ll dp[3030][1510];
void solve(){cin >> d >> t >> m;dp[0][m]=1;for(int i=1;i<=t;i++){for(int j=m;j>=0;j--){if(i-2*(m-j)>=d) continue;dp[i][j]+=dp[i-1][j]+dp[i-1][j+1];dp[i][j]%=mod;}}cout << dp[t][0];
}

补G：

思路：建立分层图，因为要选边，最多选两条，所以建三层图，若一条路无限高杆，则在三层图里各自建立双向边，否则建立一层到下一层的单向边，u到下一层的v和v到下一层的u，后者别漏了

这样通过一条边跑到下一层就相当于拆除了一根限高杆，跑个常规 dij 即可

代码如下：

const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
int m;
struct nod{int nex,to,w;
}e[N];
int hd[N],cnt;
void add(int u,int v,int w){e[++cnt].to=v;e[cnt].w=w;e[cnt].nex=hd[u];hd[u]=cnt;
}
ll dis[N];
bool vi[N];
void dij(){memset(dis,0x3f,sizeof dis);priority_queue<PII,vector<PII>,greater<PII>>pq;pq.push({0,1});dis[1]=0;while(!pq.empty()){auto [d,t]=pq.top(); pq.pop();if(vi[t]) continue;vi[t]=1;for(int i=hd[t];i;i=e[i].nex){int v=e[i].to,w=e[i].w;if(dis[v]<=d+w) continue;dis[v]=d+w;pq.push({dis[v],v});}}
}
void solve(){cin >> n >> m;while(m--){int a,b,c,d; cin >> a >> b >> c >> d;if(!d){                                     //没限高杆add(a,b,c),add(b,a,c);add(a+n,b+n,c),add(b+n,a+n,c);add(a+2*n,b+2*n,c),add(b+2*n,a+2*n,c);  //在三层图都建双向边}else{add(a,b+n,c),add(b,a+n,c);add(a+n,b+2*n,c),add(b+n,a+2*n,c);      //u到下一层的v,和v到下一层的u  }}dij();ll res=min({dis[n],dis[2*n],dis[3*n]});cout << dis[n]-res;
}

星期三：

上午vp了场cf round914 div2，做了一题就卡B，然后睡觉去了

B操作比较繁琐，de了半天（真正意义上的半天）才ac，也是我太粗糙了

B： cf传送门

思路：先对数组排序，再前缀和处理

对于a【i】，它前面的数肯定是可以拿下的，所以直接取前缀和sum【i】，然后往后遍历，当遍历到a【r】大于等于sum【r-1】时结束，那么对a【i】来说，他的答案就是r-2（r-1个数减去自己）

如果这么做的话，复杂度依然是O(n^2)，但还有一个关键点，a【i】遍历到了a【r】前，那么其实从a【i】到a【r-1】，答案都是一样的，即r-2，那么下一次 i 就可以跳到 r，复杂度即O(n)

代码如下：

const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
PII a[N];
ll sum[N];
int ans[N];
void solve(){cin >> n;for(int i=1;i<=n;i++){cin >> a[i].first;a[i].second=i;}sort(a+1,a+n+1);for(int i=1;i<=n;i++) sum[i]=sum[i-1]+a[i].first;for(int i=1;i<=n;i++){ll t=sum[i];int r;for(r=i+1;r<=n;r++){if(a[r].first>t) break;t+=a[r].first;}for(int k=i;k<r;k++) ans[a[k].second]=r-2;i=r-1;                                      //因为有i++，所以注意要减一}for(int i=1;i<=n;i++) cout << ans[i] << " \n"[i==n];
}

下午集美校赛，被两道不该卡的题卡了会，没做到的题再继续补

cf 914 C cf传送门

思路:初见时确实没思路,直接看的题解

k>=3时, 因可以重复选一样的 i , j 两次, 第三次必有两个相同的值, 故答案为0

k==1时, 遍历n找出最小的a[i+1] - a[i], 和a[1]取min, 即为答案

k==2时, 进行n^2的遍历, 每次遍历二分找出a[j] - a[i] 最接近的值, 不断取min,复杂度O(n^2 logn)

数据范围很大,记得都开ll

代码如下:

const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
int k;
ll a[N];
void solve(){cin >> n >> k;for(int i=1;i<=n;i++) cin >> a[i];if(k>=3){cout << "0\n"; return ;}sort(a+1,a+n+1);ll mi=a[1];for(int i=1;i<n;i++) mi=min(a[i+1]-a[i],mi);if(k==1){cout << mi << "\n"; return ;}for(int i=1;i<=n;i++){for(int j=i+1;j<=n;j++){ll val=a[j]-a[i];int idx=lower_bound(a+1,a+n+1,val)-a;if(idx<=n) mi=min(a[idx]-val,mi);if(idx>1) mi=min(val-a[idx-1],mi);}}cout << mi << "\n";
}

星期四：

集美校赛往后做了一题，较简单，后面的题看着比较繁琐，暂时弃掉

星期二蓝桥杯训练赛的F：

思路：星期二用dp 补了一次，这次用记忆化搜索再写一遍

这次二补的时候想到，如果我当时写dp时，用记忆化搜索的思路思考下，会很自然想到时间和剩余体力是俩重要的参数，可能就能把dp状态找出来了

代码如下：

const int mod=1e9+7;
ll n;
ll d,t,m;
ll dp[3030][1510];
int dfs(int ti,int lef){if(ti==t){if(lef>0) return 0;return 1;}if(dp[ti][lef]!=-1) return dp[ti][lef];    //记忆化处理if(ti-2*(m-lef)>=d) return dp[ti][lef]=0;  //掉下峡谷ll res=0;if(lef==0) res+=dfs(ti+1,0),res%=mod;    //体力为0，只能不划else{res+=dfs(ti+1,lef-1),res%=mod;       //体力有剩，两种选择res+=dfs(ti+1,lef),res%=mod;}return dp[ti][lef]=res;
}
void solve(){cin >> d >> t >> m;memset(dp,-1,sizeof dp);                 //记忆化搜索的初始化ll ans=dfs(0,m);cout << ans;
}

牢王拉的dp题单，和区域赛签到题题单，举步维艰

星期五，六：

打了蓝桥杯，发挥的不咋样

cf掉下青了

周日：

队内打了场全是模拟的天梯赛，麻了

补了下昨晚cf round929 div2 的C，构造 cf传送门

思路：首先答案一定可以是以下这种形式（相信permutation

其一构造方法为，先填第一行的n到1，然后 i 从2到 n，先填 i 列，再填 i 行的n到1

代码如下：

ll n;
void solve(){cin >> n;ll sum=0;for(int i=1;i<=n;i++) sum+=i*(2*i-1);       //sum可直接计算cout << sum << " " << 2*n-1 << "\n";        //修改次数也固定为2n-1cout << "1 1 ";for(int i=n;i;i--) cout << i << " \n"[i==1];for(int i=2;i<=n;i++){cout << "2 " << i << " ";for(int j=n;j;j--) cout << j << " \n"[j==1];cout << "1 " << i << " ";for(int j=n;j;j--) cout << j << " \n"[j==1];}
}

击败大树守卫，战斗，爽