本文主要是介绍力扣2923、2924.找到冠军I、II---(简单题、中等题、Java、拓扑排序),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、找到冠军I
思路描述:
代码:
二、找到冠军II
思路描述:
代码:
一、找到冠军I
一场比赛中共有 n 支队伍,按从 0 到 n - 1 编号。
给你一个下标从 0 开始、大小为 n * n 的二维布尔矩阵 grid 。对于满足 0 <= i, j <= n - 1 且 i != j 的所有 i, j :如果 grid[i][j] == 1,那么 i 队比 j 队 强 ;否则,j 队比 i 队 强 。
在这场比赛中,如果不存在某支强于 a 队的队伍,则认为 a 队将会是 冠军 。
返回这场比赛中将会成为冠军的队伍。
示例 1:
输入:grid = [[0,1],[0,0]] 输出:0 解释:比赛中有两支队伍。 grid[0][1] == 1 表示 0 队比 1 队强。所以 0 队是冠军。
示例 2:
输入:grid = [[0,0,1],[1,0,1],[0,0,0]] 输出:1 解释:比赛中有三支队伍。 grid[1][0] == 1 表示 1 队比 0 队强。 grid[1][2] == 1 表示 1 队比 2 队强。 所以 1 队是冠军。
思路描述:
这个题属于简单题,我们只要给出一个起始队伍的编号即可,从该队伍编号开始,遍历二维数组,如果有大于本身的,即强于本身的,就将编号改编为强于本身的那个编号,然后,再从该编号开始进行遍历,最多遍历n次才才找到,因此时间复杂度为O(n*m)。
代码:
class Solution {public int findChampion(int[][] grid) {int maxIndex=0;int n=grid.length;int m=grid[0].length;for(int j=0;j<m;j++){int falg=0;for(int i=0;i<n;i++){if(grid[i][maxIndex]==1){maxIndex=i;falg=1;break;}}if(falg==0){return maxIndex;}}return maxIndex;}
}二、找到冠军II
一场比赛中共有 n 支队伍,按从 0 到 n - 1 编号。每支队伍也是 有向无环图(DAG) 上的一个节点。
给你一个整数 n 和一个下标从 0 开始、长度为 m 的二维整数数组 edges 表示这个有向无环图,其中 edges[i] = [ui, vi] 表示图中存在一条从 ui 队到 vi 队的有向边。
从 a 队到 b 队的有向边意味着 a 队比 b 队 强 ,也就是 b 队比 a 队 弱 。
在这场比赛中,如果不存在某支强于 a 队的队伍,则认为 a 队将会是 冠军 。
如果这场比赛存在 唯一 一个冠军,则返回将会成为冠军的队伍。否则,返回 -1 。
注意
- 环 是形如
a1, a2, ..., an, an+1的一个序列,且满足:节点a1与节点an+1是同一个节点;节点a1, a2, ..., an互不相同;对于范围[1, n]中的每个i,均存在一条从节点ai到节点ai+1的有向边。 - 有向无环图 是不存在任何环的有向图。
示例 1:

输入:n = 3, edges = [[0,1],[1,2]] 输出:0 解释:1 队比 0 队弱。2 队比 1 队弱。所以冠军是 0 队。
示例 2:
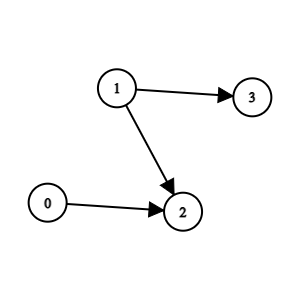
输入:n = 4, edges = [[0,2],[1,3],[1,2]] 输出:-1 解释:2 队比 0 队和 1 队弱。3 队比 1 队弱。但是 1 队和 0 队之间不存在强弱对比。所以答案是 -1 。
思路描述:
这道题能够想到拓扑结构的话,那么也算是一个简单题。
利用拓扑结构,我们定义一个father数组,来存储第i号节点的前驱节点数量,而本题就是要查找的在father数组中前驱节点数量为0的那些编号。
代码:
class Solution {public int findChampion(int n, int[][] edges) {int[] father=new int[n];int m=edges.length;int maxCount=0;int maxIndex=0;for(int i=0;i<m;i++){father[edges[i][1]]++;}for(int i=0;i<n;i++){if(father[i]==0){maxCount++;maxIndex=i;}}if(maxCount==1){return maxIndex;}return -1;}
}这篇关于力扣2923、2924.找到冠军I、II---(简单题、中等题、Java、拓扑排序)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





