本文主要是介绍机器学习和深度学习--李宏毅(笔记与个人理解)Day9,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Day9 Logistic Regression(内涵,熵和交叉熵的详解)
中间打了一天的gta5,图书馆闭馆正好+npy 不舒服那天+天气不好,哈哈哈哈哈总之各种理由吧,导致昨天没弄起来,今天补更!
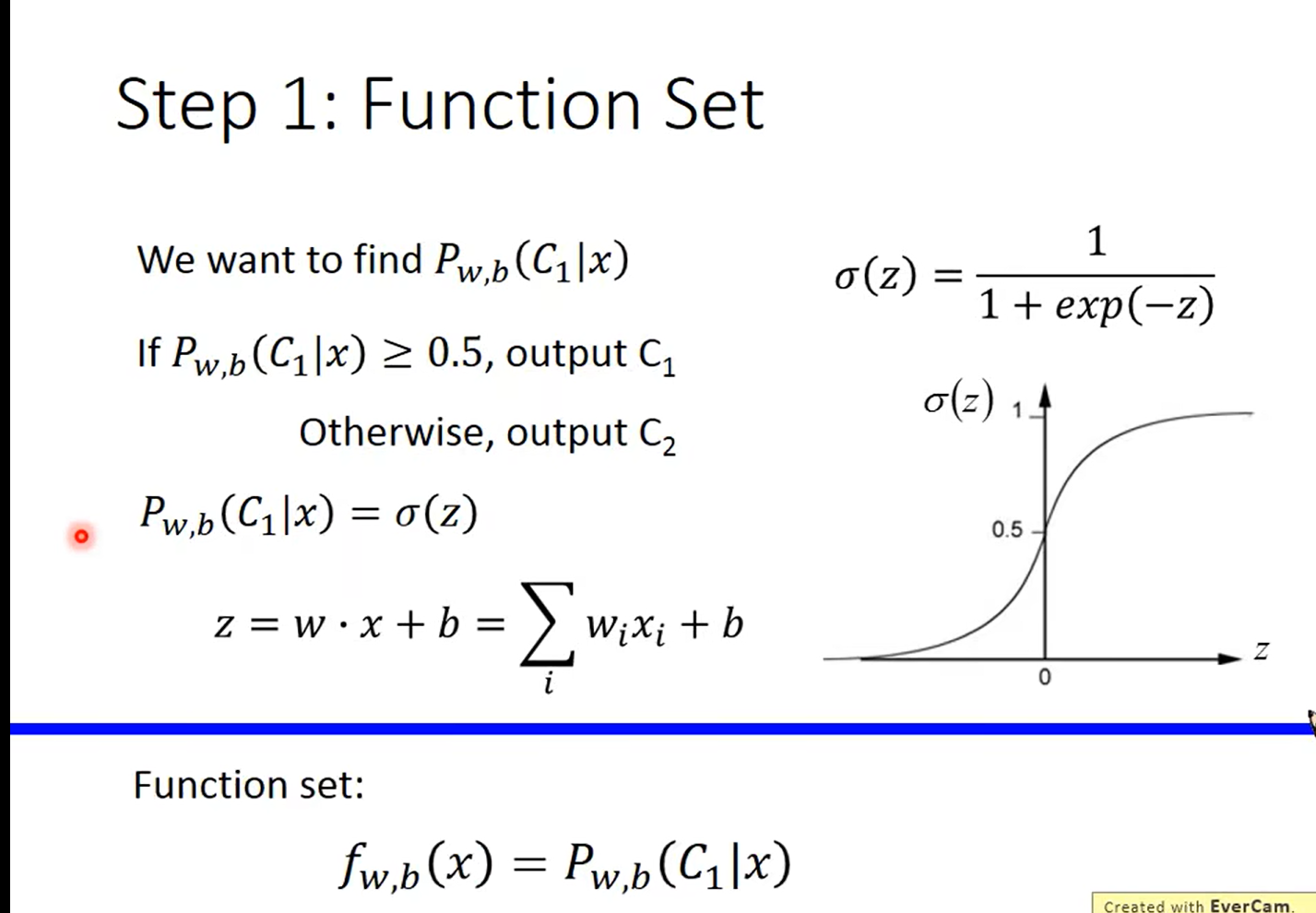
这里重点注意一下, 这个 output值是概率哈,也就是说式子整体表示的含义是 x 属于c1的概率是多大
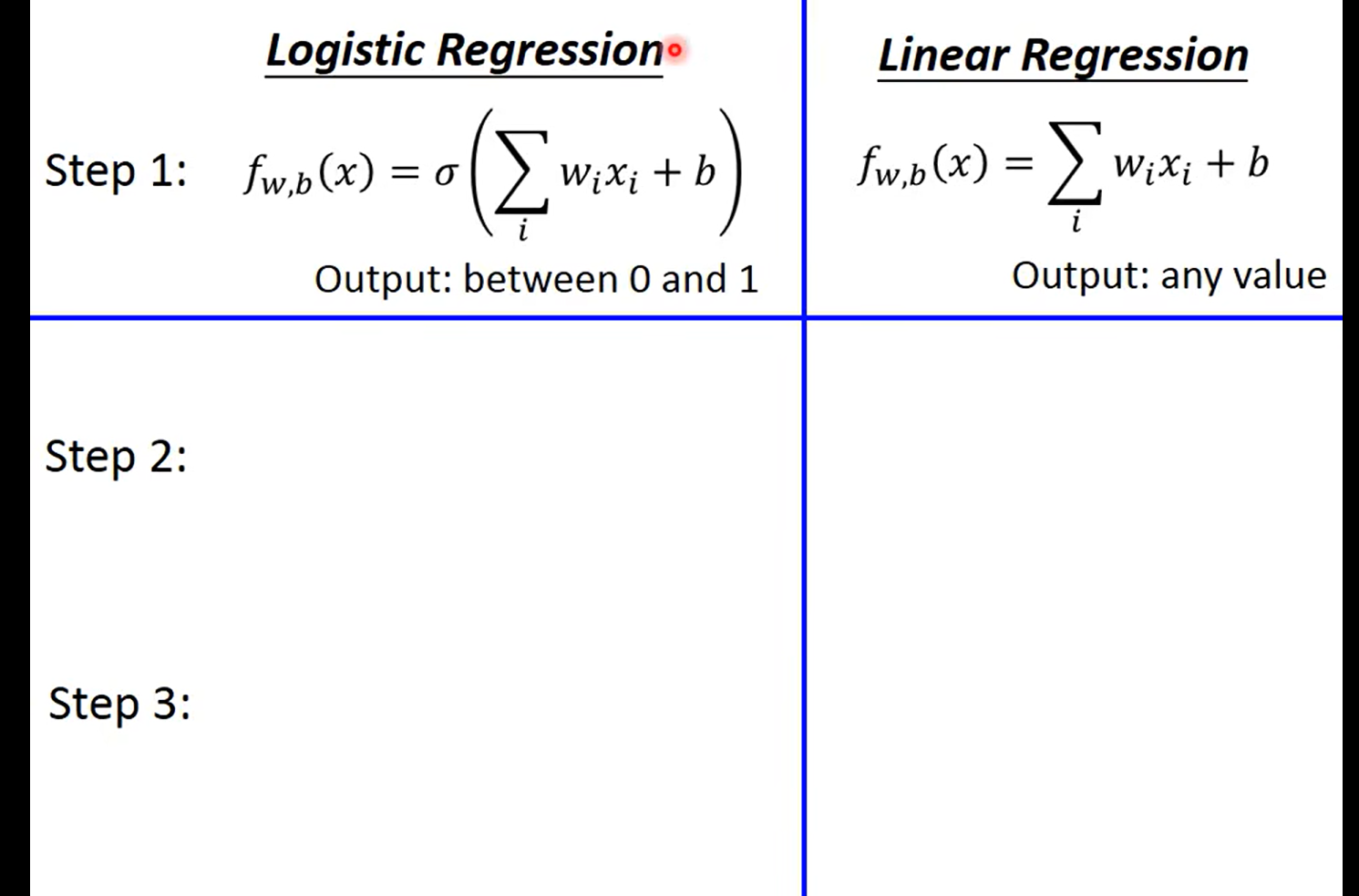
这个老师真的是讲到我的心坎子里区了,这个logistic Redression 和linear Regression 长得真的好像啊,我自己正有疑惑怎么区分,then……
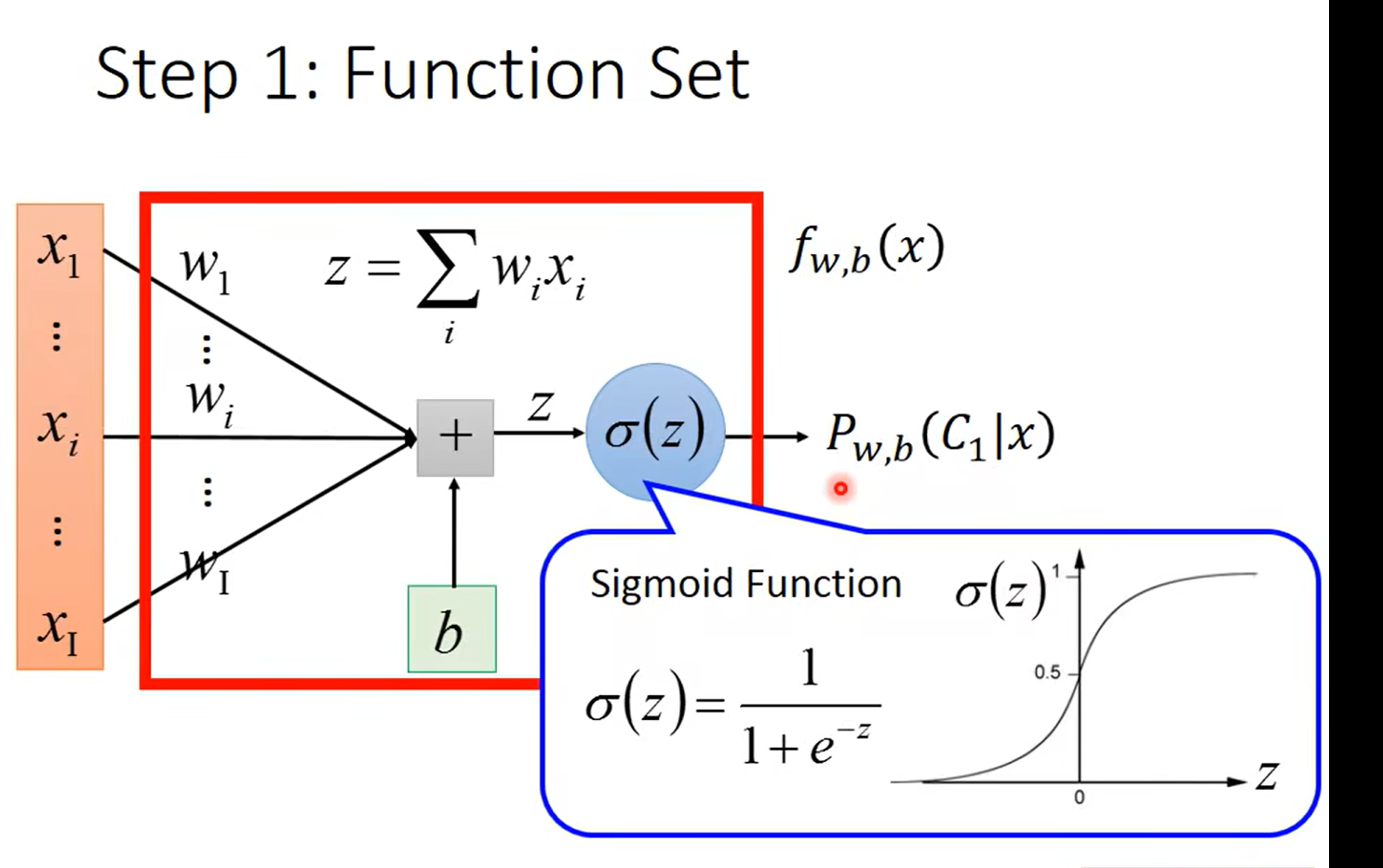
不知道你们看到这里在想什么哈,反正我的第一个反应就是,woc这logisticRegression不是长得和之前的全连接神经网络的神经元一毛一样吗?甚至还是加上了激活函数,sigmoid的

这里就只有概率论的知识哈,这里为什么是1-f(x3 )? 我自己想的话是因为这个回归只回归 C1 的情况,或者说,对于不同的类要做一个处理后,再进行回归

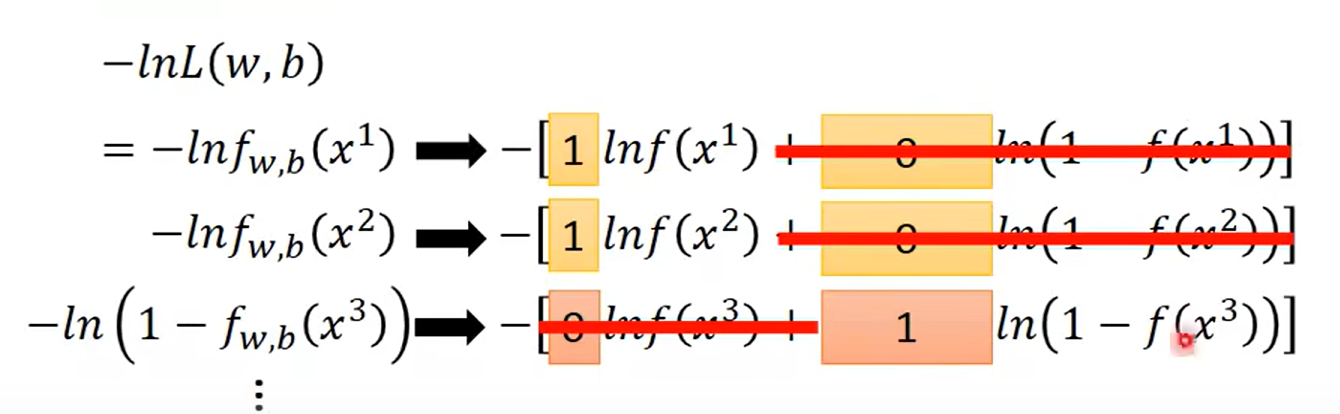
比较巧妙的使用 01 关系来表示了不同的类的回归情况(注意这里不是做分类任务哈, 不要看见class1 啥的就说是分类任务, 敲黑板,看我们的title 是什么?!)

cross Entropy
这里又出现了,cross Entropy的概念,逃不掉了……那就捡起来补一补:
**熵和交叉熵 **:
从信息传递的角度来看:
信息论中熵的概念首次被香农提出,目的是寻找一种高效/无损地编码信息的方法:以编码后数据的平均长度来衡量高效性,平均长度越小越高效;同时还需满足“无损”的条件,即编码后不能有原始信息的丢失。这样,香农提出了熵的定义:无损编码事件信息的最小平均编码长度。
so, how we get this coding length ?( more deeper :何来的最小,又何来的平均呢?)
eg: 假设我考研的地方有四种可能,然后我要把这个秘密的消息传递给我的亲人
编码方式/事件 北京 60% 四川 20% 天津 15% 其他 5% 平均编码长度 方式1 0 1 10 11 1 * 0.6+1 * 0.2+ 2 * 0.15 +2* 0.05 = 1.2 方式2 0 1 111 110 …… 方式3 11 10 0 1 2 * 0.6+2 * 0.2+ 1 * 0.15 +1* 0.05 = 1.75 我们通过计算可以看到,方式1 的平均编码长度是最小的;(这里又想到学c的时候学到的 哈夫曼树,细节上还是有很大不同,由于它用到了树的结构,并不能完全灵活的得到最小编码举例: asdfgh 六个字母,编码出来的最长编码有1001 等,如果直接进行编码 则0 1 10 11 100 101 110,最长仅有3);那么最小编码长度就是,大于N(事件情况)的2的最小次方 ,然后按照出现概率递减依次递增编码;那么计算平均最小长度,(ps:我是真nb,这个小的推导过程我先自己想的,网上一验证发现还真的对了我去)也就是熵的公式为:
熵的直观解释:
那么熵的那些描述和解释(混乱程度,不确定性,惊奇程度,不可预测性,信息量等)代表了什么呢?
如果熵比较大(即平均编码长度较长),意味着这一信息有较多的可能状态,相应的每个状态的可能性比较低;因此每当来了一个新的信息,我们很难对其作出准确预测,即有着比较大的混乱程度/不确定性/不可预测性。
并且当一个罕见的信息到达时,比一个常见的信息有着更多的信息量,因为它排除了别的很多的可能性,告诉了我们一个确切的信息。在天气的例子中,Rainy发生的概率为12.5%,当接收到该信息时,我们减少了87.5%的不确定性(Fine,Cloudy,Snow);如果接收到Fine(50%)的消息,我们只减少了50%的不确定性。
交叉熵
卧槽我一下子就懂了,我tmd 简直就是个天才哈哈
这样想:熵的定义 是该分布下的最小长度;上面那个公式有两个部分我们现在确定不了,p(x)的分布和 需要编码的长度;其实我们做一个预测的时候是啥也不知道的,但是这样不就没法算了嘛,我们不妨假设P(x)是我们知道的,也就是真实的值,那么剩下的编码长度就是观测值咯log2(Q(x)),那么由于Entropy的定义, 是p(x)分布下的最小长度的编码,就不可能出现比这个编码更小的数,所以交叉熵越小,说明我们越接近p(x)分布下的最小长度的编码。(也就解释了,机器学习分类算法中,我们总是最小化交叉熵的之前的疑问)
定义这玩意儿的人也是个天才md


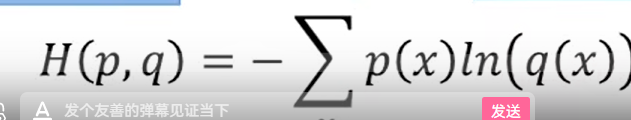
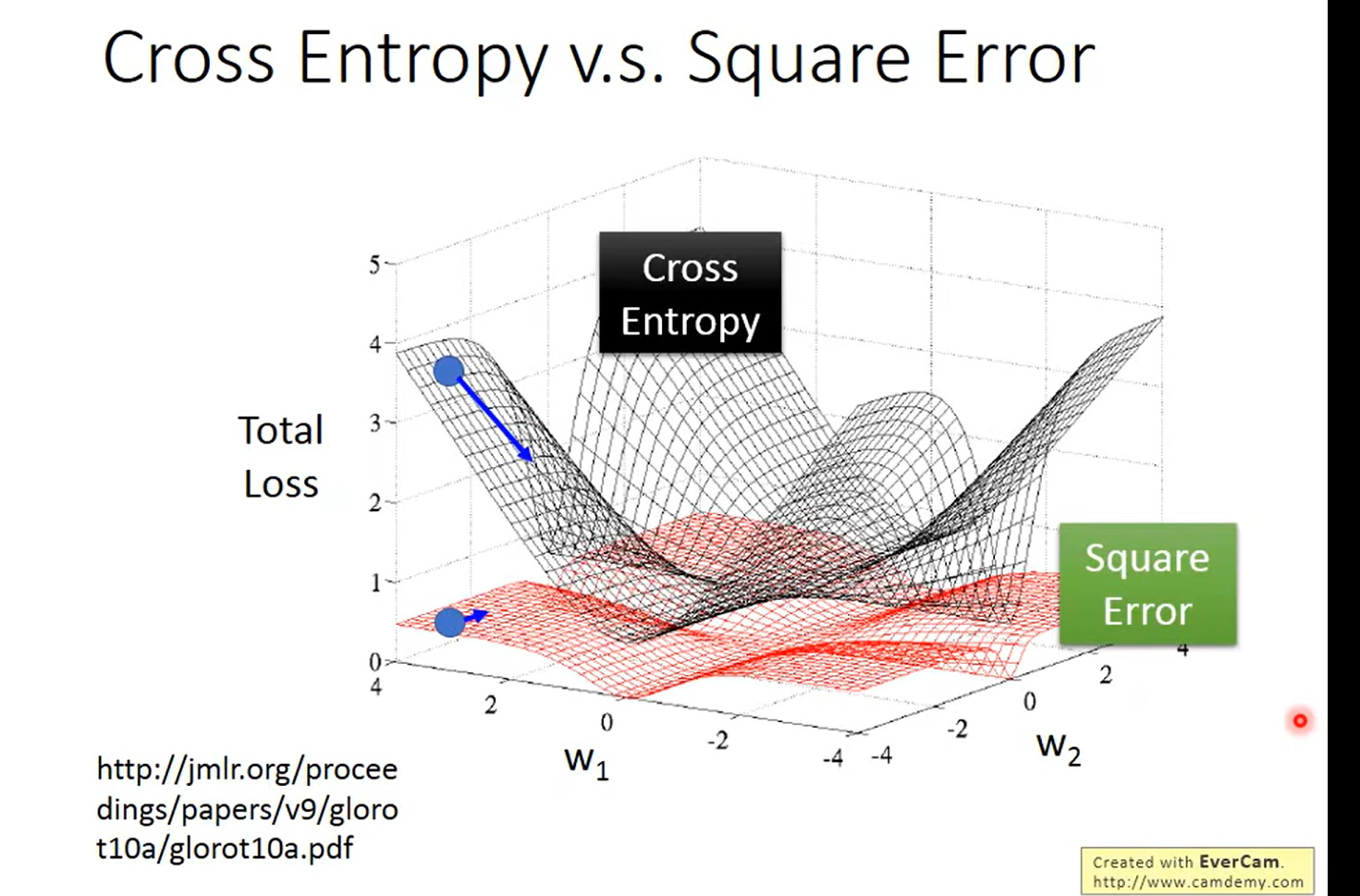
感觉这里老师讲错一个东西, 当这两个函数一模一样的时候 得到的不应该是0 吧


之前我就 是这么做的笑死,直接被当反面教材
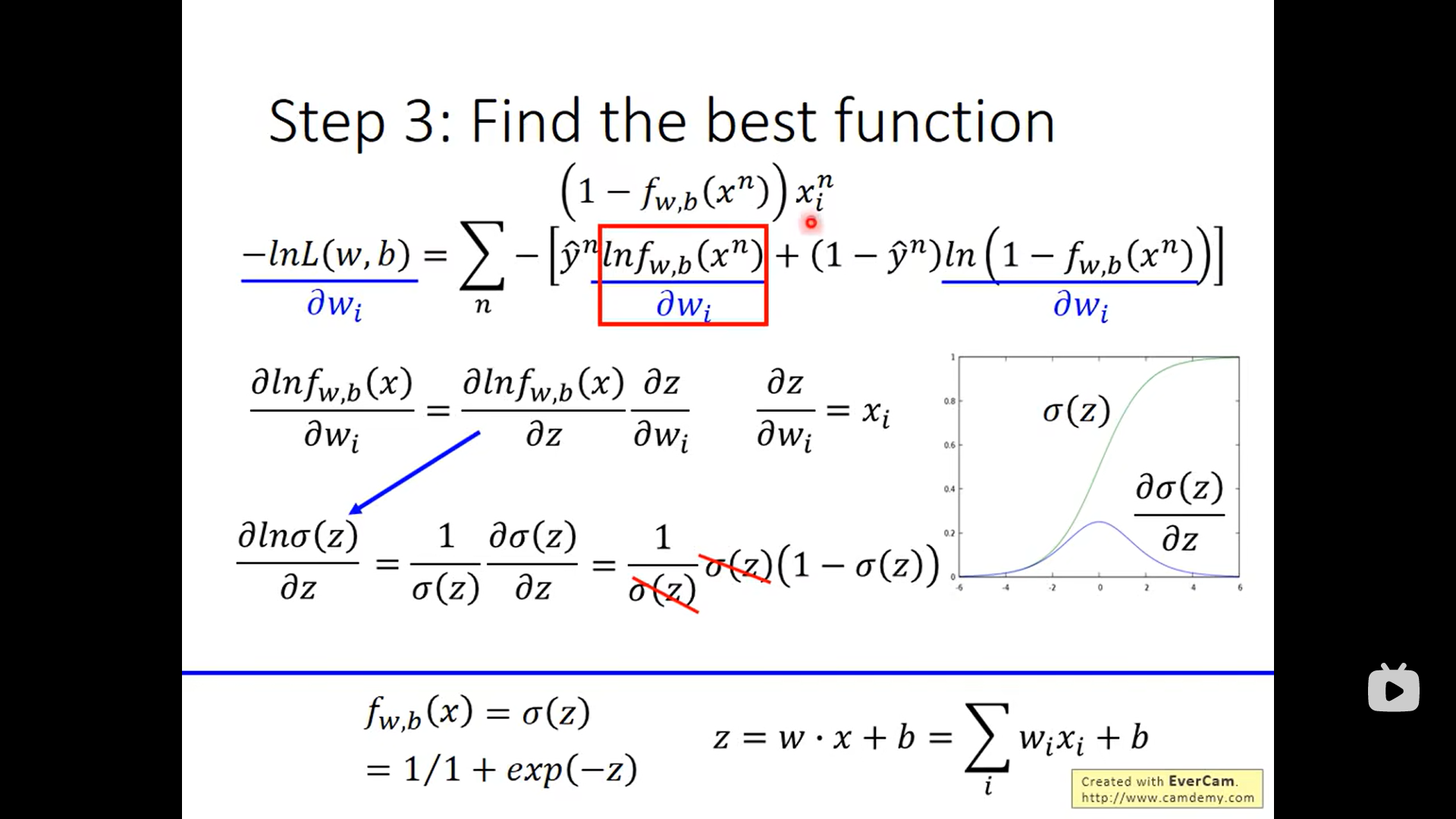

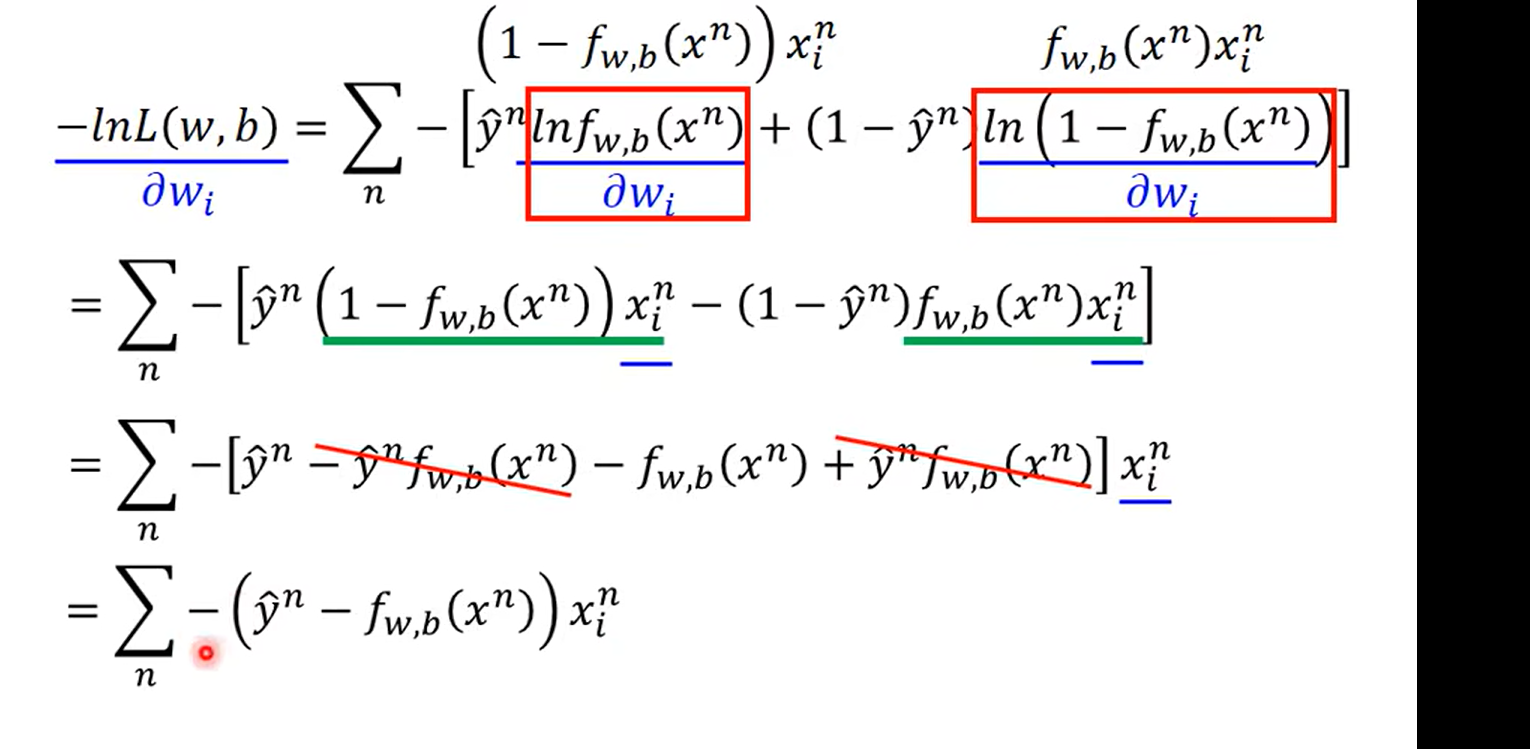
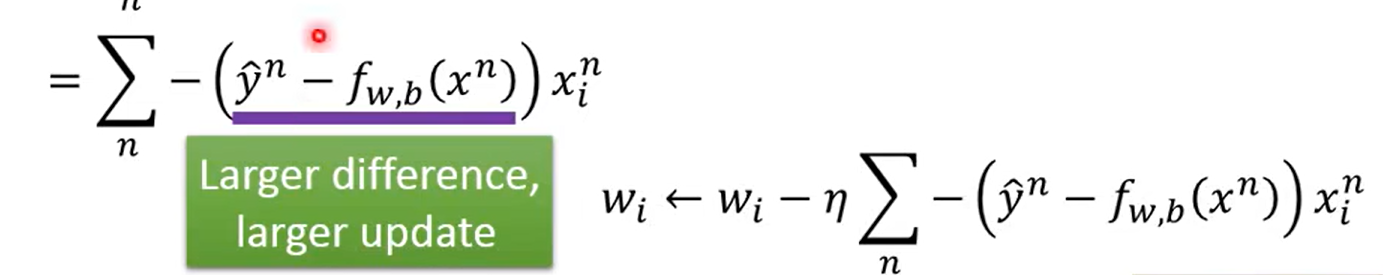
这里有一点小疑问,为什么不是 学习率×这里的w的变化率 ?

NB chatgpt 上大分,这里就是✖ 那个求和符号管的是后面,这个应该就是见的比较少,所以才有疑问

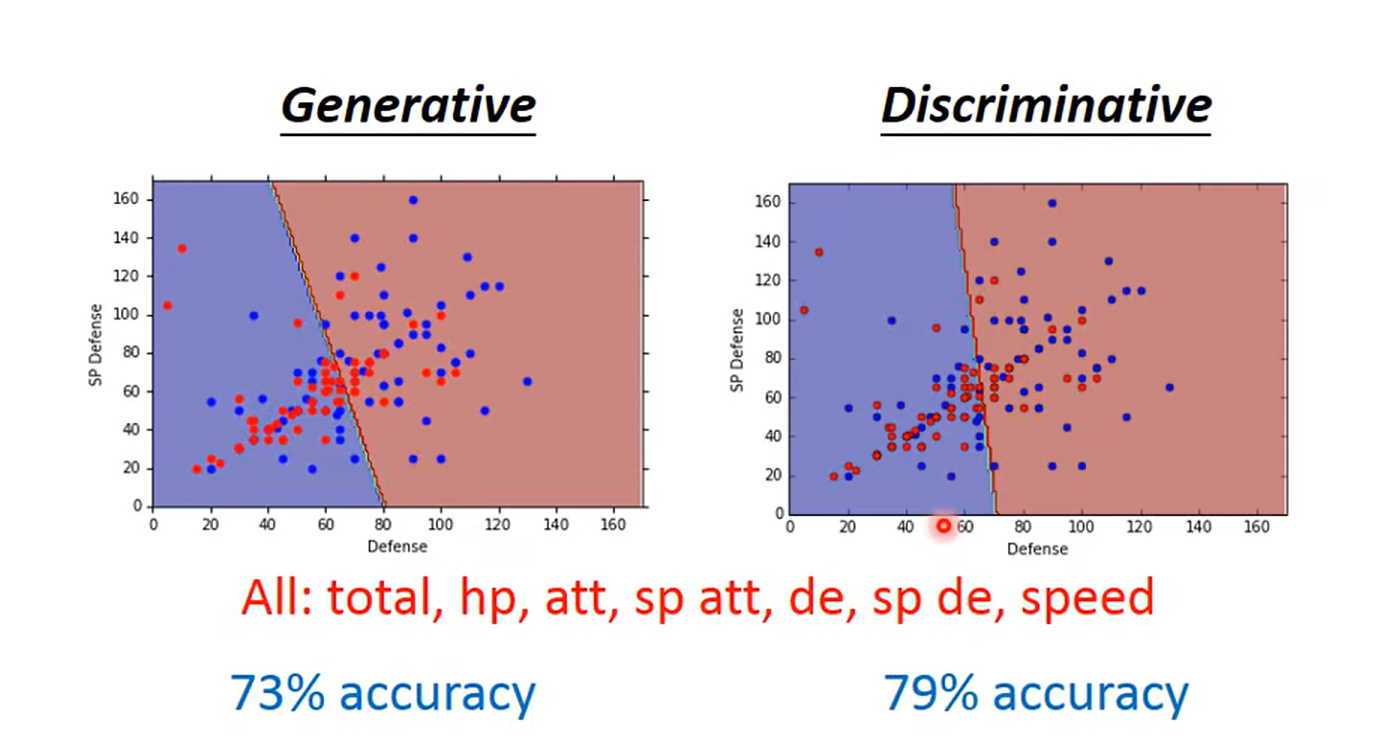
Discriminative VS Generative

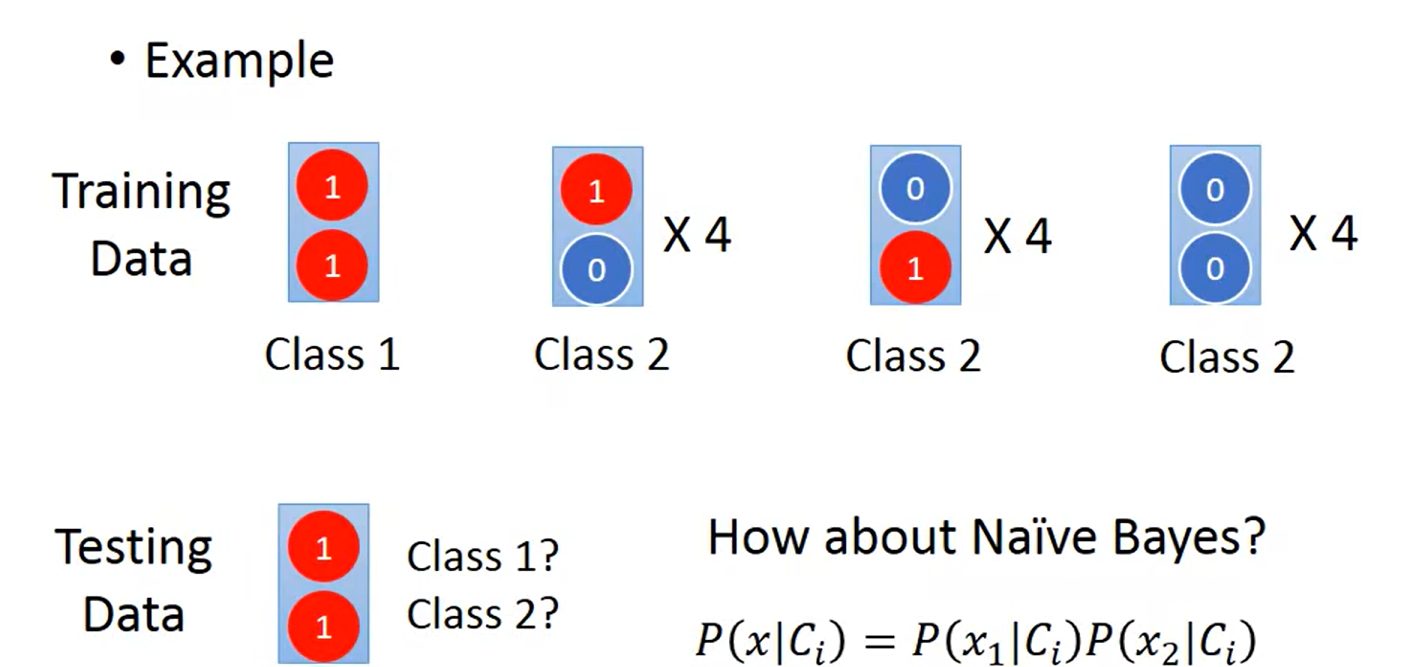

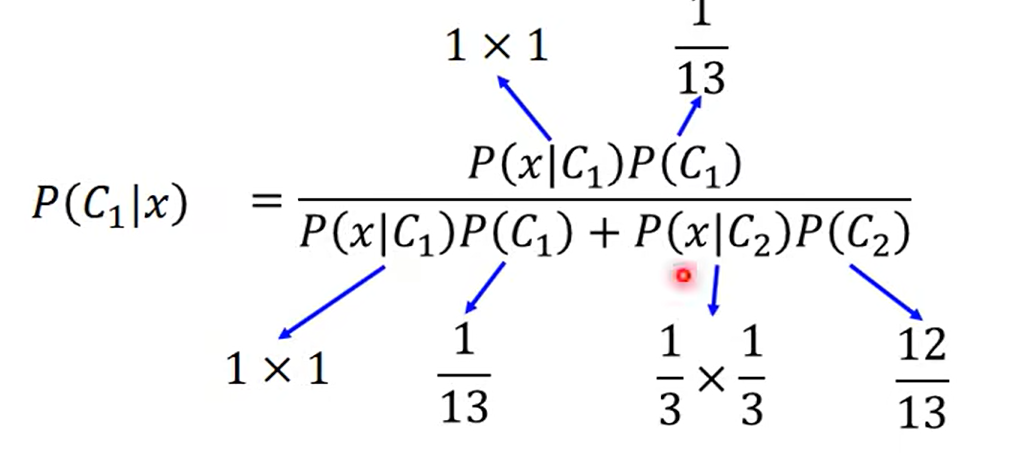
< 0.5
Generative 做了一些假设,脑补了一些数据;这个例子朴素贝叶斯 认为 没有产生11 是因为 sampling的不够多

Multi-class classification
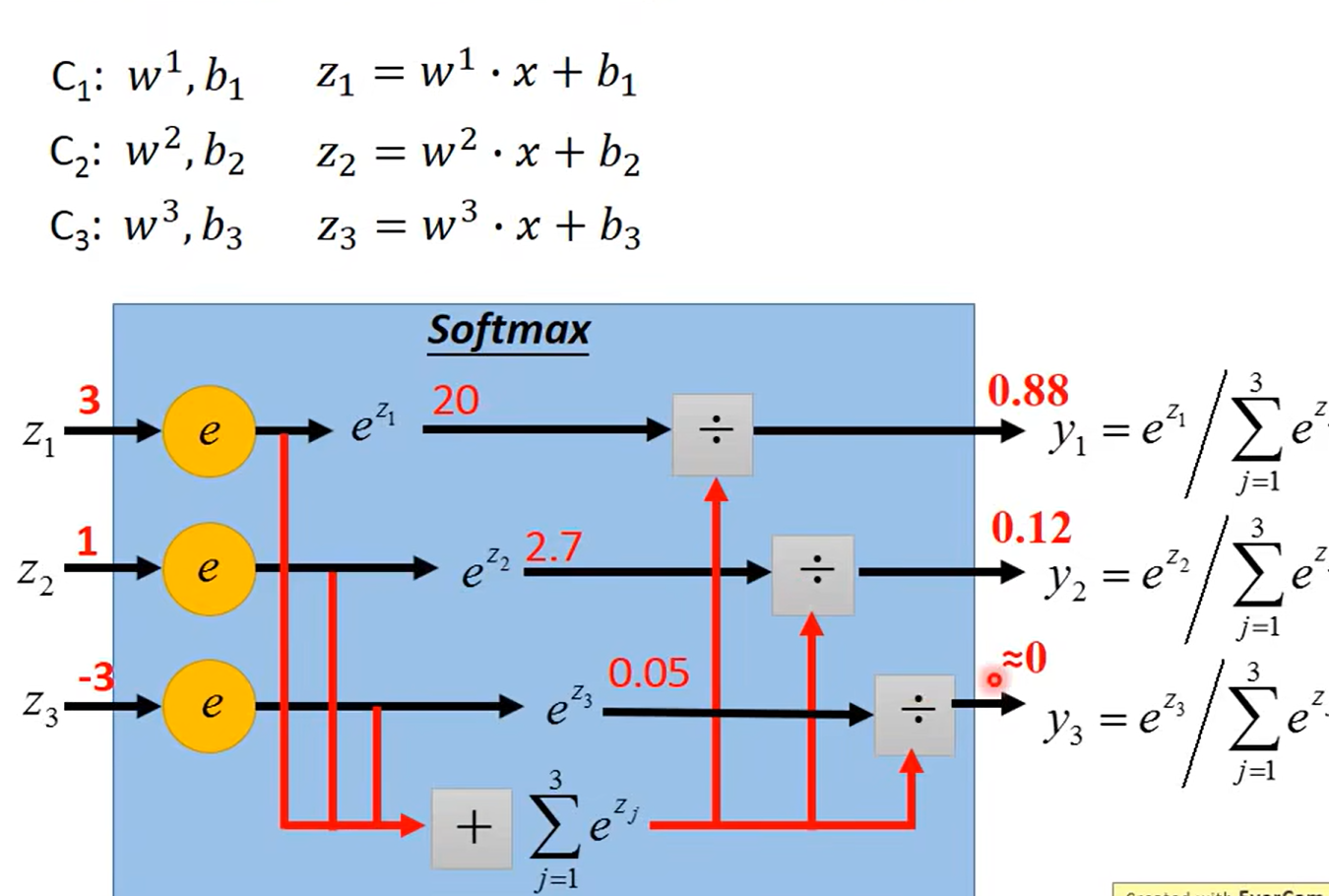
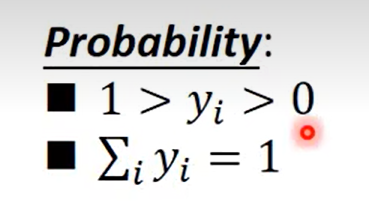
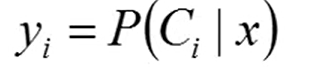
概率或者信息论的角度可以解释
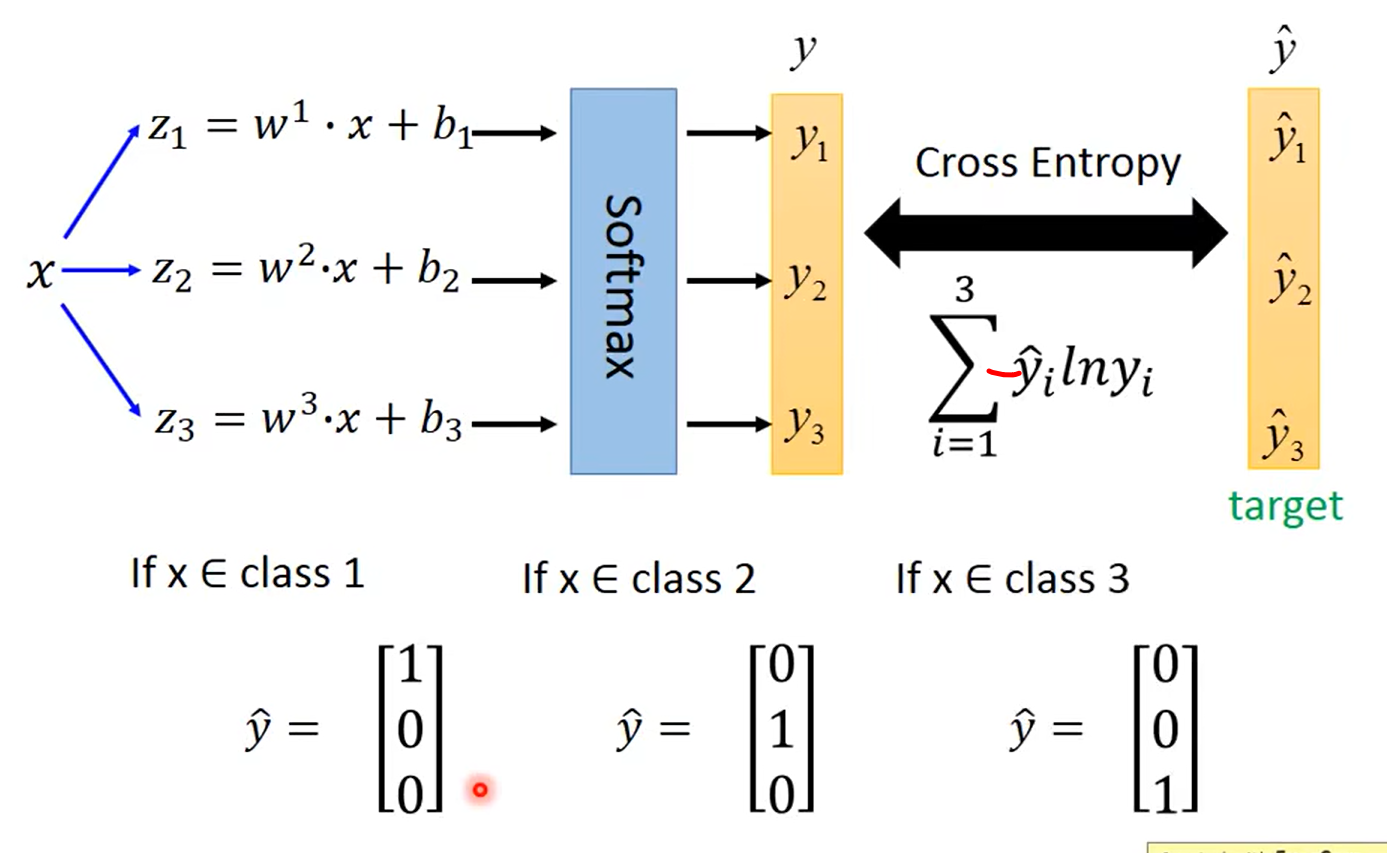
这样编码为什么就没有 关于某几个类之间更近的问题了?
这是一个独热编码(one-hot encoding)的例子。例如,如果有三个类别,那么第一个类别表示为100,第二个类别表示为0,1,0,第三个类别表示为0,0,1。这种编码方式确保了每个类别之间的“距离”是相同的,因为它们在高维空间中是正交的。
Limitation of Logistic Regression
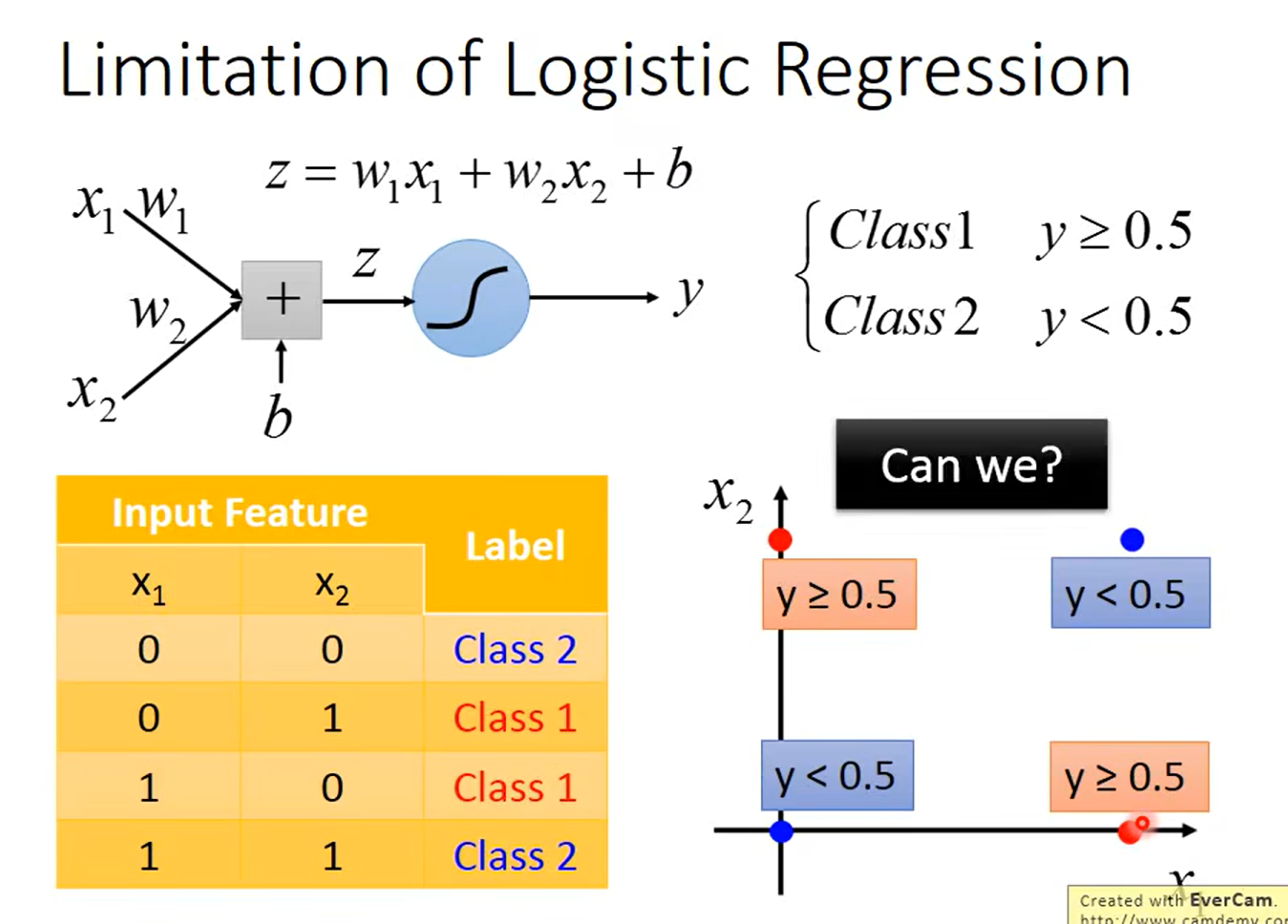
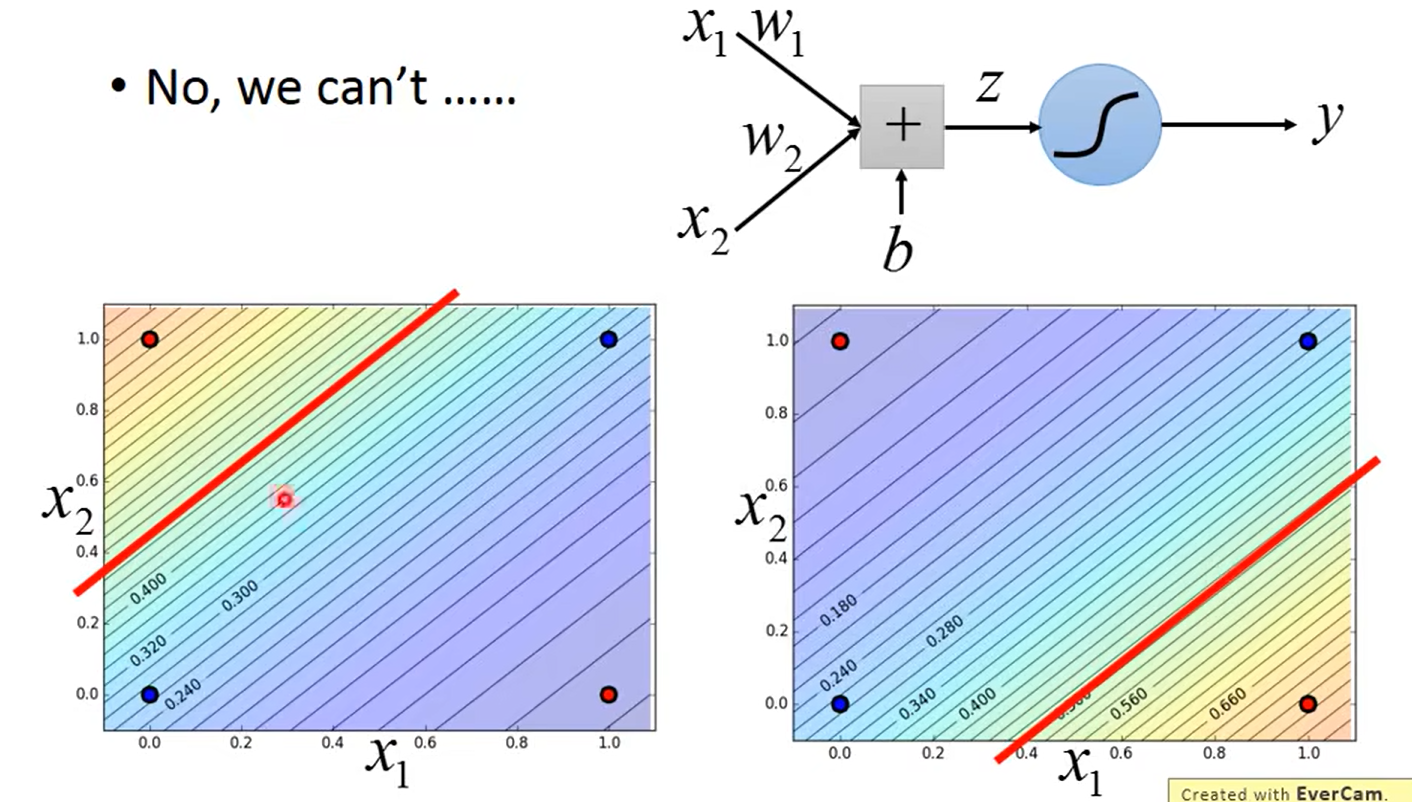
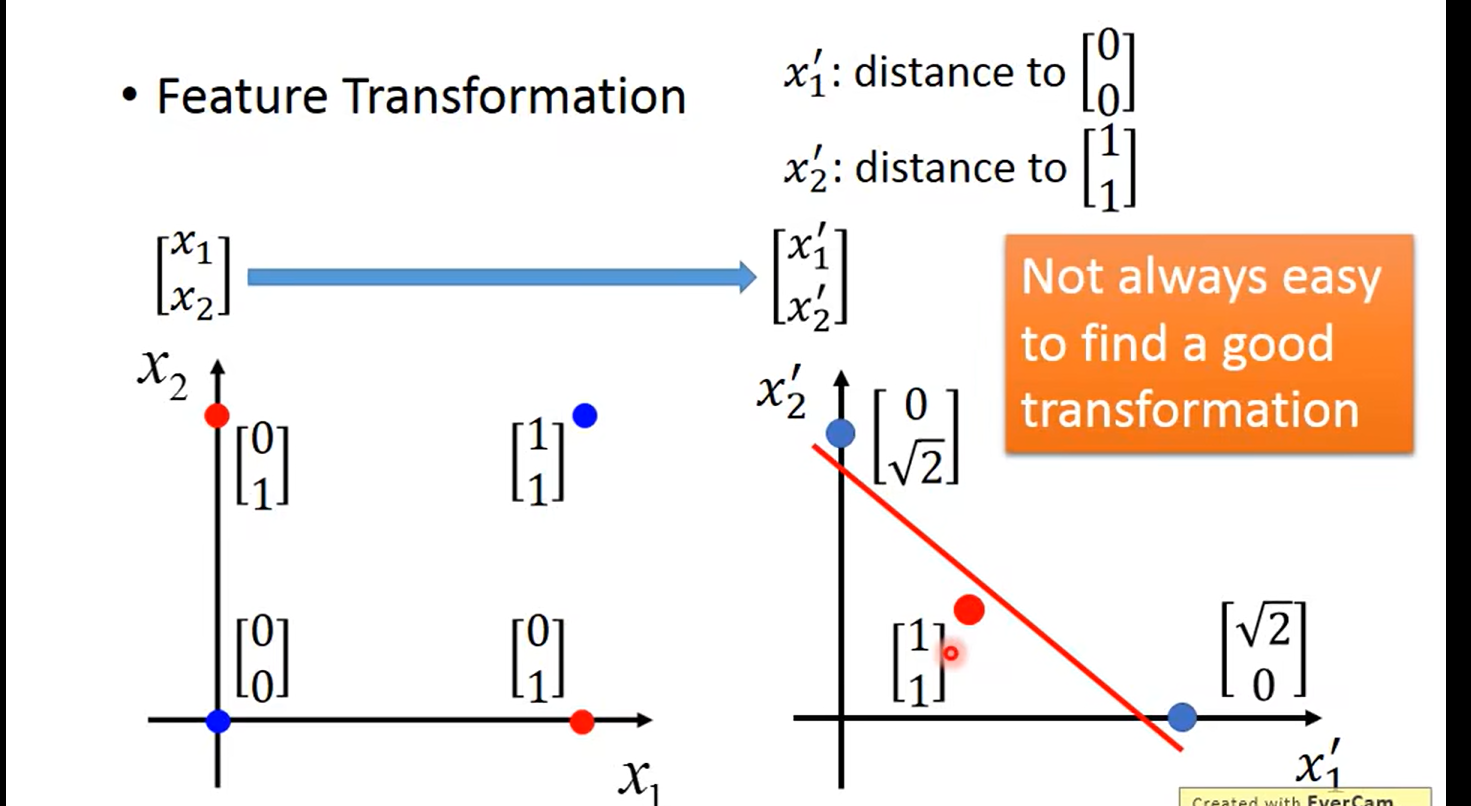
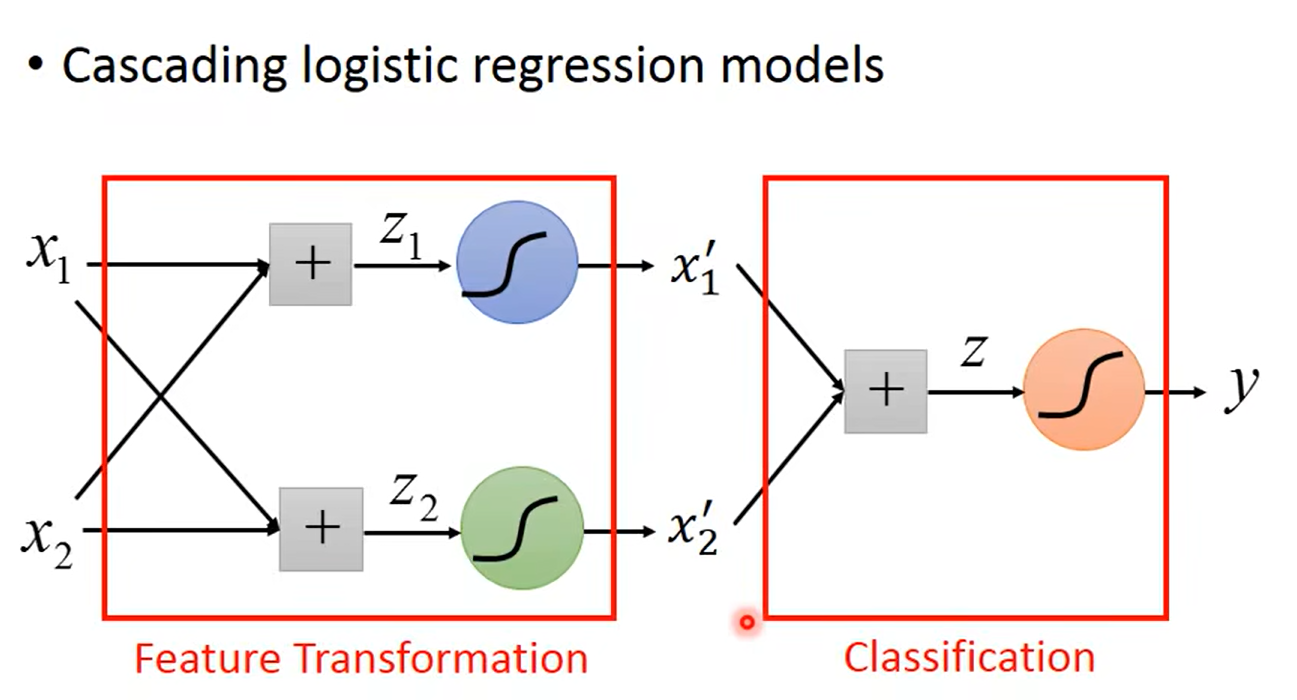
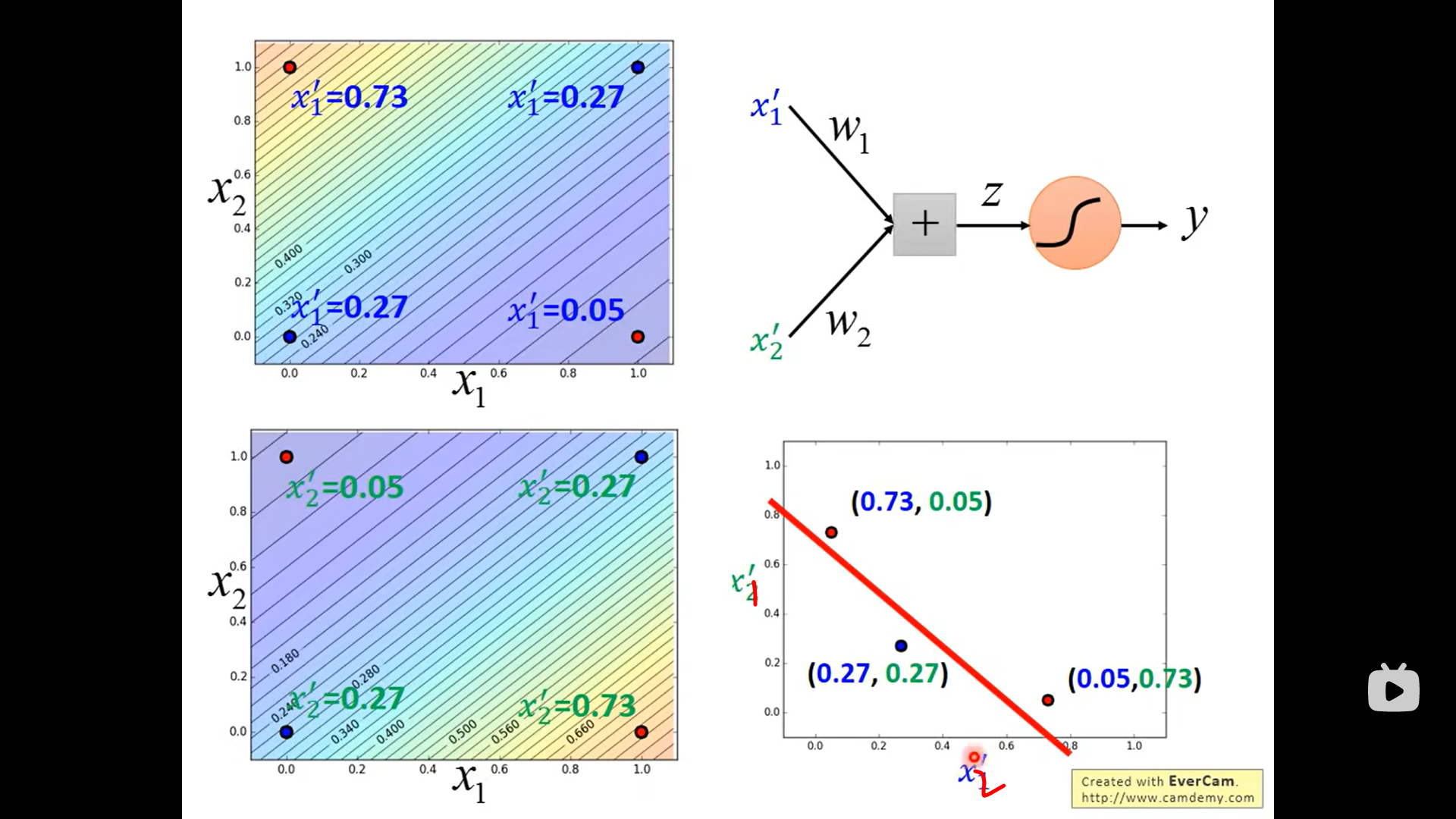
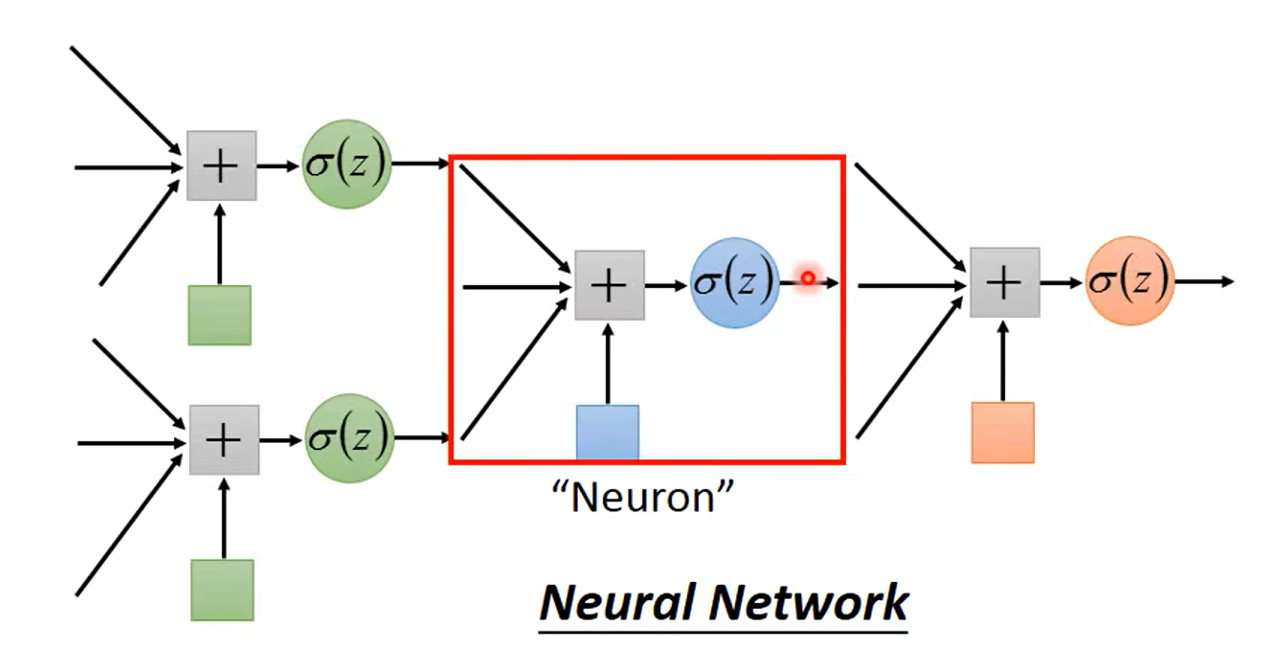
引出 类神经网络 deepLearning
这篇关于机器学习和深度学习--李宏毅(笔记与个人理解)Day9的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!