本文主要是介绍【图论】图的存储--链式前向星存图法以及深度优先遍历图,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
图的存储
介绍
无向图-就是一种特殊的有向图->
只用考虑有向图的存储即可
有向图
- 邻接矩阵
- 邻接表
邻接表
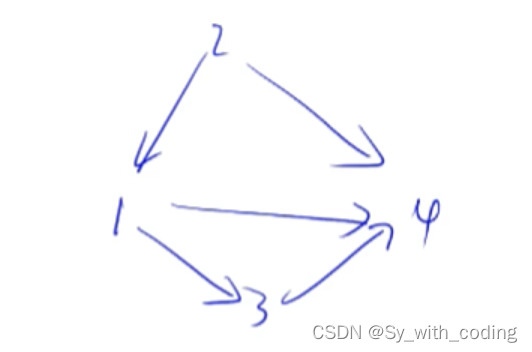
存储结构:
(为每一个点开了一个单链表,存储这个点可以到达哪个点)
1:3->4->null2:1->4->null3:4->null4:null
插入一条新的边
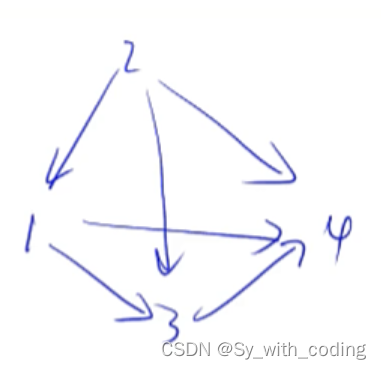
比如要插一条边:
2->3
- 先找到
2对应的单链表 - 然后将
3插入到单链表里面去(一般使用头插)
对应的结构变化为:
- 1:
3->4->null - 2:
3->1->4->null - 3:
4->null - 4:
null
插入边 Coding Part
#include <iostream>
#include <cstring>
#define p(e) print(e, sizeof(e)/sizeof(int))
using namespace std;const int N = 100010, M = N * 2;
//N表示结点数量上限,M表示结点数值上限int h[N], e[M], ne[M], idx;//插入一个a->b
inline void add(int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx++;/** idx是没有使用的空结点索引* 先给这个位置赋值b # e[idx] = b* 然后让这个结点指向头结点 # ne[idx] = h[a]* 然后再更新头结点 # h[a] = idx++* 同时让idx移动到新的空结点索引中去 # idx++*/
}inline void print(int arr[], int n) {for (int i = 0; i < n; i++) cout << arr[i] << ' ';cout << endl;
}int main() {memset(h, -1, sizeof h);
}
遍历图
深度优先方法遍历图
- 需要使用一个
bool数组存放是否遍历的状态 - 然后进行深度优先遍历
#include <iostream>
#include <cstring>using namespace std;const int N = 100010, M = N * 2;
//N表示结点数量上限,M表示结点数值上限int h[N], e[M], ne[M], idx;
bool st[N];
//插入一个a->b
inline void add(int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx++;/** idx是没有使用的空结点索引* 先给这个位置赋值b # e[idx] = b* 然后让这个结点指向头结点 # ne[idx] = h[a]* 然后再更新头结点 # h[a] = idx++* 同时让idx移动到新的空结点索引中去 # idx++*/
}inline void dfs(int u) {st[u] = true;cout << u << ' ' ;for (int i = h[u]; i != -1; i=ne[i]) {int j = e[i];if (!st[j]) dfs(j);}
}int main() {memset(h, -1, sizeof h);memset(st, false, sizeof st);add(1, 3);add(3, 5);add(3, 6);add(1, 2);add(1, 8);dfs(1);
}
题目:树的重心
给定一棵树,树中包含n个结点,(编号为1~n)和n-1个无向边
请找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个结点删除后,剩余各个连通块中点数的最大值最小,那么这个结点被称为树的重心。
输入格式:
第一行包含整数 n,表示树的结点数。
接下来 n-1 行,每行包含两个整数 a 和 b,表示 a 和 b 之前存在的一条边。
输出格式:
输出一个整数 m,表示重心的所有子树中最大子树的结点数目。
数据范围:
1 <= n <= 105
输入样例:
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出样例:
4
答案代码:
#include <iostream>
#include <cstring>using namespace std;const int N = 100001, M = N*2;
int h[N], e[M], ne[M], idx;
bool st[N];//a->b
void add(int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}/*遍历模板*/
void dfs_template(int u) {st[u] = true;cout << u << ' ';for (int i = h[u]; i != -1; i = ne[i]) {int j = e[i];if (!st[j]) {dfs_template(j);}}
}int n; //n为题目输入的结点数量
int ans = INT_MAX; //初始化题目要求的最小值
int dfs(int u) {//每一棵树找到最大连通块的数量st[u] = true;int sum = 1, res = 0; //sum统计子结点(包括自己)的数量, res统计儿子树最大连通块数量for (int i = h[u]; i != -1; i = ne[i]) {int j = e[i];if (!st[j]) {int s = dfs(j);sum += s; //加上子节点的数量res = max(s, res); //找到子树中的最大连通块}}res = max(res, n-sum); //和父亲树进行比较ans = min(ans, res); //更新答案return sum;
}int main() {memset(h, -1, sizeof ne);cin >> n;for (int i = 0; i < n-1; i++) {int a, b;cin >> a >> b;add(a, b), add(b, a);}dfs(1);cout << ans << endl;
}
宽度优先方法遍历图
补充两个图论的概念:
- 重边: 例如,存在两条
1->2的边,叫重边 - 自环:例如,
1->1叫自环
题目:图中点的层次
这篇关于【图论】图的存储--链式前向星存图法以及深度优先遍历图的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





