蓝桥杯刷题-13-子矩阵-二维滑动窗口 ಥ

蓝桥杯刷题-13-子矩阵-二维滑动窗口 ಥ_ಥ

本文主要是介绍蓝桥杯刷题-13-子矩阵-二维滑动窗口 ಥ_ಥ，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在这里插入图片描述
给定一个 n × m （n 行 m 列）的矩阵。
设一个矩阵的价值为其所有数中的最大值和最小值的乘积。求给定矩阵的所有大小为 a × b （a 行 b 列）的子矩阵的价值的和。
答案可能很大，你只需要输出答案对 998244353 取模后的结果。
在这里插入图片描述

//四层for循环
for(){//行nfor(){//列mfor(){//afor(){//b}}}}

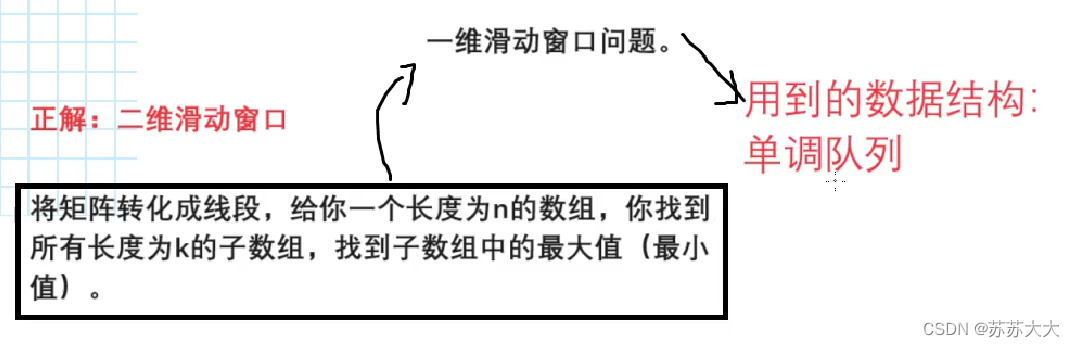
在这里插入图片描述

//二维单调队列
#include<bits/stdc++.h>
#define endl '\n'
#define deb(x) cout << #x << " = " << x << '\n';
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
const int mod =  998244353;
const int N = 1e3 + 10;
int g[N][N];
int q[N];
int line_max[N][N], line_min[N][N];
int maxv[N][N], minv[N][N];
int a, b, n, m;void solve()
{cin >> n >> m >> a >> b;for(int i = 0; i < n; i ++)for(int j = 0; j < m; j ++)cin >> g[i][j];//求出每一行的滑动窗口for(int i = 0; i < n; i ++){int h = 0, t = -1;for(int j = 0; j < m; j ++){if(h <= t and q[h] < j - b + 1){h ++;}while(h <= t and g[i][q[t]] <= g[i][j])t--;q[++t] = j;if(j - b + 1 >= 0){line_max[i][j - b + 1] = g[i][q[h]];}}}//对每一行的滑动窗口求一遍滑动窗口for(int j = 0; j < m; j ++){int h = 0, t = -1;for(int i = 0; i < n; i ++){if(h <= t and q[h] < i - a + 1){h ++;}while(h <= t and line_max[q[t]][j] <= line_max[i][j])t --;q[++t] = i;if(i - a + 1 >= 0)maxv[i - a + 1][j] = line_max[q[h]][j];}}//求最小值//先针对每一行，求出每一行的滑动窗口。for(int i = 0; i < n; i ++){int h = 0, t = -1;for(int j = 0; j < m; j ++){if(h <= t and q[h] < j - b + 1){h ++;}while(h <= t and g[i][q[t]] >= g[i][j])t --;q[++ t] = j;if(j - b + 1 >= 0)line_min[i][j - b + 1] = g[i][q[h]]; }}//针对每一列的滑动黑窗口，求滑动窗口。for(int j = 0; j < m; j ++){int h = 0, t = -1;for(int i = 0; i < n; i ++){if(h <= t and q[h] < i - a + 1){h ++;}while(h <= t and line_min[q[t]][j] >= line_min[i][j])t --;q[++ t] = i;if(i - a + 1 >= 0)minv[i - a + 1][j] = line_min[q[h]][j];}}int ans = 0;for(int i = 0; i < n; i ++){for(int j = 0; j < m; j ++){ans = (ans + maxv[i][j] * minv[i][j] % mod) % mod;}}cout << ans << endl;}signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;t = 1;//cin >> t;while(t--)solve();
}