本文主要是介绍蓝桥杯第十届c++大学B组详解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1.组队
2.年号字符
3.数列求值
4.数的分解
5.迷宫
6.特别数的和
7.完全二叉树的权值
8.等差数列
9.后缀表达式
10.灵能传输
1.组队
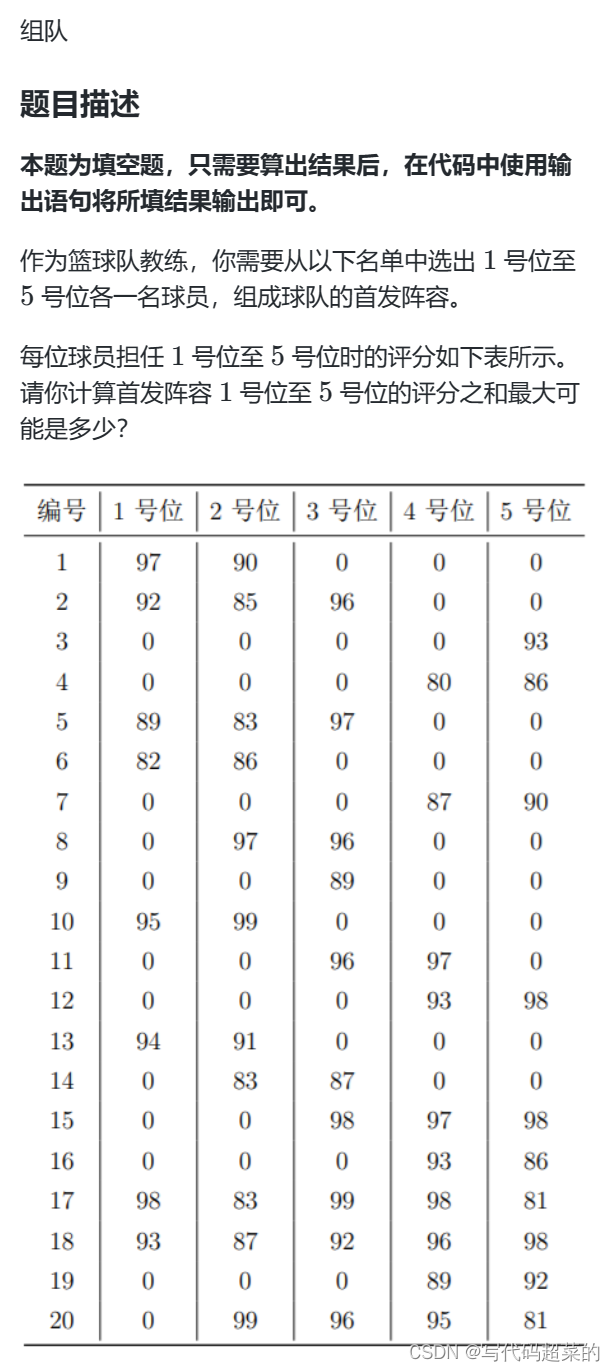
题目解析:就是在个篮球人中选择这个最大的成绩,每个人只能选择一次不能重复选择。选满5人之后的成绩是最大。可以手算也可以使用dfs。直接找到每行最大的然后相加即可。
#include <iostream>
using namespace std;int vis[21];
int a[21][6];
int mmax = 0;void dfs(int p, int sum)
{if(p > 5){if(sum > mmax){mmax = sum;} }else{for(int i = 1; i <= 20; i++){if(vis[i] == 0){vis[i] = 1;dfs(p + 1, sum + a[i][p]);vis[i] = 0;}}}
}int main()
{for(int i = 1; i <= 20; i++){vis[i] = 0;for(int j = 1; j <= 5; j++){cin >> a[i][j];}}dfs(1, 0);cout << mmax << endl;return 0;
}2.年号字符

这个题目和数字逆序有类似的地方。找规律可以得到一下:
27 % 26 == 1;
27 / 26 = 1;
1 % 26 = 1;--> AA;
329 % 26 = 17 Q
329 / 26 = 12
12 % 26 = 12; L ---> LQ
那么2019也可以同意这样进行运算,可以手算也可以写代码。
#include <iostream>
using namespace std;
#include<string>
#include<vector>vector<char> ret(4);
int main()
{int n = 2019;while(n != 0){int t = n % 26;ret.push_back((char)(t + 64));n /= 26;}for(int i = ret.size() - 1; i >= 0; i--){cout << ret[i];}return 0;
}3.数列求值

本题是不是很像斐波那契数列,就是这种思想。
#include <iostream>
using namespace std;int a[20190325] = {0};int main()
{a[0] = 0, a[1] = a[2] = a[3] = 1;for(int i = 4; i <= 20190324; i++){a[i] = (a[i - 1] + a[i - 2] + a[i - 3]) % 10000;}cout << a[20190324] << endl;return 0;
}4.数的分解

题目解析:和第二题有点类似,就是两个任务首先每位进行检查以及不能超过2019,还有重复的问题。那我们就直接从小到大进行检查就不会重复。
#include <iostream>
using namespace std;bool is_true(int x)
{while(x){int t = x % 10;if(t == 2 || t == 4)return false;x /= 10;}return true;
}int main()
{int ans = 0;for(int a = 1; a < 2019; a++){if(is_true(a)){for(int b = a + 1; b < 2019; b++){if(is_true(b)){int c = 2019 - a - b;if(c > b && is_true(c)){ans++;}}}}}cout << ans << endl;return 0;
}5.迷宫

题目解析:本题就是采用动态规划dp,进行上下左右直到走到出口。采用queue来记录结果。
如果没走过并且还不是墙就标记。但是注意是由顺序之分的。
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;#define N 30
#define M 50char map[N][M];
int dir[4][2]={{1,0},{0,-1},{0,1},{-1,0}};//D<L<R<U
char ch[4]={'D','L','R','U'};
int vis[N][M]={0};struct point
{int x,y;string road;point(int a,int b){x=a;y=b;}
};void bfs()
{queue<point> q;point p(0,0);p.road="";q.push(p);vis[0][0]=1;while(!q.empty()){point t=q.front();q.pop();if(t.x==N-1&&t.y==M-1){cout<<t.road<<endl;break;}for(int i=0;i<4;i++){int dx=t.x+dir[i][0];int dy=t.y+dir[i][1];if(dx>=0&&dx<N&&dy>=0&&dy<M){if(map[dx][dy]=='0'&&!vis[dx][dy]){point tt(dx,dy);tt.road=t.road+ch[i];//记录路径q.push(tt);vis[dx][dy]=1;}}}}
}int main()
{for(int i=0;i<N;i++){for(int j=0;j<M;j++)scanf("%c",&map[i][j]);getchar();//读掉回车 }bfs();return 0;
}6.特别数的和

题目解析:是不是觉得这届查重很严重,题目都差不多,和第四题类似。
#include <iostream>
using namespace std;bool check(int x)
{while(x){int t = x % 10;if(t == 2 || t == 0 || t == 1 || t == 9)return true;x /= 10;}return false;
}int main()
{int n;int sum = 0;cin >> n;for(int i = 1; i <= n; i++){if(check(i)){sum += i;}}cout << sum << endl;return 0;
}7.完全二叉树的权值
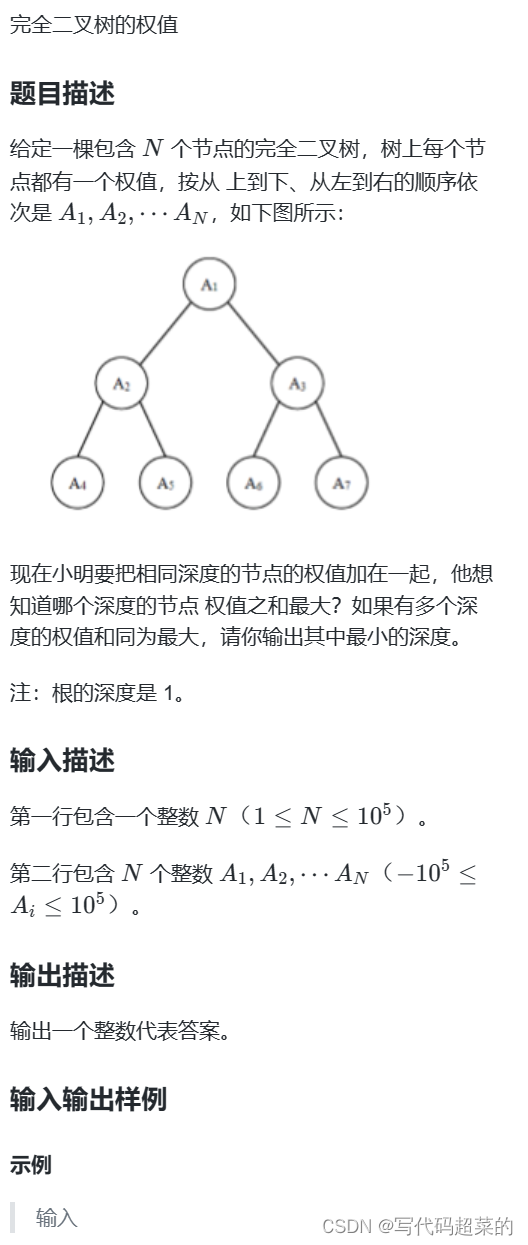
题目解析:
#include <iostream>
#include<cmath>
using namespace std;int a[100005];
int main()
{int N;int deep = 1;int sum = 0;long long max_sum = -10000000000;int max_deep = 1;cin >> N;for(int i = 1; i <= N; i++){cin >> a[i];sum += a[i];//用来每一层的和。if(i == pow(2, deep) - 1){if(max_sum < sum){max_sum = sum;max_deep = deep;}sum = 0;deep++;}}cout << max_deep << endl;return 0;
}8.等差数列

题目解析:要求最小数的等差数列,那么就是尽可能的是输入的数全都是等差数列的项,因为(an-a1) = (n -1)d;
2 6 4 10 20
2 4 6 10 20
它们分别和首项的差:
2 4 8 18;
使得公差最大就是可以留住最多的数列。那么就是求最大公约数。
#include <iostream>
#include <algorithm>using namespace std;const int N = 100010;int n;
int a[N];
int ans;int gcd(int a, int b)
{return b ? gcd(b, a % b) : a;
}int main()
{cin >> n;for (int i = 0; i < n; i++) cin >> a[i];sort(a, a + n);for (int i = 1; i < n; i++)ans = gcd(ans, a[i] - a[0]);if (ans == 0) cout << n << endl;else cout << (a[n - 1] - a[0]) / ans + 1<< endl;return 0;
}9.后序表达式

题目解析:可以分为一下情况:减号数目为0,减号数目不为0的话就有
1.负数数目为0:其他值的相加。2.全是负数,其他绝对值之和再减去最小的数。
3.负数个数大于0小于全部个数。那么就是其他值的绝对值之和。
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;int n, m;
int flag = 0;
int a[200005];
int sum = 0;
int mi = 1000000009;int main()
{cin >> n >> m;for(int i = 0; i < m + n + 1; i++){cin >> a[i];if(a[i] < 0)flag++;sum += a[i];mi = min(mi, a[i]);}if(m == 0){cout << sum << endl;}else{if(flag == 0){cout << (sum - mi) - mi << endl;}else if(flag == m + n + 1){sum = 0; mi = 1000000009;for(int i = 0; i < m + n + 1; i++){sum += abs(a[i]);mi = min(mi, abs(a[i]));}cout << (sum - mi) - mi << endl;}else{for(int i = 0; i < m + n + 1; i++){sum += abs(a[i]);}cout << sum << endl;}}return 0;
}10.灵能传输

题目解析:
举个例子:
a[]:2 3 4 -8
S[]:2 5 9 1
将a[3] ==4进行灵能传输;得到a[]: 2 7 -4 -4; s[]: 2 9 5 1;
仔细观察可以知道就是灵能传输的那一位和前面一位的s[]进行调换。
相反的将s[i]和s[i -1]进行调换那么就是将a[i]进行灵能传输。
那么就是除去s[0]和s[n]两个位置不调换其他都可以调换使得得到的s[i]-s[i-1]最小。
那么要求要递增序列.
#include <bits/stdc++.h>
typedef long long LL;
using namespace std;
int main()
{int t;cin >> t;while (t--) {int n;cin >> n;vector<LL> S(n + 1); for (int i = 0; i < n; i++) {int x;cin >> x;S[i + 1] = S[i] + x;}LL S0 = S[0], Sn = S[n];if (S0 > Sn)swap(S0, Sn);sort(S.begin(), S.end());for (int i = 0; i <= n; i++) { if (S[i] == S0) {S0 = i;break;}}for (int i = 0; i <= n; i++) { if (S[i] == Sn) {Sn = i;break;}}vector<LL> a(n + 1); vector<bool> v(n + 1); int l = 0, r = n;for (int i = S0; i >= 0; i -= 2) { a[l++] = S[i];v[i] = true;}for (int i = Sn; i <= n; i += 2) { a[r--] = S[i];v[i] = true;}for (int i = 0; i <= n; i++) { if (!v[i])a[l++] = S[i];}LL ans = 0;for (int i = 1; i <= n; i++) {ans = max(ans, abs(a[i] - a[i - 1]));}cout << ans << endl;}return 0;
}这篇关于蓝桥杯第十届c++大学B组详解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





