ZYNQ实验--CIC插值滤波器实验

本文主要是介绍ZYNQ实验--CIC插值滤波器实验，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、CIC滤波器介绍

CIC (Cascaded Integrator-Comb) 滤波器是一种常用的数字信号处理滤波器，主要用于降采样（decimation）和升采样（interpolation）操作。它具有简单的硬件实现、高效的运算速度以及适用于需要快速处理的应用场景等优点。半带滤波器具有较好的通带平坦特性,但考虑到面积和功耗,通常只能实现偶数倍的采样率变化。CIC滤波器在信号带宽为8分之一采样率时的滤波效果较好，因此在实际使用中为保证整体滤波的带内平坦和较好的滤波效果，CIC滤波会结合半带滤波器实现高倍采样率变化。

在理论上，多级CIC（Cascaded Integrator-Comb）滤波器可以通过级联多个单级CIC滤波器来实现。然而，根据Noble恒等式的观点，即“先进行抽取或插值，再进行线性滤波”与“先进行线性滤波，再进行抽取或插值”是等价的，我们可以将多个单级CIC滤波器的结构进行变换，可以节省资源并提高计算速度，更为实用。

1.1 CIC滤波器基本结构

CIC滤波器分为3部分：积分器，抽取/插值器，梳状器。本实验在Vivado 2018.3 环境中完成并进行仿真。根据插值滤波器的结构，使用Verilog HDL分别完成积分模块、插值模块、梳状模块的设计。下图分别为CIC抽取和CIC插值滤波器的基本结构图，图中参数：R为抽取或插值系数，M为差分延迟，在工程中一般取1或者2，N为滤波器级数。
在这里插入图片描述

1.2 CIC滤波器位宽确定

上文图中R抽取或插值系数，M差分延迟(M为CIC阶数)，N滤波器级数和Bin输入数据的位宽将决定积分器Bout不发生溢出的位宽值。 计算公式如下：

抽取滤波器
$B_{\operatorname{out}}=\left\lceil N \log _2 R M+B_{in}\right\rceil$
插值滤波器
$B_{\operatorname{out}}=\left\lceil\log _2 \frac{(R M)^N}{R}+B_{in}\right\rceil$
与CIC抽取滤波器不同，插值并不要求所有滤波器有相同的位宽，这里使用的最大位宽公式。

说明： M这个参数有的文章认为是CIC滤波器的阶数，但有的文章计算公式中有M却并为说明M是什么参数并且设计中也没有体现，结合找到的参考资料在本设计中认为M为差分延迟参数，设置为1。CIC抽取滤波可以在中间级进行舍入操作，但是CIC插值滤波不能进行舍入操作，因为积分器在梳状器之后，梳状器引入的量化误差会在积分器中累加引起滤波器的不稳定。

二、CIC插值滤波器实现

2.1位宽确定

实验设计的插值滤波器插值系数 $R = 96 ， M = 1 ， N = 4 ， B in = 16 bi t$ ，根据计算公式得
$B_{\operatorname{out}}=\left\lceil\log _2 \frac{(R M)^N}{R}+B_{in}\right\rceil=\left\lceil\log _2 \frac{(96*1)^4}{96}+16\right\rceil=36bit$
MATLAB的FDATOOL工具观察CIC滤波器的频谱。
在这里插入图片描述

//模块定义
module CIC#(parameter STAGES = 4, // 滤波器阶数parameter DATA_WIDTH = 16, // 数据宽度parameter INDATA_WIDTH = 36, // 中间数据宽度parameter Ntimer = 96 // 插值倍数
)
(input clk_in,  // 输入数据时钟input clk_out, // 输出数据时钟（Ntimer倍于输入数据时钟）input reset,   // 复位信号input signed [DATA_WIDTH-1:0] data_in, // 输入数据output reg signed [DATA_WIDTH-1:0] data_out // 输出数据
);
// 积分器的寄存器
reg signed [INDATA_WIDTH-1:0] integrator [0:STAGES-1]; 
// 梳状器的寄存器
reg signed [INDATA_WIDTH-1:0] comb [0:STAGES-1]; 
reg signed [INDATA_WIDTH-1:0] combd [0:STAGES-1]; 
// 插值的寄存器
reg signed [INDATA_WIDTH-1:0] interpolation = 0;
reg [7:0] cont;
// 输出缓冲
reg signed [INDATA_WIDTH-1:0] output_buffer = 0;// 将输出缓冲的值映射到输出端口
always @(posedge clk_out) begindata_out <= output_buffer[INDATA_WIDTH-1:INDATA_WIDTH-15]; // 可能需要调整以适应实际的位宽和动态范围
endendmodule

2.2 梳状器模块(fs)

// 梳状器（由输入时钟驱动）
always @(posedge clk_in or posedge reset) beginif (reset) beginfor (i = 0; i <STAGES; i = i + 1) begincomb[i] <= 0;combd[i]<= 0;endend else begin//梳状器操作comb[0] <= {{(INDATA_WIDTH-16){data_in[15]}},data_in};for (i = 0; i <STAGES; i = i + 1) begincombd[i] <= comb[i];endfor (i = 1; i <STAGES; i = i + 1) begincomb[i] <= comb[i-1]-combd[i-1];endend
end

一级comb的RTL图，实现输入与输入延时一个单位后相减的操作。
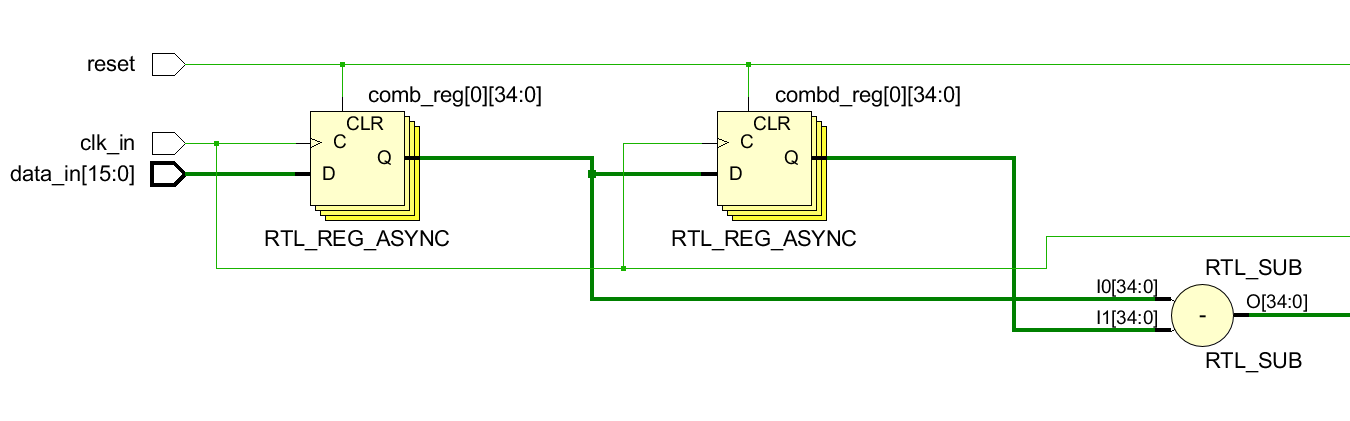
在这里插入图片描述

2.3 插值器模块(N*fs)

对梳状器结果进行插值操作，即间隔N点补零

// 插值器(输出时钟驱动)
always @(posedge clk_out or posedge reset) beginif (reset) begininterpolation <= 0;cont<=0;end else begincont<=cont+1;if(cont==Ntimer-1) begin //N倍插值interpolation <=comb[STAGES-1];cont<=0;endelseinterpolation <=0;end
end

2.4 积分器模块(N*fs)

// 积分器逻辑（由输出时钟驱动）
always @(posedge clk_out or posedge reset) beginif (reset) beginfor (i = 0; i <STAGES; i = i + 1) beginintegrator[i] <= 0;endoutput_buffer <= 0;end else beginintegrator[0] <= interpolation;for (i = 1; i <STAGES; i = i + 1) begin //积分器integrator[i] <= integrator[i] + integrator[i-1];endoutput_buffer<=integrator[STAGES-1];end
end

一级integartor的RTL图
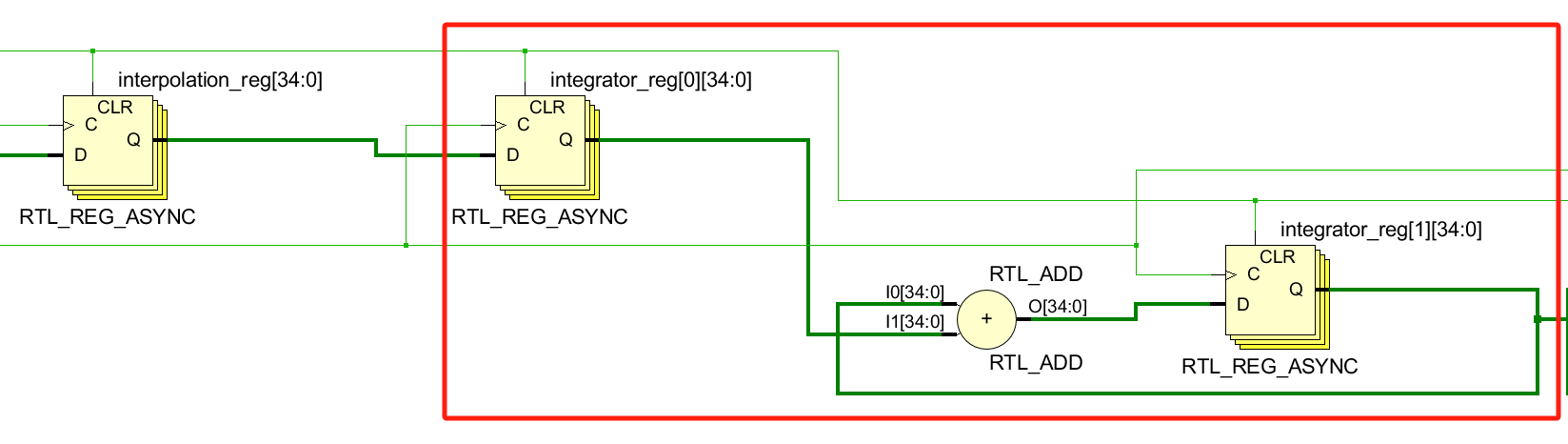
在这里插入图片描述

三、CIC插值滤波器实现

实验仅进行行为仿真验证

3.1 testbench

module testCIC();
reg clk,reset;
reg sclk;
wire [7:0]RA;
wire [15:0]RD;
wire [15:0]RO;initial beginclk  = 1'b0;sclk  = 1'b0;#100 reset=1'b1;#500 reset=1'b0;endalways begin#1 clk =~clk;
endalways begin#96 sclk =~sclk;
end//正弦信号输出
count count1(   .CLK(sclk),.RST(reset),.RA(RA));
DDS DDS1(.CLK(sclk),           .RA(RA),       .RDQ(RD));
//CIC插值滤波
CIC cic1(.clk_in(sclk),  .clk_out(clk), .reset(reset),  .data_in(RD), .data_out(RO) 
);
endmodule

3.2 仿真分析

上变频时钟周期为2ns，输入时钟为192ns，图中data_in和data_out周期比例为96，符合预期设计
在这里插入图片描述
CIC插值滤波后的波形未出现波形失真，但存在幅度减小的情况(这里暂未弄清楚是滤波增益造成还是输入数据的问题)

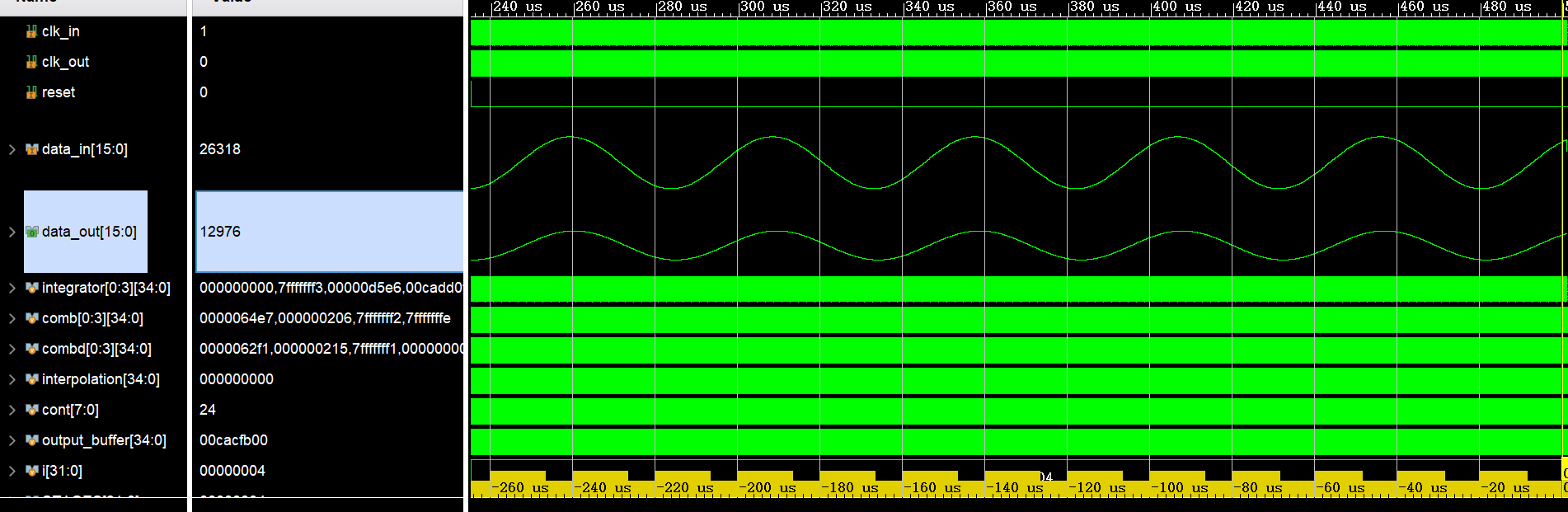
中间梳妆器和积分器的过程就不再展示，可自行进行实验观测。