逻辑代数点

本文主要是介绍逻辑代数点，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

与

条件同时具备，结果发生
Y=A AND B = A&B=A·B=AB

图像表示: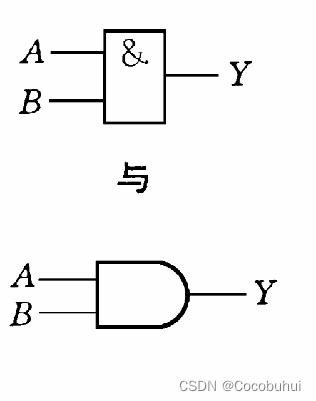
数字表示:

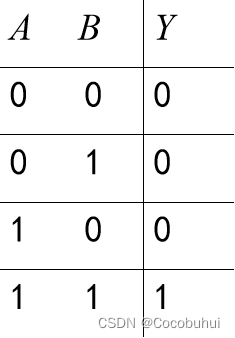
小结: 与出现0则0, 双一则一.

或

条件之一具备，结果发生
Y= A OR B = A+B
图像表示:

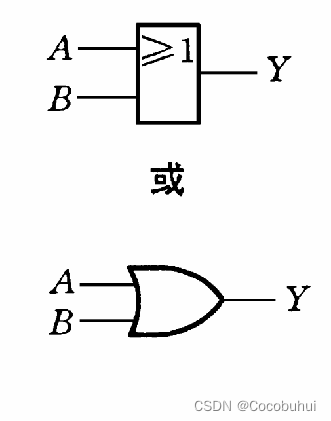
数字表示:

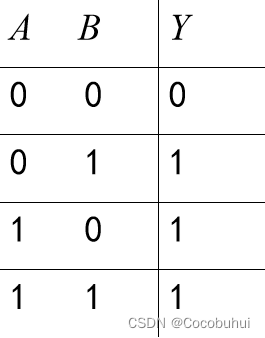
小结: 出1则1,双0则0, 跟(与)想反

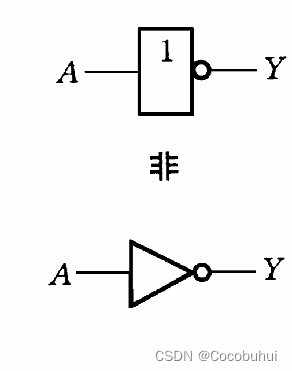
非

条件不具备，结果发生

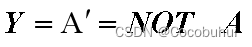
相当于不
图像表示:

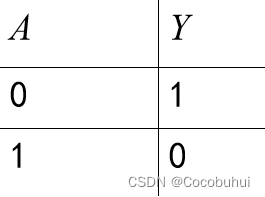
数字表示:

与非 或非 与或非

• 与非
  -
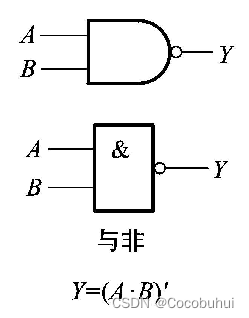
  与应该是 用 * 表示
  非 应该是 用 ’ 表示

• 或非
  
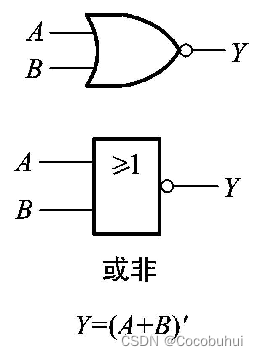
  或 应该是用 + 表示

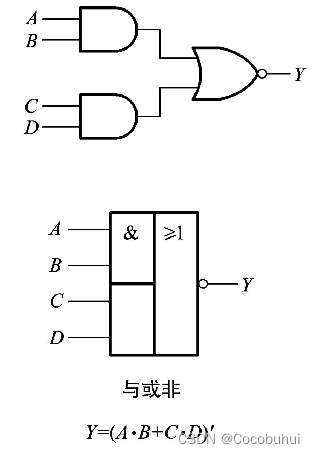
• 与或非

异或

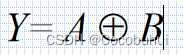
图像表示:

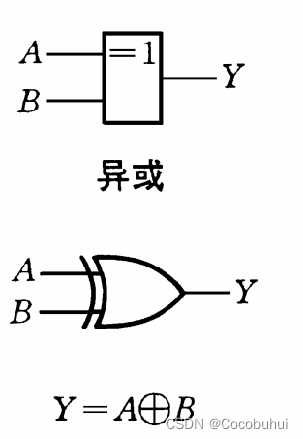
数字表示:

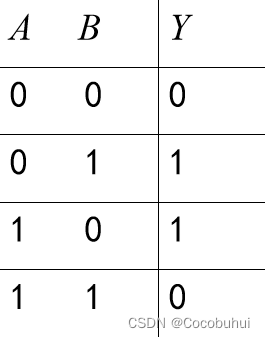
小结:相当于有1则1,双0或双一则相反.

同或

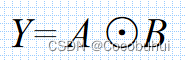
图像表示:

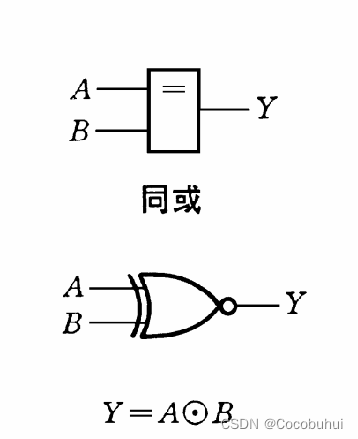
数字表示:

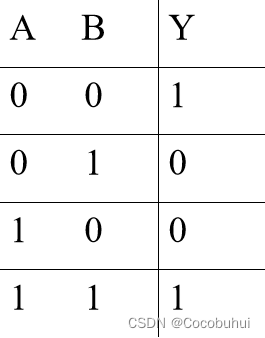
小结: 相当于有0则0,双0或双1 为 1

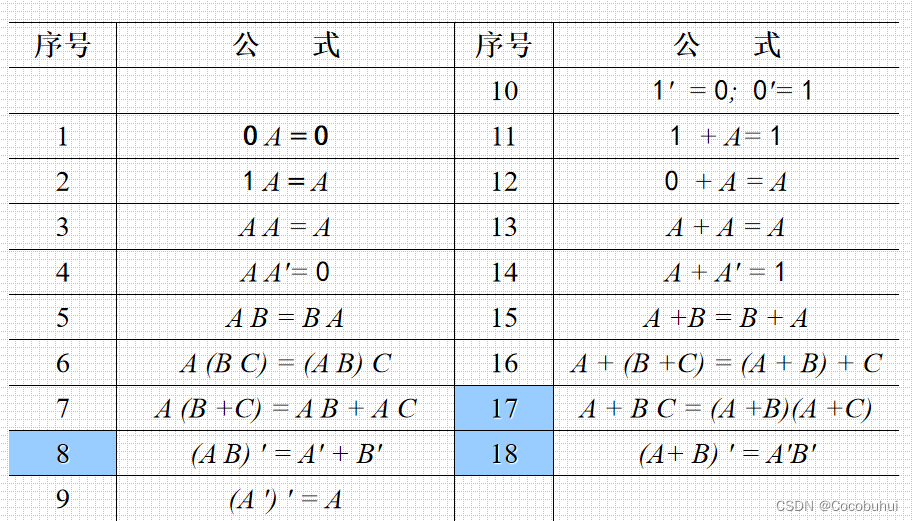
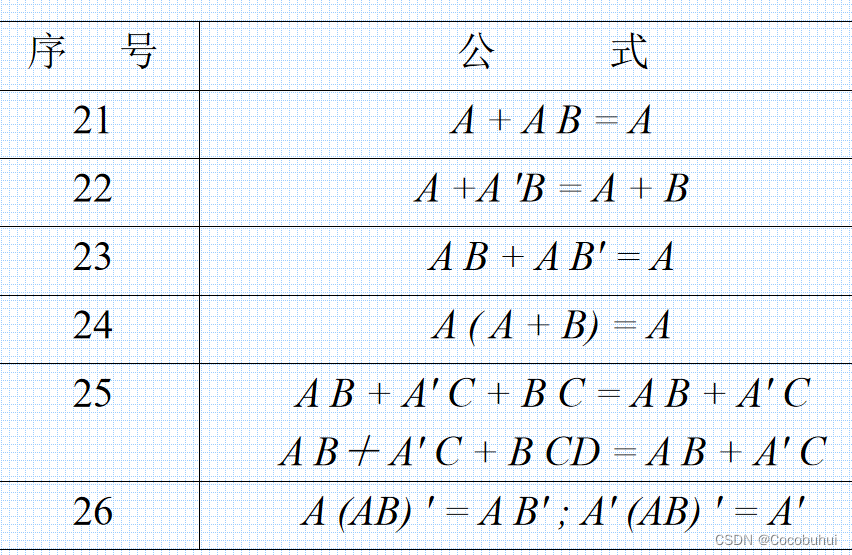
布尔恒等式

代入定理

例子

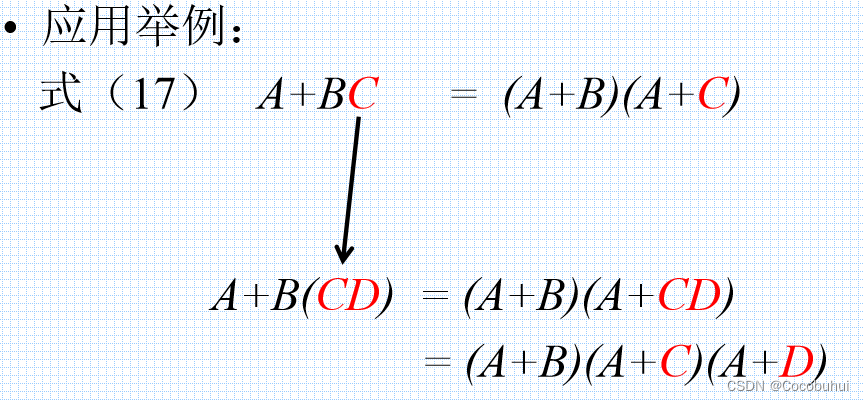
例子

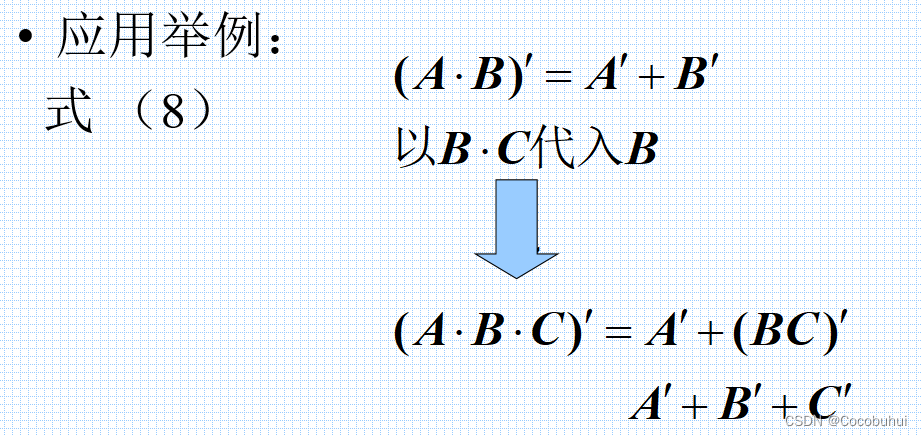
反演定理

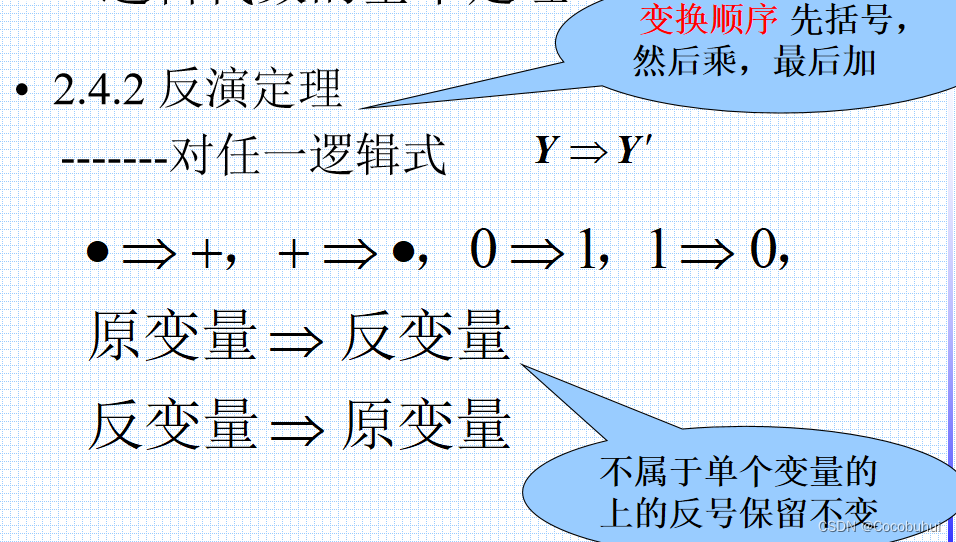
规则: “.“换”+”,“+“换”.”
“0"换"1”，"1"换"0
原变量换反变量，反变量换原变量

例子

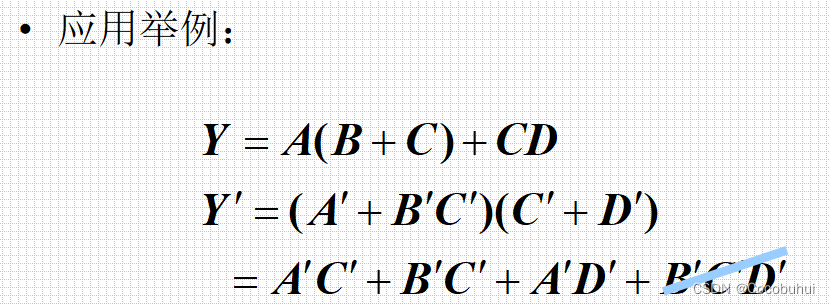
B’C’D’=B’C’(1+D’)
1+任何东西都为1
所以

例子:

若已知Y=A’B’+C’DE’+0
①".“换”+“,”+“换”.“得到Y=(A’+B’).(C’+D+E’).0
②"0"换"1”，"1"换"0"得到Y=(A’+B’).(C’+D+E’).1
③原变量换反变量，反变量换原变量得到Y’=(A+B).(C+D’+E).1

例子:

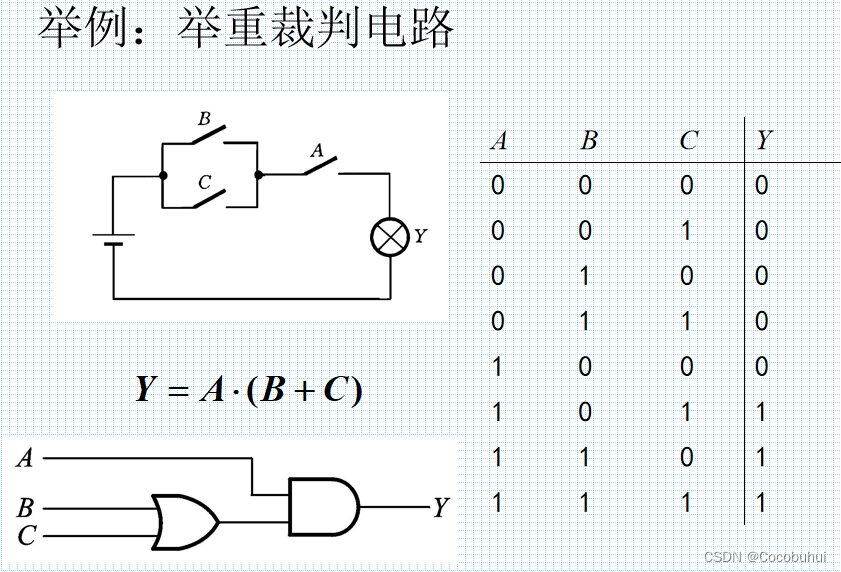
真值表 与 逻辑式：

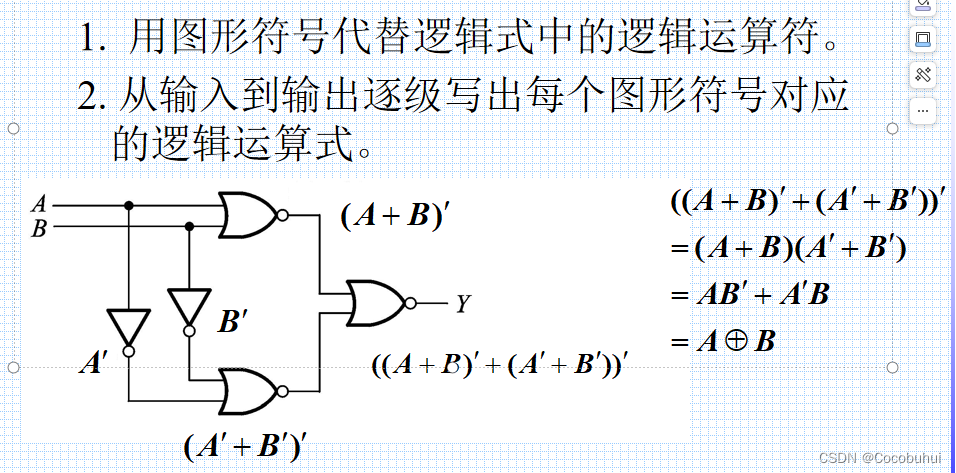
逻辑式 与 逻辑图

最小项

对于n变量函数,有2n个最小项

例子:

最小项编号

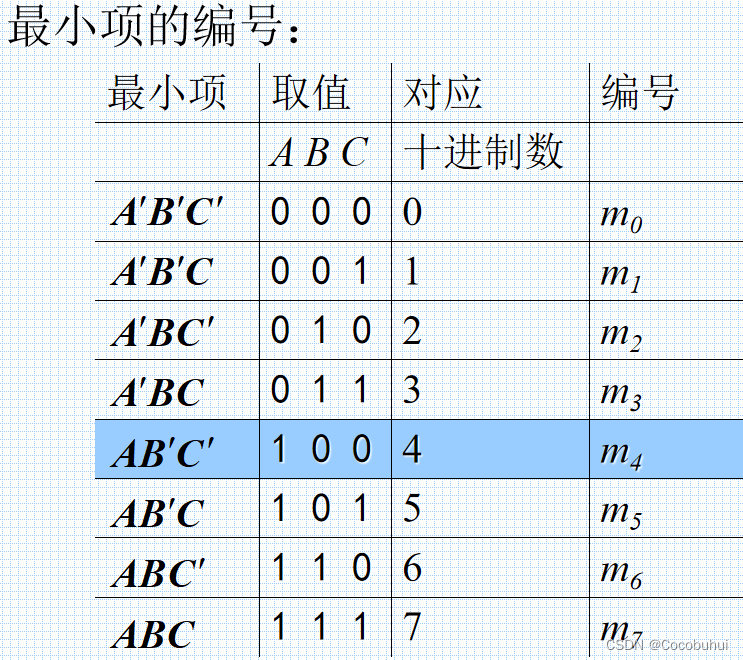
这里相当于8进制

最小项性质

在输入变量任一取值下，有且仅有一个最小项的值为1。
全体最小项之和为1 。
任何两个最小项之积为0 。
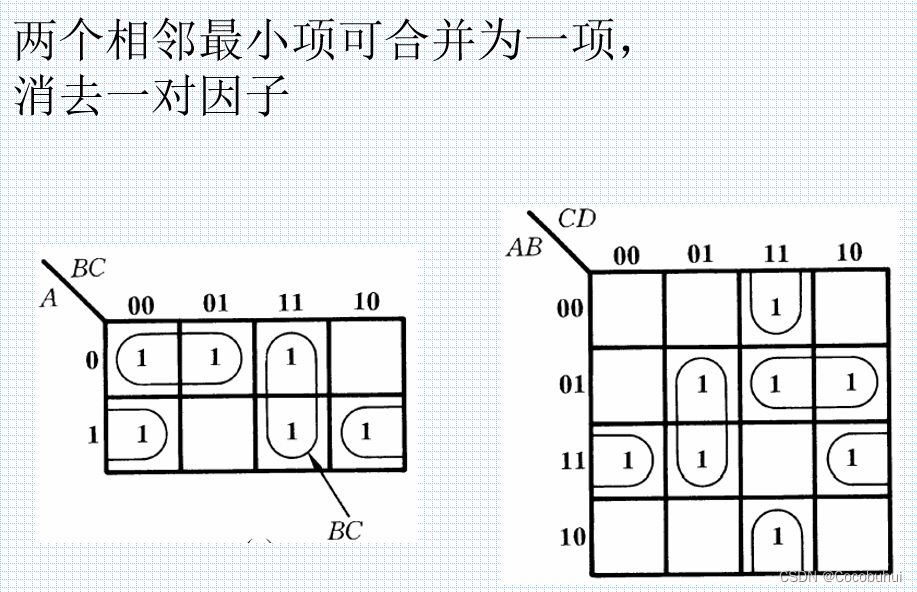
两个相邻的最小项之和可以合并，消去一对因子，只留下公共因子。
------相邻：仅一个变量不同的最小项

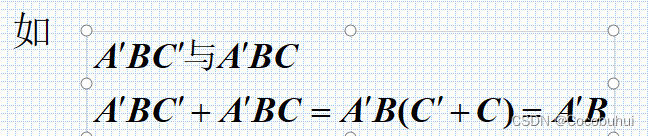
最小项之和

例子

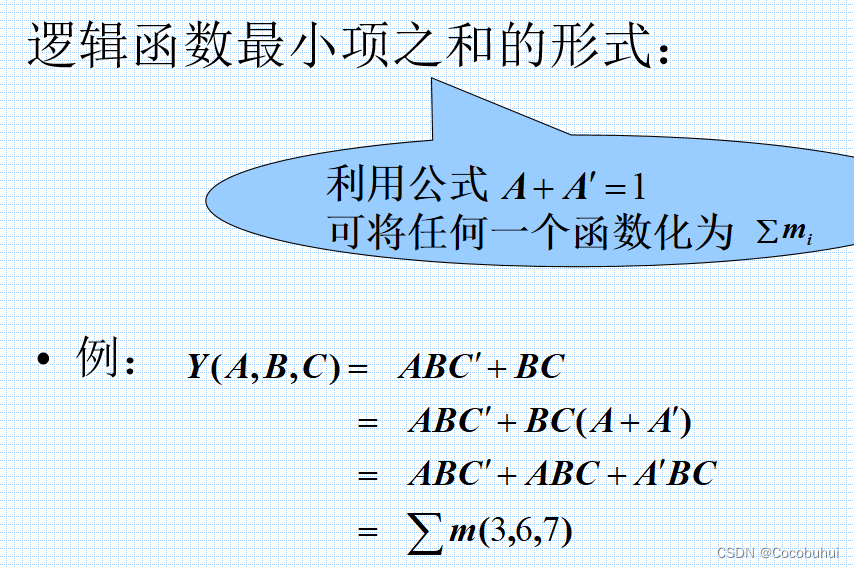
例子

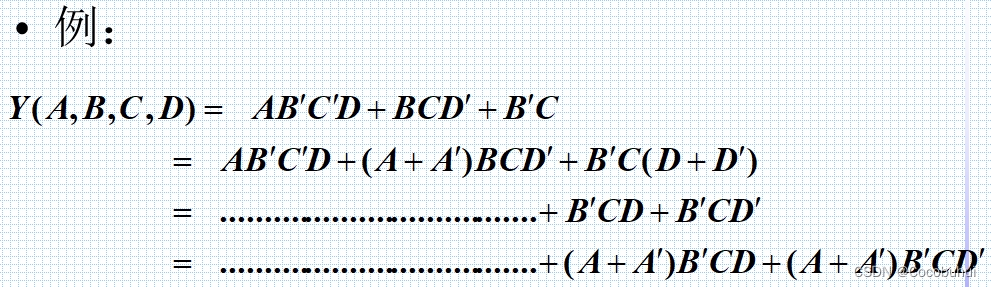
最大项

最大项性质

• 在输入变量任一取值下，有且仅有一个最大项的值为0；
• 全体最大项之积为0；
• 任何两个最大项之和为1；
• 只有一个变量不同的最大项的乘积等于各相同变量之和。

最大项编号

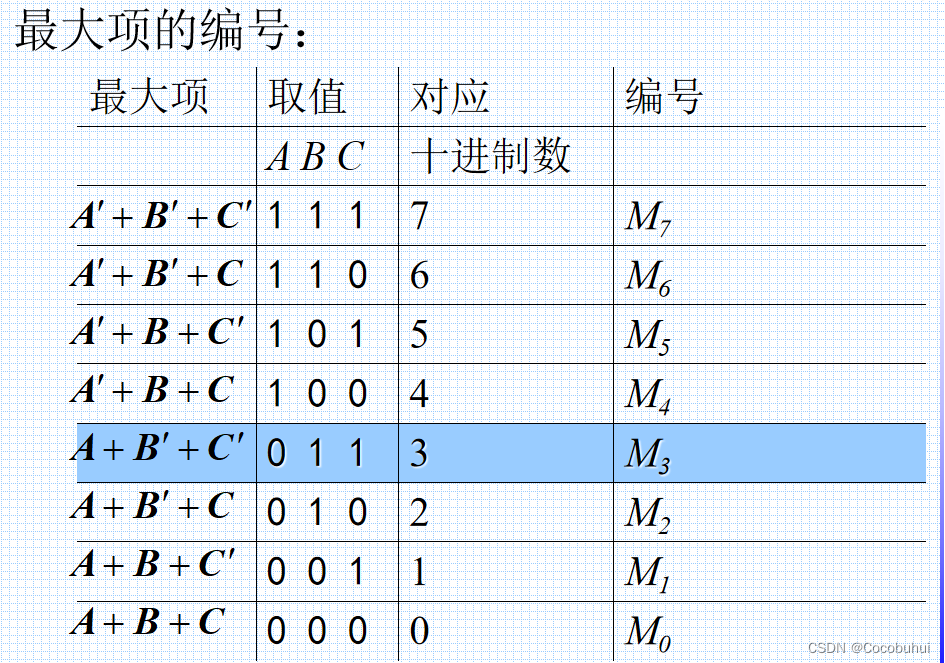
这里与最小项编号相反

逻辑代数的化简

公式化简法

• 反复应用基本公式和常用公式，消去多余的乘积项和多余的因子。
  

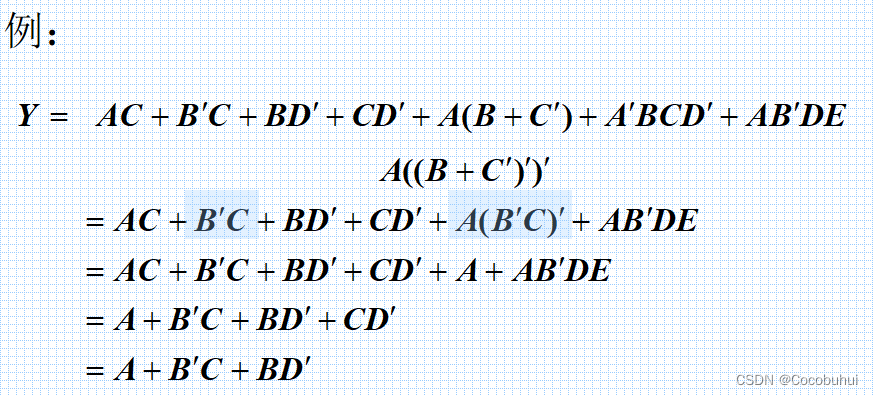
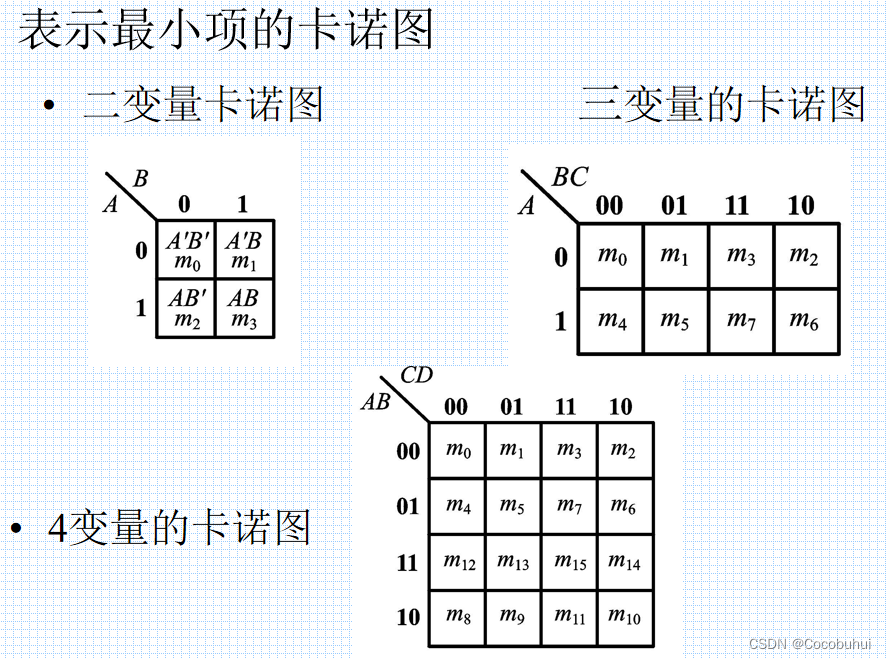
卡诺图化简法

• 实质：将逻辑函数的最小项之和的以图形的方式表示出来

• 以2n个小方块分别代表 n 变量的所有最小项，并将它们排列成矩阵，而且使几何位置相邻的两个最小项在逻辑上也是相邻的（只有一个变量不同），就得到表示n变量全部最小项的卡诺图。

表示逻辑代数

• 将函数表示为最小项之和的形式 。

• 在卡诺图上与这些最小项对应的位置上添入1，其余地方添0。

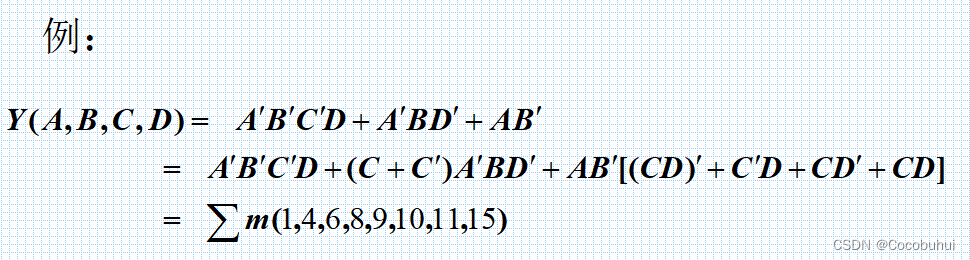
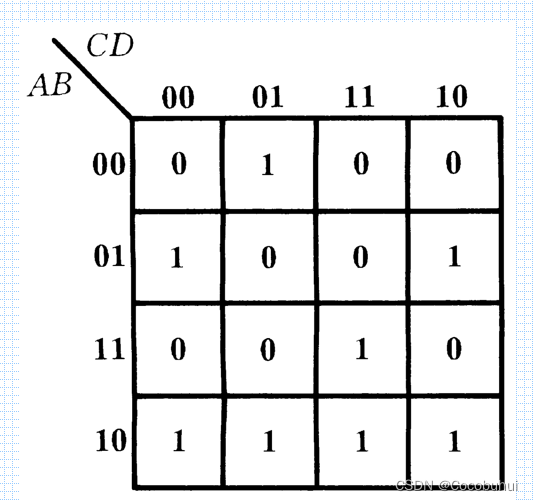
用卡诺图化简函数

• 依据：具有相邻性的最小项可合并，消去不同因子。

• 在卡诺图中，最小项的相邻性可以从图形中直观地反映出来。

• 合并最小项的原则：

1. 两个相邻最小项可合并为一项，消去一对因子
2. 四个排成矩形的相邻最小项可合并为一项，消去两对因子
3. 八个相邻最小项可合并为一项，消去三对因子
   
   **

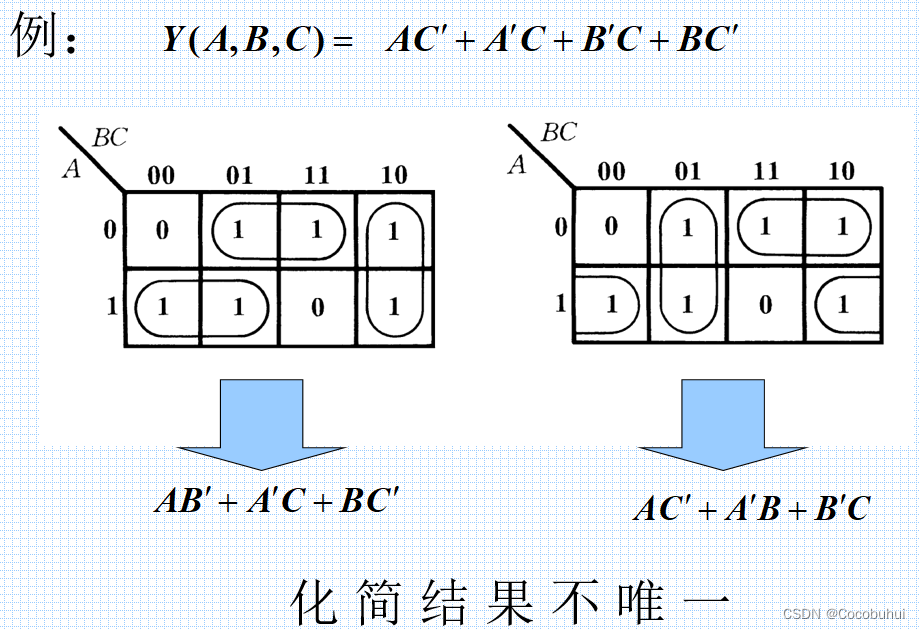
化简步骤：------用卡诺图表示逻辑函数------找出可合并的最小项------化简后的乘积项相加（项数最少，每项因子最少）

**

卡诺图化简的原则:
化简后的乘积项应包含函数式的所有最小项，即覆盖图中所有的1。乘积项的数目最少，即圈成的矩形最少。每个乘积项因子最少，即圈成的矩形最大.

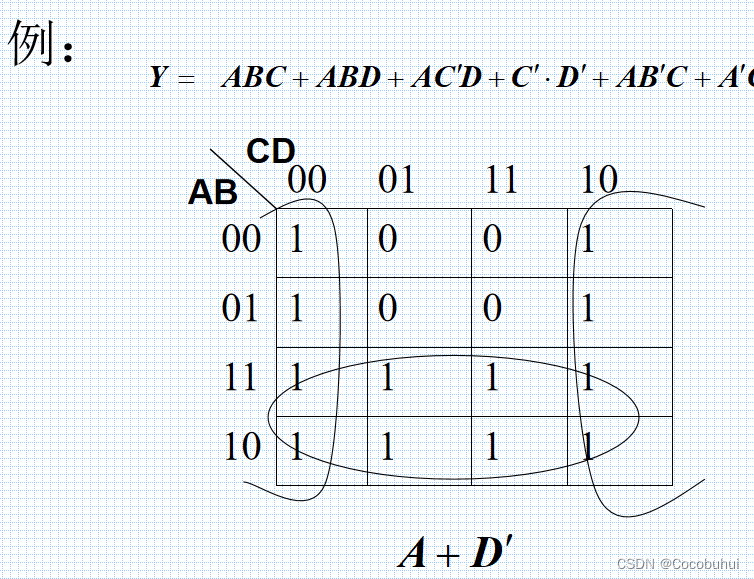
约束项

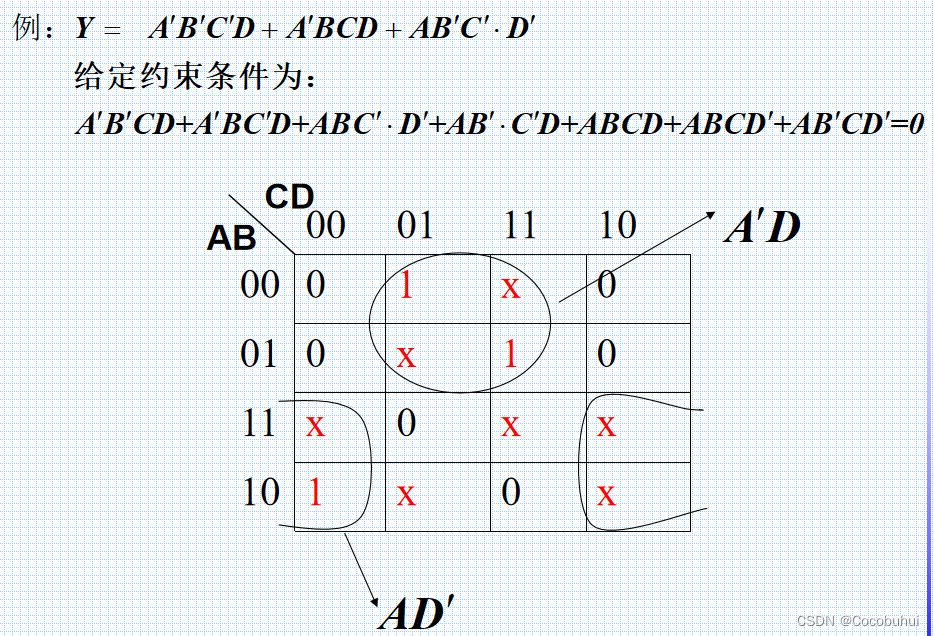
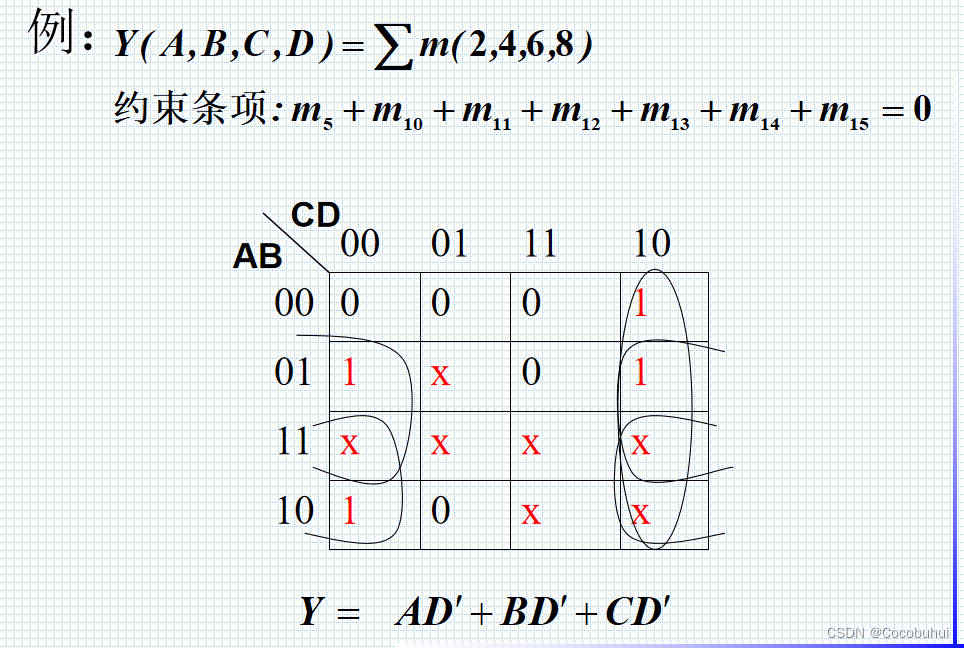
本文仅供作者本人复习使用,不正之处多多包涵

这篇关于逻辑代数点的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---