本文主要是介绍马上蓝桥了,干货总结基础树论知识点,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
今日知识点:
对于每个子树如果和小于0就返回0;如果大于0就直接返回。
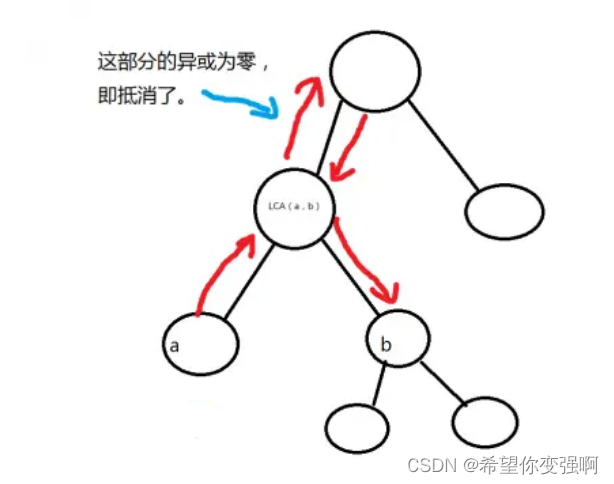
注意异或的性质,偶消奇不消,所以lca上面的都消掉了,并不需要跑lca,也就是说只需要把根到所有点的距离跑出来即可
如果上传过来小于k个,我们是考虑把当前根节点也加入其中;如果大于k,那就直接返回失败;等于k忽略
这棵树的深度就是这棵树上到根节点的最长距离+1;这棵树的宽度就是到根节点距离相同的节点个数的最大值。
最大子树和
思路:
树上异或
思路:
树的分解
思路:
二叉树问题
思路:
最大子树和

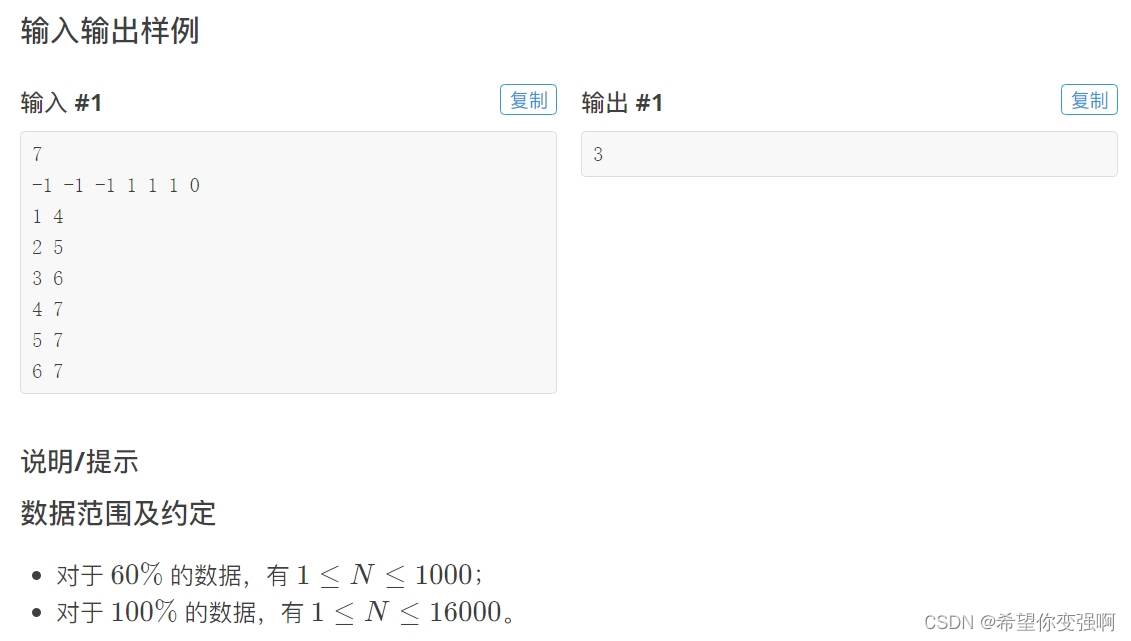
思路:
对于每个子树:如果子树和小于0,直接丢掉吧,所以返回0;如果大于0就直接返回。
#include <bits/stdc++.h>
using namespace std;
const int N=2e4;
typedef long long ll;
vector<int>ve[N];
ll ans,n,a[N],f[N],INF=-1e11;
int dfs(int u,int fa){for(int i=0,sz=ve[u].size();i<sz;i++){int v=ve[u][i];if(v==fa)continue;f[u]+=dfs(v,u);}f[u]+=a[u];ans=max(f[u],ans);if(f[u]<0)return 0;else return f[u];
}
int main(){cin>>n;int x,y;ans=INF;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n-1;i++){cin>>x>>y;ve[x].push_back(y);ve[y].push_back(x);}dfs(1,-1);cout<<ans;
}
树上异或


思路:
注意异或的性质,偶消奇不消,所以lca上面的都消掉了,并不需要跑lca(你喜欢写LCA代码吗?)也就是说只需要把根到所有点的距离跑出来即可
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int tot,n,m,head[N],f[N];
struct node{int to,w,next;}e[N*2];
void add(int u,int v,int w){e[++tot]={v,w,head[u]};head[u]=tot;}
void dfs(int u,int fa,int num){f[u]=num;for(int i=head[u];i;i=e[i].next){int v=e[i].to,w=e[i].w;if(fa==v)continue;dfs(v,u,num^w);}
}
int main(){cin>>n;int u,v,w;for(int i=1;i<n;i++){scanf("%d%d%d",&u,&v,&w);add(u,v,w);add(v,u,w); }dfs(1,0,0);cin>>m;for(int i=1;i<=m;i++){scanf("%d%d",&u,&v);printf("%d\n",f[u]^f[v]); }return 0;
}
树的分解
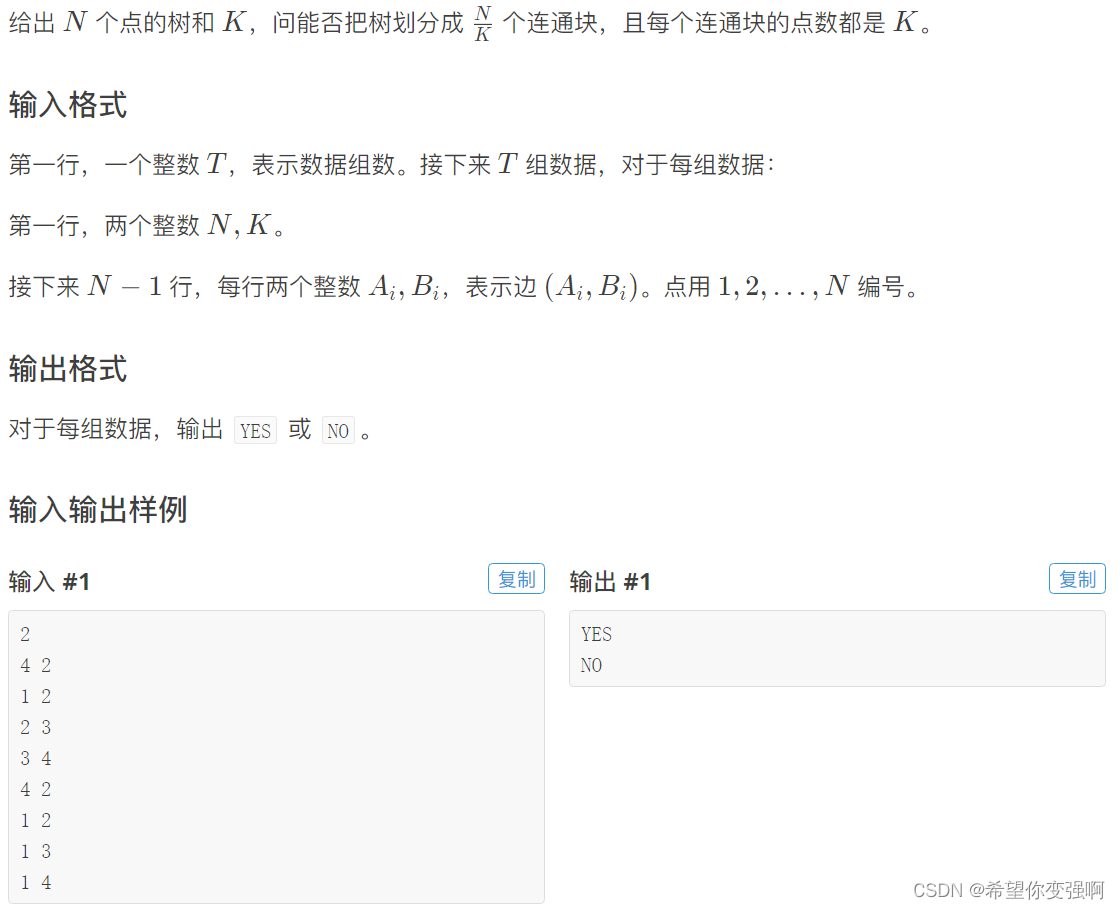

思路:
此题不好做,首先要明白最终的效果,必然是k个联通的,那么对于每个节点来说,如果孩子匹配不成功,是可以和父亲继续匹配的,也就是上传当前个数即可。
那么对于节点来说:一定是和上传过来的未匹配成功的孩子都保持一个颜色,
否则就联通不了,你可以画图证明。(因为如果匹配成功就可以忽略)
那么如果上传过来小于k个,我们是考虑把当前根节点也加入其中;如果大于k,那就直接返回失败;等于k忽略
#include <bits/stdc++.h>
using namespace std;
int n,k,t,sum;
vector<int>ve[100005];
int dfs(int u,int fa){int ans=1;//初始化上传数for(int i=0,sz=ve[u].size();i<sz;i++){if(ve[u][i]==fa)continue;int a=dfs(ve[u][i],u);if(a==-1||a>k)return -1;//这段还认识吗,高速公路哦else if(a==k)continue;//直接上传0ans+=a;//更新上传数}return ans;
}
int main(){cin>>t;while(t--){cin>>n>>k;int a,b;for(int i=0;i<=n;i++)ve[i].clear();for(int i=1;i<n;i++){cin>>a>>b;ve[a].push_back(b);ve[b].push_back(a);}int ans=dfs(1,1);if(ans==k)cout<<"YES\n";//包括根节点在内仅上传k个则代表成功分解else cout<<"NO\n";}return 0;
}
二叉树问题

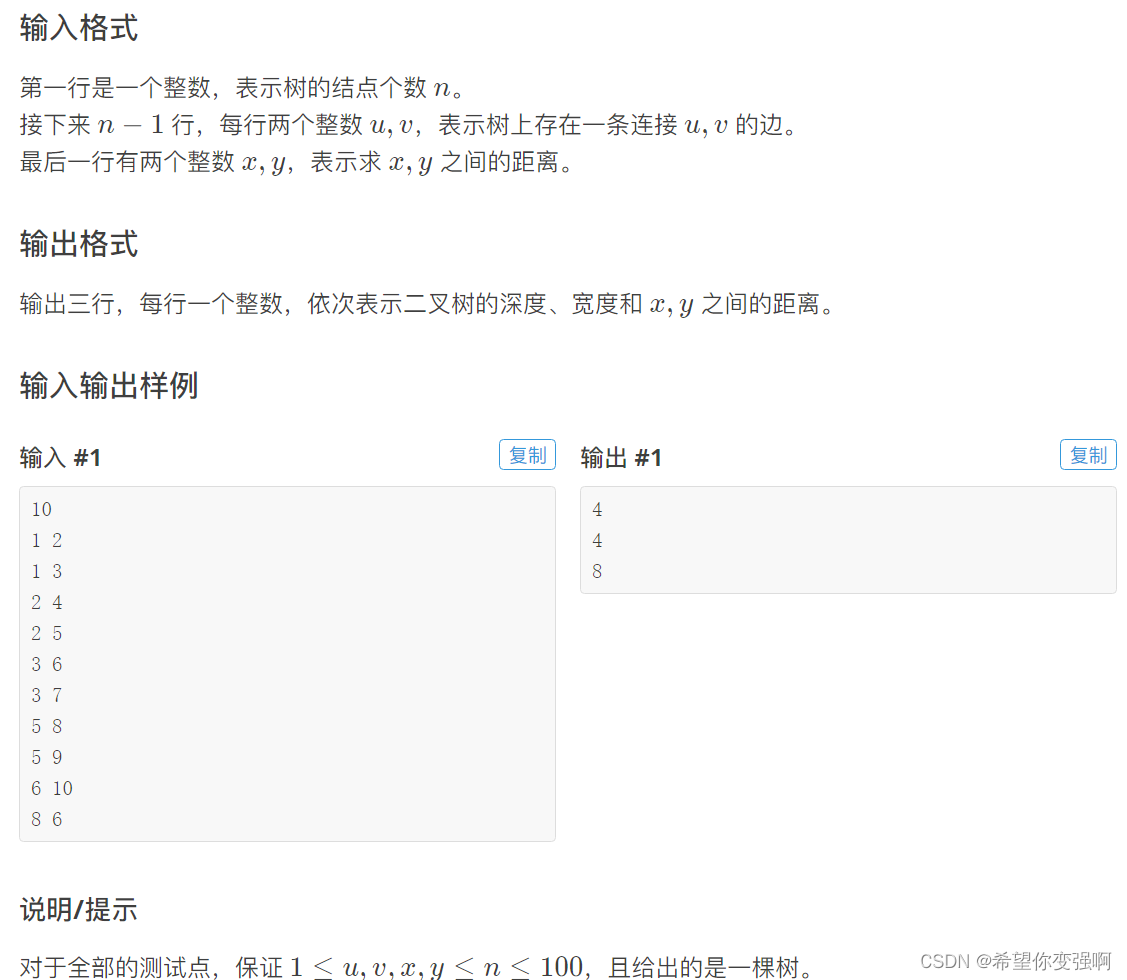
思路:
树的深度好说,宽度很容易让人想到树的直径(【算法每日一练]-图论(保姆级教程篇16 树的重心 树的直径)#树的直径 #会议 #医院设置-CSDN博客)感兴趣可以看看啊!
但是!!!这俩玩意不是一个东西哈,直径是直径,宽度是宽度。
现在要求查询这棵树的深度,其实就是这棵树上到根节点的最长距离+1;查询这棵树的宽度,其实就是到根节点距离相同的节点个数的最大值。
要处理第3个问题,一个很巧妙的做法是直接就把指向叶子方向的边权设为1,指向根方向的边权设为2。然后最短路即可
#include <bits/stdc++.h>
using namespace std;//拿图
const int N=200;
int n,ans,tot,dis[N],vis[N],head[N],tmp[2000];
struct node{int to,w,next;}e[N*2];
void add(int u,int v,int w){e[++tot]={v,w,head[u]};head[u]=tot;}
void spfa(int s){queue<int>q;q.push(s);memset(dis,0x3f,sizeof(dis));memset(vis,0,sizeof(vis));vis[s]=1;dis[s]=0;while(!q.empty()){int u=q.front();q.pop();vis[u]=0;for(int i=head[u];i;i=e[i].next){int v=e[i].to,w=e[i].w;if(dis[v]>dis[u]+w){dis[v]=dis[u]+w;if(!vis[v]){vis[v]=1;q.push(v);}}}}
}
int main(){cin>>n;int u,v;for(int i=1;i<n;i++){//树是n点n-1边cin>>u>>v;add(u,v,1);add(v,u,2);}cin>>u>>v;spfa(1);for(int i=1;i<=n;i++)tmp[dis[i]]++,ans=max(ans,dis[i]);cout<<ans+1<<'\n';ans=0;for(int i=1;i<=2000;i++)ans=max(ans,tmp[i]);cout<<ans<<'\n';spfa(u);cout<<dis[v]<<'\n';
}这篇关于马上蓝桥了,干货总结基础树论知识点的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




