逻辑斯蒂回归中损失函数和代价函数的推导

本文主要是介绍逻辑斯蒂回归中损失函数和代价函数的推导，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

参见 Stanford CS230学习笔记（二）：Lecture 2 Basics, Logistic Regression and Vectorizing

逻辑斯蒂回归

公式

$\hat{Y}=\sigma (w^{T}X+b)$

其公式中的各项数据含义如下：

• 输入X：假设输入为一张64*64的图片，那么依次取出R、G、B矩阵中的所有像素值，我们可以得到一个64*64*3的向量，将其记作x，即为一个输入；将样本集中每个样本的x(i)按列排成(64*64*3)*m的矩阵，记作X
• 输出Yhat：Yhat是一个1*m的矩阵，每个值代表相应的x的输出，其中的hat代表预测值
• 参数w b：需要利用梯度下降等方法寻找的参数，以使后续的代价函数最小化
• σ：sigmoid函数，用以归一化，将括号中的值限定在(0,1)范围内，$\sigma (z)=\frac{1}{1+e^{-z}}$

损失函数与代价函数

在逻辑斯蒂回归中，损失函数(Lost function)为
$$L(\hat{y},y)=-(y\log (\hat{y})+(1-y)\log (1-\hat{y}))$$

代价函数(Cost function)为
$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})$$

推导

损失函数

逻辑斯蒂回归概率的基本公式为(csdn的latex不支持align…)

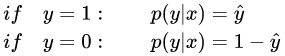
合并起来

$$p(y|x)={\hat{y}}^y\cdot (1-\hat{y}{)}^{(1-\hat{y})}$$

取对数，以保证函数单增

$$\log p(y|x)=y\log \hat{y}+(1-\hat{y})\log (1-\hat{y})$$
为了最大化概率（的对数），我们需要最小化损失函数，因此两者增减性相反，添加负号即可
$$L(\hat{y},y)=-(y\log (\hat{y})+(1-y)\log (1-\hat{y}))$$

代价函数

代价函数的公式是根据极大似然估计来的，就是数理统计里面那一套，样本先相乘再求对数，对数求导使导数等于0，得到极大似然估计值

至于为什么最后相乘变成了相加，是因为对数的存在，将连乘的对数变成了各项对数的连加

对于m个样本的整个训练集，服从独立同分布的样本的联合概率就是每个样本的概率的乘积

$$\log \prod _{i=1}^{m}p(y^{(i)}|x^{(i)})=\sum _{i=1}^m\log p(y^{(i)}|x^{(i)})=-\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})$$

极大化似然概率就是极小化代价函数，因此增减性相反加负号，此处还要除上m

$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})$$

这篇关于逻辑斯蒂回归中损失函数和代价函数的推导的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---