本文主要是介绍马上蓝桥杯了,干货总结动态规划专题,祝你考场爆杀(拔高篇)最佳课题选择 书本整理 打鼹鼠 吃吃吃 非零字段划分,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
最佳课题选择
思路:
书本整理
思路:
打鼹鼠
思路:
吃吃吃
思路:
非零字段划分
最佳课题选择

思路:
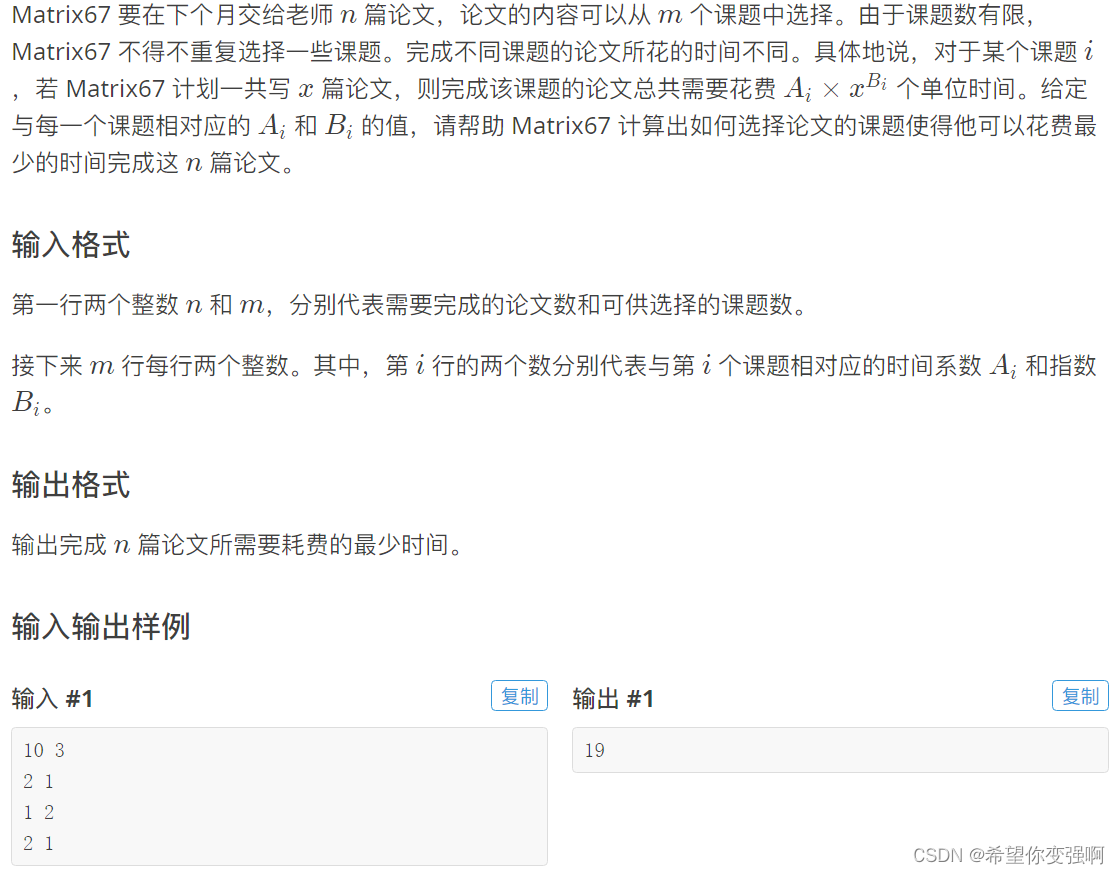
根本还是论文的分配,每个课题分配多少个论文是不确定的,这个也是很影响转移的。
也就是说当前已经遍历到第i个课题,那么从i-1课题转移过来的论文数应该依次遍历取最优。
那么设置f[i][j]已经遍历到第i个课题,且已经分配了j个论文对应的总花费时间。
f[i][j]=min(f[i-1][j-k]+f(k)) k<j f(k)表示i-1个课题在k个论文下对应的花费
要额外注意初始化问题:
对于第一个课题对应所有论文情况都要初始化才行
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=205;
ll n,m,inf=1e18,a[N],b[N],f[N][N];
int main(){cin>>n>>m;for(int i=1;i<=m;i++)cin>>a[i]>>b[i];f[1][0]=0;for(int i=1;i<=n;i++)f[1][i]=a[1]*(ll)pow(i,b[1]);//注意隐式转换for(int i=2;i<=m;i++)for(int j=0;j<=n;j++){long long tmp=inf;for(int k=0;k<=j;k++){tmp=min(tmp,f[i-1][j-k]+a[i]*(ll)pow(k,b[i]));}f[i][j]=tmp;//获取最小的结果}cout<<f[m][n];return 0;
}
书本整理

思路:
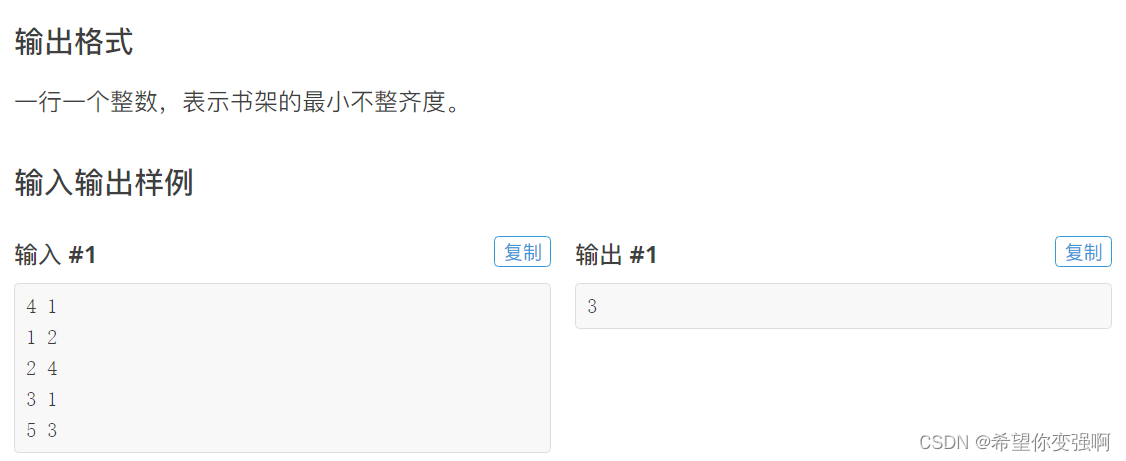
一定用好排序后的结果,我们注意到状态的转移和每次拿走的书关系不大,而是和其两旁的书关系很大,所以免不了我们需要关注每次拿走书的两旁的书,额?动态规划这么去想还写个屁呀!动态规划一定是从小状态到大状态的,不是从大状态到小状态的!!!
既然拿书不行我们就放书,注意到拿走书和那本书不放是等价的,而每本书都有放和不放
如果设置f[i][j]表示遍历到i本书(i书留下),当前总共留下了j本书对应的最小不整齐度。
你都知道了之前留下的书是哪一本了,后面的转移也就有了依据:
f[i][l]=min(f[j][l-1]+abs(a[i].y-a[j].y)) j<i l<min(i,m)
看不懂我解释一下:当前第i本留下,且一共留下l本书的情况可以从第i-1本留下且一共留下l-1本转移,也可以从第i-2,i-3……本留下且一共留下l-1本转移,那么我们只需要用到a[i]和a[j]即可。
#include <bits/stdc++.h>
using namespace std;
int f[300][300],n,k,ans=1e8;
struct node {int x,y;}a[300];
bool cmp(node c,node d){if(c.x!=d.x)return c.x<d.x;else return c.y<d.y;
}
int main(){cin>>n>>k;int m=n-k;for(int i=1;i<=n;i++){cin>>a[i].x >>a[i].y;}sort(a+1,a+1+n,cmp);memset(f,0x3f,sizeof(f));for(int i=1;i<=n;i++)f[i][1]=0;for(int i=2;i<=n;i++)//i是尝试放第i本书for(int j=1;j<i;j++){for(int l=2;l<=min(i,m);l++){//l是留下的本书f[i][l]=min(f[i][l],f[j][l-1]+abs(a[i].y-a[j].y));}}for(int i=m;i<=n;i++)ans=min(ans,f[i][m]);cout<<ans;
}
打鼹鼠

思路:
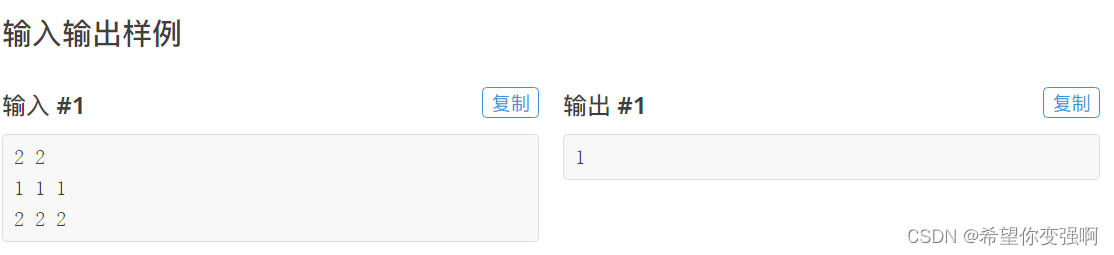
m个时间,每个时间都有一个鼹鼠出现,如果我们尝试去找起点跑图或者dp,肯定要开二维,但是还要记录当前的时间,因为你的步数不一定等于时间嘛,你可以停在原地的,所以就要开三维。
所以这是不可以的,然后注意到题上有个信息就是鼹鼠出现时间按照增序给你,那么不妨从鼹鼠下手。
因为每次转移都要清楚上一个鼹鼠的坐标,所以我们必须把当前打的最后一个鼹鼠坐标也好序号也罢给出,
所以就想到了设置f[i]表示到以第i只鼹鼠结尾的打的最多鼹鼠数,如果设置f[i]表示到第i时间打到的最多鼹鼠数还是做不了的。
f[i]=max(f[i],f[j]+1) 然后能不能转移只需要判断曼哈顿距离即可
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
struct node{int x,y,t;}a[N];
int n,m,f[N],ans;
int dis(int x,int y,int xx,int yy){return abs(x-xx)+abs(y-yy);
}
int main(){cin>>n>>m;for(int i=1;i<=m;i++)cin>>a[i].t>>a[i].x>>a[i].y;for(int i=1;i<=m;i++){f[i]=1;for(int j=1;j<i;j++)if(dis(a[i].x,a[i].y,a[j].x,a[j].y)<=a[i].t-a[j].t)f[i]=max(f[i],f[j]+1);ans=max(ans,f[i]); }cout<<ans;
}
吃吃吃

思路:
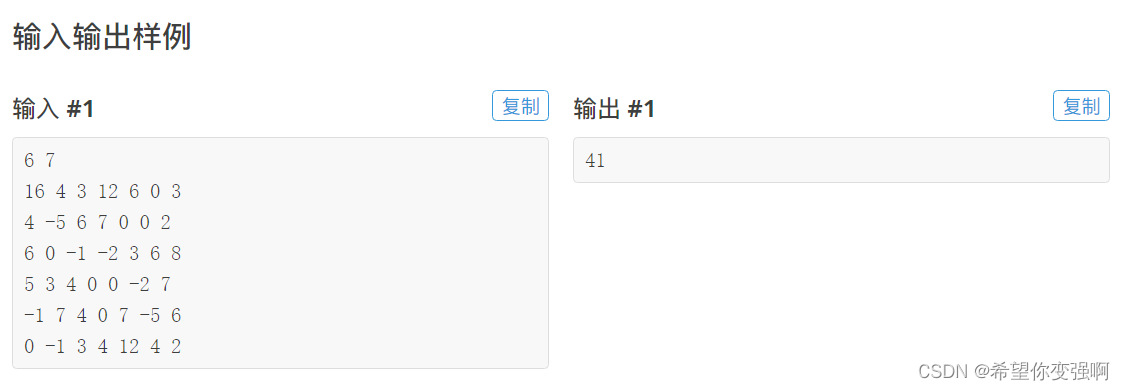
一开始我在想:从下往上走
那么我就自下而上的去dp,但是发现这样的话有些点的状态是错误的,然后就特别想去模拟这个dp。
最开始想的是bfs,但是这样的话每个点只能被更新一次,并不能达到正确更新,那么如果借鉴spfa的更新技巧或许可以解决这个问题,于是打出了这篇题解。
#include <bits/stdc++.h>
using namespace std;
int ans,a[300][300],f[300][300];
bool vis[300*300];
struct node{int x,y;};
queue<node>q;
int main(){int m,n;cin>>m>>n;for(int i=1;i<=m;i++)for(int j=1;j<=n;j++)cin>>a[i][j];q.push(node{m+1,n/2+1});//一定要注意起点memset(f,-0x3f,sizeof(f));f[m+1][n/2+1]=0;vis[(m+1)*n+n/2+1]=1;//vis表示是否在队列中,有环我们只管走,有spfa别怕while(!q.empty()){node cur=q.front();q.pop();vis[cur.x*n+cur.y]=0;for(int i=-1;i<=1;i++){int tx=cur.x-1,ty=cur.y+i;if(tx<=0||tx>m||ty<=0||ty>n)continue;if(f[tx][ty]<f[cur.x][cur.y]+a[tx][ty]){f[tx][ty]=f[cur.x][cur.y]+a[tx][ty];if(!vis[tx*n+ty])q.push(node{tx,ty}),vis[tx*n+ty]=1;}}}for(int i=1;i<=m;i++)for(int j=1;j<=n;j++)ans=max(ans,f[i][j]);cout<<ans;
}
也是非常高兴啊,然后看了别人的题解,我tm真是想多了,还是可以直接循环dp的,只要你设置好f的意义就可以从上向下dp,然后答案对应的f也很好求出
设置f[i][j]表示以此为起点能获取的最大能量,然后正向dp就行了
f[i][j]=max(max(f[i-1][j],f[i-1][j-1]),f[i-1][j+1])+a[i][j];
哎呀,也是想到了数字金字塔那道题,确实是一类的(【算法每日一练]-动态规划(保姆级教程 篇14) #三倍经验 #散步 #异或和 #抽奖概率-CSDN博客)
#include<iostream>
#include<cstring> //头文件
using namespace std;
int n,m,a[201][201],f[201][201]={0},x,y;
int main()
{cin>>n>>m;y=m/2+1;x=n; //求出李大水牛最开始的位置memset(a,-9999,sizeof(a)); //设置边界,为了避免李大水牛吃到餐桌外面去。。for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j]; //输入}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){f[i][j]=max(max(f[i-1][j],f[i-1][j-1]),f[i-1][j+1])+a[i][j]; //动态方程}}cout<<max(max(f[x][y],f[x][y-1]),f[x][y+1])<<endl; //因为最大值只可能在李大水牛的前方、左前方、右前方,所以只要找这三个的最大就行了return 0;
}这里也是给各位提一个醒,也是给自己再说一遍:
1,bfs跑图时候一定要把终点也吃进去才能检测到终点
2,如果dp要走环的话,就一定要提前保存cur的dp信息,否则就在循环中被修改,即:
f[tx][ty]=f[cur.x][cur.y]+1,后式在循环中可能就会被当场更新
非零字段划分

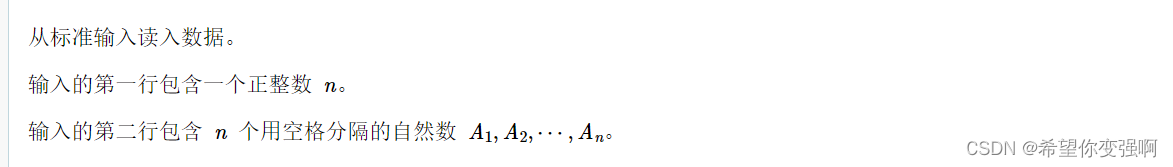

样例:11
3 1 2 0 0 2 0 4 5 0 2
差分法:
借助岛屿问题来分析此题。我们将一维数组具体成一排的岛屿。最开始p足够大,所有岛屿都被淹没cnt=0
海平面开始逐渐下降,那么慢慢的会有岛屿漏出水面,也会有岛屿合并为一个。
假设当前海平面为i时,高度恰为i的岛峰将会出现cnt++,高度恰为i的岛谷将会出现cnt--。我们不关心岛屿只关心岛峰和岛谷(因为只有这两种才影响答案)
所以我们的任务是预处理出所有的岛谷高度和岛峰高度。最后开始变化。
#include <bits/stdc++.h>
using namespace std;
const int N=5e5+5,M=1e4;
int a[N+2],d[M+1];
int main(){int n;cin>>n;for(int i=1;i<=n;i++)scanf("%d",&a[i]);a[0]=a[n+1]=0;n=unique(a,a+n+2)-a-1;//此时元素大小为n-1,去重便于统计峰和谷for(int i=1;i<n;i++){if(a[i-1]<a[i]&&a[i]>a[i+1])d[a[i]]++;else if(a[i-1]>a[i]&&a[i]<a[i+1])d[a[i]]--;}int ans=0,sum=0;for(int i=M;i>=1;i--)sum+=d[i],ans=max(ans,sum);cout<<ans;
}这篇关于马上蓝桥杯了,干货总结动态规划专题,祝你考场爆杀(拔高篇)最佳课题选择 书本整理 打鼹鼠 吃吃吃 非零字段划分的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





