聚类分析|基于层次的聚类方法及其Python实现

本文主要是介绍聚类分析|基于层次的聚类方法及其Python实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

0. 基于层次的聚类方法

层次聚类（Hierarchical Clustering）类似于一个树状结构，对数据集采用某种方法逐层地进行分解或者汇聚，直到分出的最后一层的所有类别数据满足要求为止。
当数据集不知道应该分为多少类时，使用层次聚类比较适合。
无论是凝聚方法还是分裂方法，一个核心问题是度量两个簇之间的距离，其中每个簇是一个数据样本集合。

划分方法（Partitioning Method）是基于距离判断样本相似度，通过不断迭代将含有多个样本的数据集划分成若干个簇，使每个样本都属于且只属于一个簇，同时聚类簇的总数小于样本总数目。如k-means和k-medoids。 该方法需要事先给定聚类数以及初始聚类中心，通过迭代的方式使得样本与各自所属类别的簇中心的距离平方和最小，聚类效果很大程度取决于初始簇中心的选择。

1. 簇间距离度量方法

1.1 最小距离

簇C1和C2的距离取决于两个簇中距离最近的数据样本。
$$dis{t}_{min}(C_1,C_2)=\underset{P_i\in C_1,P_j\in C_c}{\min }dist(P_i,P_j)$$

只要两个簇类的间隔不是很小，最小距离算法可以很好的分离非椭圆形状的样本分布，但该算法不能很好的分离簇类间含有噪声的数据集。

1.2 最大距离

簇C1和C2的距离取决于两个簇中距离最远的数据样本。
$$dis{t}_{max}(C_1,C_2)=\underset{P_i\in C_1,P_j\in C_c}{\max }dist(P_i,P_j)$$
最大距离算法可以很好的分离簇类间含有噪声的数据集，但该算法对球形数据的分离产生偏差。

1.3 平均距离

簇C1和C2的距离等于两个簇类中所有样本对的平均距离。
$$dis{t}_{average}(C_1,C_2)=\frac{1}{|C_1|.|C_2|}\sum _{P_i\in C_1,P_j\in C_c}dist(P_i,P_j)$$

1.4 中心法

簇C1和C2的距离等于两个簇中心点的距离。
$$dis{t}_{mean}(C_1,C_2)=dist(M_i,M_j)$$
其中M1和M2分别为簇C1和C2的中心点。

1.5 离差平方和

簇类C1和C2的距离等于两个簇类所有样本对距离平方和的平均。
$$dist(C_1,C_2)=\frac{1}{|C_1|.|C_2|}\sum _{P_i\in C_1,P_j\in C_c}(dist(P_i,P_j){)}^2$$

2. 基于层次的聚类算法

按照分解或者汇聚的原理不同，层次聚类可以分为两种方法：

2.1 凝聚（Agglomerative）

凝聚的方法，也称为自底向上的方法，初始时每个数据样本都被看成是单独的一个簇，然后通过相近的数据样本或簇形成越来越大的簇，直到所有的数据样本都在一个簇中，或者达到某个终止条件为止。
层次凝聚的代表是AGNES（Agglomerative Nesting）算法。

AGNES算法最初将每个数据样本作为一个簇，然后这些簇根据某些准则被一步步地合并。
这是一种单链接方法，其每个簇可以被簇中所有数据样本代表，两个簇间的相似度由这两个不同簇的距离确定（相似度可以定义为距离的倒数）。
算法描述：
输入：数据样本集D，终止条件为簇数目k
输出：达到终止条件规定的k个簇

1. 将每个数据样本当成一个初始簇；
2. 根据两个簇中距离最近的数据样本找到距离最近的两个簇；
3. 合并两个簇，生成新簇的集合；
4. 循环step2到step4直到达到定义簇的数目。

2.3 分裂（Divisive）

分裂的方法，也称为自顶向下的方法，它与凝聚层次聚类恰好相反，初始时将所有的数据样本置于一个簇中，然后逐渐细分为更小的簇，直到最终每个数据样本都在单独的一个簇中，或者达到某个终止条件为止。
层次分裂的代表是DIANA（Divisive Analysis）算法。
DIANA算法采用一种自顶向下的策略，首先将所有数据样本置于一个簇中，然后逐渐细分为越来越小的簇，直到每个数据样本自成一簇，或者达到了某个终结条件。
在DIANA方法处理过程中，所有样本初始数据都放在一个簇中。根据一些原则（如簇中最临近数据样本的最大欧式距离），将该簇分裂。簇的分裂过程反复进行，直到最终每个新的簇只包含一个数据样本。
算法描述：
输入：数据样本集D，终止条件为簇数目k
输出：达到终止条件规定的k个簇

1. 将所有数据样本整体当成一个初始簇；
2. 在所有簇中挑出具有最大直径的簇；
3. 找出所挑簇里与其它数据样本平均相异度最大的一个数据样本放入splinter group，剩余的放入old party中；
4. 在old party里找出到splinter group中数据样本的最近距离不大于到old party 中数据样本的最近距离的数据样本，并将该数据样本加入splinter group；
5. 循环step2到step4直到没有新的old party数据样本分配给splinter group；
6. splinter group和old party为被选中的簇分裂成的两个簇，与其他簇一起组成新的簇集合。

3. 基于层次聚类算法的Python实现

AgglomerativeClustering()是scikit-learn提供的层次聚类算法模型，常用形式为：

AgglomerativeClustering(n_clusters=2,affinity='euclidean',memory=None, compute_full_tree='auto', linkage='ward')

参数说明：

1. n_clusters：int，指定聚类簇的数量。
2. affinity：一个字符串或者可调用对象，用于计算距离。可以为：’euclidean’、’mantattan’、’cosine’、’precomputed’，如果linkage=’ward’，则affinity必须为’euclidean’。
3. memory：用于缓存输出的结果，默认为None（不缓存）。
4. compute_full_tree：通常当训练到n_clusters后，训练过程就会停止。但是如果compute_full_tree=True，则会继续训练从而生成一颗完整的树。
5. linkage：一个字符串，用于指定链接算法。若取值’ward’：单链接single-linkage，采用distmin；若取值’complete’：全链接complete-linkage算法，采用distmax；若取值’average’：均连接average-linkage算法，采用distaverage。

from sklearn import datasets
from sklearn.cluster import AgglomerativeClustering
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
import pandas as pd
iris = datasets.load_iris()
irisdata = iris.data
clustering = AgglomerativeClustering(linkage='ward', n_clusters= 4)
res = clustering.fit(irisdata)
print ("各个簇的样本数目：")
print (pd.Series(clustering.labels_).value_counts())
print ("聚类结果：")
print (confusion_matrix(iris.target, clustering.labels_))
plt.figure()
d0 = irisdata[clustering.labels_ == 0]
plt.plot(d0[:, 0], d0[:, 1], 'r.')
d1 = irisdata[clustering.labels_ == 1]
plt.plot(d1[:, 0], d1[:, 1], 'go')
d2 = irisdata[clustering.labels_ == 2]
plt.plot(d2[:, 0], d2[:, 1], 'b*')
d3 = irisdata[clustering.labels_ == 3]
plt.plot(d3[:, 0], d3[:, 1], 'c.')
plt.xlabel("Sepal.Length")
plt.ylabel("Sepal.Width")
plt.title("AGNES Clustering")
plt.show()

各个簇的样本数目：
1    50
2    38
0    36
3    26
dtype: int64
聚类结果：
[[ 0 50  0  0][ 1  0 24 25][35  0 14  1][ 0  0  0  0]]

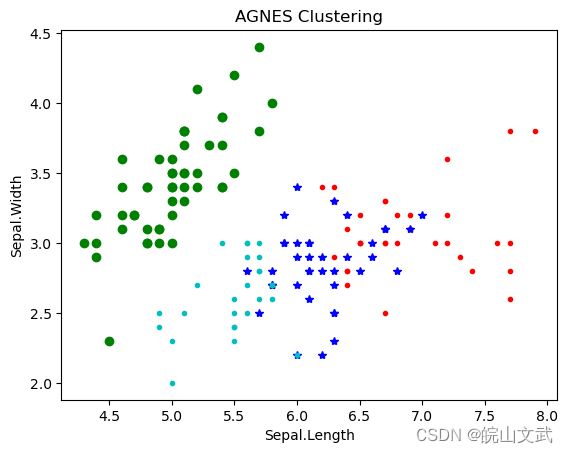
这篇关于聚类分析|基于层次的聚类方法及其Python实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---