本文主要是介绍【C++】哈希应用之位图,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
👀樊梓慕:个人主页
🎥个人专栏:《C语言》《数据结构》《蓝桥杯试题》《LeetCode刷题笔记》《实训项目》《C++》《Linux》《算法》
🌝每一个不曾起舞的日子,都是对生命的辜负
目录
前言
1.位图的概念
2.位图的模拟实现
2.1构造
2.2set
2.3reset
2.4test
3.源码
4.位图应用变形
前言
哈希是一种解决问题的思想,那么有关哈希的一个重要应用便是位图,该种结构适用于海量数据,数据无重复的场景,通常用来判断某个数据存在或者不存在,但只能处理整型数据。
欢迎大家📂收藏📂以便未来做题时可以快速找到思路,巧妙的方法可以事半功倍。
=========================================================================
GITEE相关代码:🌟樊飞 (fanfei_c) - Gitee.com🌟
=========================================================================
1.位图的概念
我们以一道面试题引入:
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中?
---『 腾讯』
根据题意,给定40亿个数,很明显如果是40亿个整型,1GB=10亿byte,40亿个整型=160亿byte=16GB,内存中根本放不下,那么这道题关键就在于只需要判断这个数是否在,所以我们仅需一个『 比特位』就可以表示某个数的状态,如果二进制比特位为1,代表存在,为0代表不存在。
而无符号整数总共有2^32个,因此我们仅需2^32个比特位=512M的内存空间就可以判断一个数是否在。
这种思想就是利用了哈希应用中的位图。
2.位图的模拟实现
很明显,位图的底层就是数组,那么我们就选用vector来当作底层容器。
2.1构造
在构造位图时,我们需要根据所给位数N,创建一个N位的位图,并且将该位图中的所有位都初始化为0。
一个整型有32个比特位,因此N个位的位图就需要用到N/32个整型,但是实际我们所需的整型个数是N/32+1,因为所给非类型模板参数N的值可能并不是32的整数倍。
例如,当N为40时,我们需要用到两个整型,即40/32+1=2。
//构造函数
bitset()
{_bits.resize(N / 32 + 1, 0);
}2.2set
set用于设置位,即设置某个数为存在,所处位设置为1。
设置位图中指定的位的方法如下:
- 计算出该位位于第 i 个整数的第 j 个比特位。
- 将1左移 j 位后与第 i 个整数进行或运算即可。
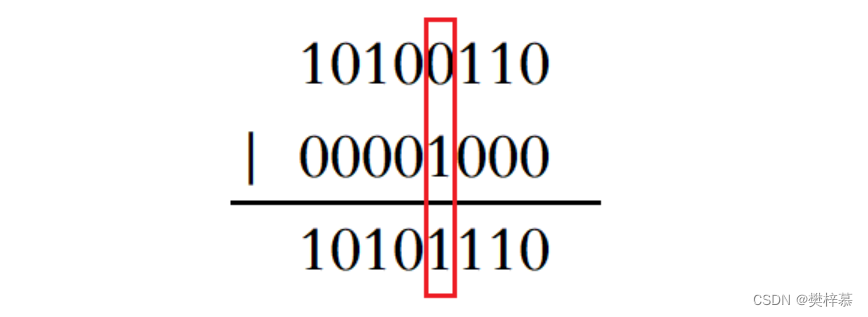
//设置位
void set(size_t pos)
{assert(pos < N);//算出pos映射的位在第i个整数的第j个位int i = pos / 32;int j = pos % 32;_bits[i] |= (1 << j); //将该位设置为1(不影响其他位)
}2.3reset
reset用于清空位,即设置某个数为不存在,所处位设置为0。
清空位图中指定的位的方法如下:
- 计算出该位位于第 i 个整数的第 j 个比特位。
- 将1左移 j 位再整体反转后与第 i 个整数进行与运算即可。
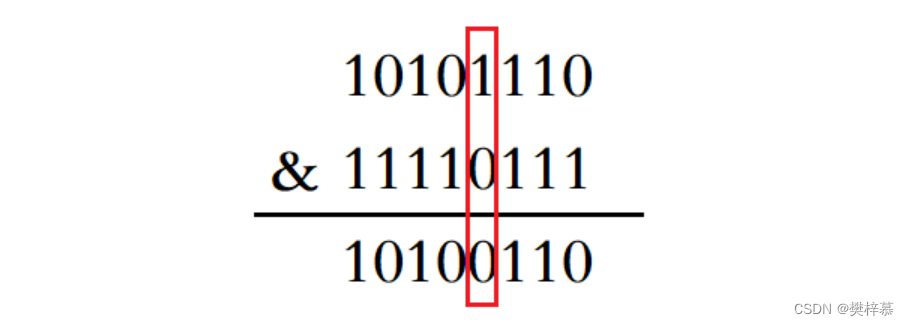
//清空位
void reset(size_t pos)
{assert(pos < N);//算出pos映射的位在第i个整数的第j个位int i = pos / 32;int j = pos % 32;_bits[i] &= (~(1 << j)); //将该位设置为0(不影响其他位)
}2.4test
test用于检验位,即判断某个数是否存在,检验所处位设置的值。
获取位图中指定的位的状态的方法如下:
- 计算出该位位于第 i 个整数的第 j 个比特位。
- 将1左移 j 位后与第 i 个整数进行与运算得出结果。
- 若结果非0,则该位被设置,否则该位未被设置。
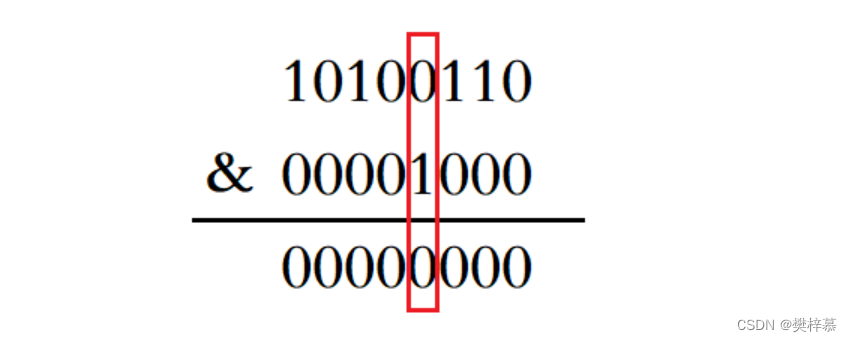
//获取位的状态
bool test(size_t x)
{assert(x <= N);//算出pos映射的位在第i个整数的第j个位size_t i = x / 32;size_t j = x % 32;return _bits[i] & (1 << j);
}3.源码
#pragma once
namespace bit_set
{template<size_t N>class bitset{public:bitset(){_bits.resize(N / 32 + 1, 0);}//设置位void set(size_t pos){assert(pos < N);//算出pos映射的位在第i个整数的第j个位int i = pos / 32;int j = pos % 32;_bits[i] |= (1 << j); //将该位设置为1(不影响其他位)}//清空位void reset(size_t pos){assert(pos < N);//算出pos映射的位在第i个整数的第j个位int i = pos / 32;int j = pos % 32;_bits[i] &= (~(1 << j)); //将该位设置为0(不影响其他位)} bool test(size_t x){assert(x <= N);size_t i = x / 32;size_t j = x % 32;return _bits[i] & (1 << j);}private:vector<int> _bits;};
}4.位图应用变形
问:1个文件有100亿个int,1G内存,设法找到出现次数不超过2次的所有整数。
这种问题很明显就是利用位图来解决,可是前面的问题我们只需要一个比特位就能标识出一个数字是否存在。
那么这个问题呢?
我们可以设想为3种状态,出现0次、出现1次、出现2次、出现3次及以上。
分别用如下数字标识:
出现0次:00
出现1次:01
出现2次:10
出现3次及以上:11
所以设计结构如下:
namespace two_bit_set
{template<size_t N>class two_bit_set{public:void set(size_t x){// 00 -> 01if (_bs1.test(x) == false&& _bs2.test(x) == false){_bs2.set(x);}else if (_bs1.test(x) == false&& _bs2.test(x) == true){// 01 -> 10_bs1.set(x);_bs2.reset(x);}}bool test(size_t x){if (_bs1.test(x) == false&& _bs2.test(x) == true){return true;}return false;}private:bitset<N> _bs1;bitset<N> _bs2;};
}给定两组数据找交集,我们也可以通过双位图这种思想实现。
=========================================================================
如果你对该系列文章有兴趣的话,欢迎持续关注博主动态,博主会持续输出优质内容
🍎博主很需要大家的支持,你的支持是我创作的不竭动力🍎
🌟~ 点赞收藏+关注 ~🌟
=========================================================================
这篇关于【C++】哈希应用之位图的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







