非线性跟踪-微分器 仿真应用

本文主要是介绍非线性跟踪-微分器 仿真应用，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

非线性跟踪微分器

实际工程问题中，测量信号经常不连续或者带随机噪声，需要提取连续信号和微分信号。比如PID调节中，需要由不连续的参考输入信号合理提取微分信号；编码器速度检测时，由数字的绝对位移信号提取出速度信号，或者速度信号提取加速度信号等等。当然可以采用线性微分器或者线性滤波等手段，然而“线性”办法可能还不能解决问题时，这里介绍“非线性”的方法，利用二阶最速开关系统构造出跟踪不连续输入信号并提取“近似微分”的“机构”。

非线性跟踪微分器的一般形式

$$\{\begin{array}{l}{z}_1^{{}^{\prime }}=z_2\\ z_1^{{}^{\prime }}=f(z_1,z_2)\end{array}(1)$$
的任意解都满足 z₁ ->0, z₂ ->0 (t->无穷）时，则对任意有界可积函数v(t) 和任意常数T > 0,系统
$$\{\begin{array}{l}{x}_1^{{}^{\prime }}=x_2\\ x_1^{{}^{\prime }}=R^{2}f(x_1-v,\frac{x_2}{R})\end{array}(2)$$
的解都满足
$$\underset{R\to \infty }{\lim }{\int }_0^T|x_1-v(t)|dt=0$$
详细见[1]

MATLAB仿真

离散微分跟踪器的MATLAB仿真

Matlab代码

function y=fst(x1,x2,u,r,h)
deta=r*h;			%h为步长  周期  r为调节系数，r越大跟踪效果越好，但微分信号会增加高频噪声
deta0=deta*h;	%反之，微分信号越平滑，会产生一定的滞后
y=x1-u+h*x2;
a0=sqrt(deta^2+8*r*abs(y));
if abs(y)<=deta0a=x2+y/h;
elsea=x2+0.5*(a0-deta)*sign(y);
endif abs(a)<=detay=-r*a/deta;
elsey=-r*sign(a);
end

% matlab 噪声信号仿真
clear
close allr=10;
h=0.01;                                 %执行步长
u_1 = 0;
x1(1)=0;
x2(1)=0;
ts = h;for k=1:1000time(k)=ts*k;dv(k) = cos(time(k));               %理想的微分信号u(k)=sin(time(k)) + 0.01*rands(1);  %加入噪声x1(k+1)=x1(k)+ts*x2(k);x2(k+1)=x2(k)+ts*fst(x1(k),x2(k),u(k),r,h);   du(k) = (u(k) - u_1)/ts;            %一般的差分计算u_1 = u(k);
end
x1(end)=[];
x2(end)=[];figure();
plot(time,x1,'r--',time,sin(time),'k-.','linewidth',2);
grid on
xlabel('Time(sec)','FontName','Times New Roman','FontSize',12,'FontWeight','bold')
h = legend('$x_1$','$sin$ ');
set(h,'Interpreter','latex','fontsize',14,'FontName','Times New Roman','fontweight','bold')
set(gca,'FontWeight','bold','fontsize',14,'FontName','Times New Roman')figure();
plot(time,x2,'r-',time,du,'b.',time,dv,'k-','linewidth',2);
grid on
xlabel('Time(sec)','FontName','Times New Roman','FontSize',12,'FontWeight','bold')
h = legend('$x_2$','diff','cos');                   %微分跟踪，差分跟踪，理想信号
set(h,'Interpreter','latex','fontsize',14,'FontName','Times New Roman','fontweight','bold')
set(gca,'FontWeight','bold','fontsize',14,'FontName','Times New Roman')

仿真 r = 50 T=0.01

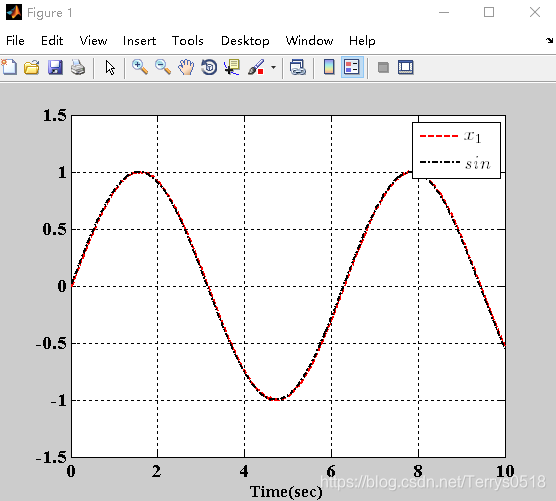
sin为原信号，x₁为跟踪信号。

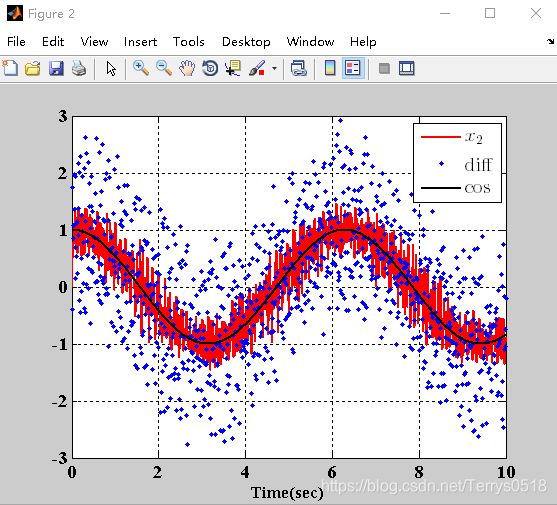
cos为理想信号，x₂为微分跟踪信号，diff为用简单差分计算出的微分信号。

仿真 r = 10 T=0.01

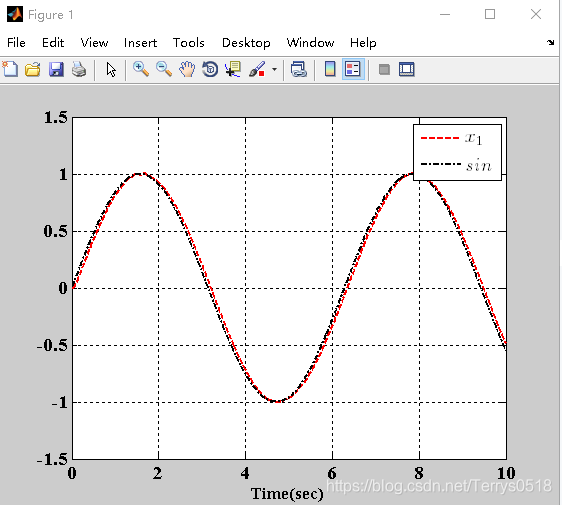
sin为原信号，x₁为跟踪信号。

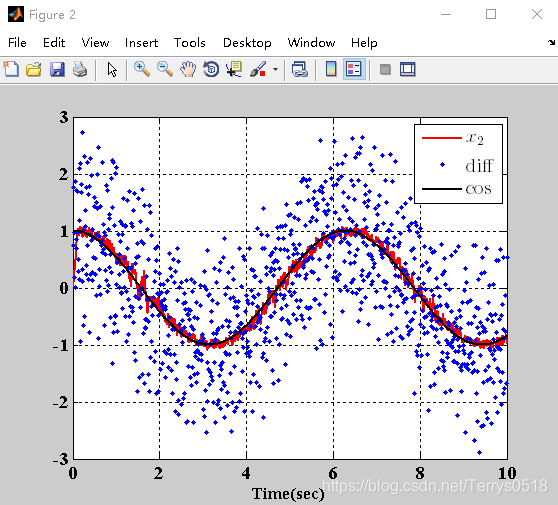
cos为理想信号，x₂为微分跟踪信号，diff为用简单差分计算出的微分信号。

仿真 r = 100 T=0.01 对阶跃信号 10u(t-5)的仿真

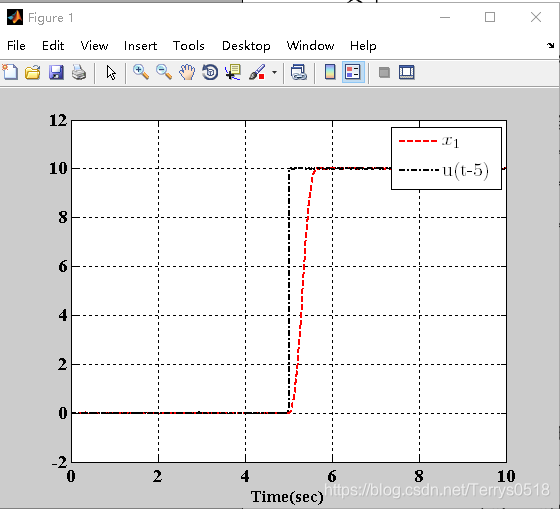
简单结论

相比于原来的 一般差分计算微分的方法，使用微分跟踪器能有效抑制测量信号的噪声干扰，而且零点不产生振荡，也方便调节。
以上信号的分析可得，跟踪效果要好，R要大，但R过大会给微分信号增加高频噪声。
离散微分器可方便改写成C语言，可广泛用于PID控制，信号滤波等场合

[1]:《《非线性跟踪器-微分器》 韩京清 王伟 著》
[2]:https://blog.csdn.net/miracle_fans/article/details/78223203

这篇关于非线性跟踪-微分器 仿真应用的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---