在没有康托尔对角化方法的情况下证明实数的不可数性

一、说明

        对于那些对数学感兴趣的人来说，无穷大实际上可以有不同的大小，这可能是一个众所周知的事实。事实上，最著名的例子是所有实数的集合比所有自然数的集合“大”。你可能知道，这实际上有一个非常优雅的证明，称为康托尔对角线方法，由乔治·康托尔在1891年提出。如果您不知道这一点，我绝对建议您研究一下，因为我认为该方法非常聪明，但同时任何人都很容易理解。

        然而，在这篇文章中，呈述通过一种稍微严格的方法来证明实数是不可数的，这种方法涉及集合的概念。虽然我不会声称这是完全严格的，但我确实发现这仍然是解决这个问题的一种非常有趣的方法。     

        此外，在这篇文章中，我将假设对集合是什么以及集合之间的交集意味着什么有一个基本的了解。

二、嵌套间隔属性

        在继续之前，我想介绍一个重要的定理，称为嵌套区间属性，它将用于证明实数是不可数的。嵌套间隔属性声明如下：

对于每个 n ∈ N，假设我们给定一个区间 In = [an， bn] = {x ∈ R ： 一个< x < bn}。 还假设每个间隔包含下一个（即 In ⊆...⊆ I₂⊆ I₁）。然后，这个嵌套的区间序列将有一个非空的交集。

        在数学上，我们可以将结果表示如下：

        为了更轻松地解释嵌套间隔属性，请考虑实数上的任何间隔，并将其设为 I₁。现在考虑在该区间内新建一个区间，并将其设为 I₂。现在一遍又一遍地重复这个过程。因此，您将获得如下所示的嵌套间隔：

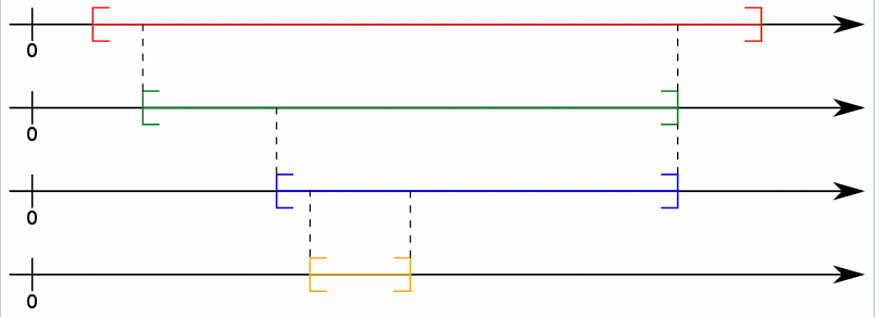
        嵌套间隔 |图片来源：维基百科

        嵌套间隔属性声称所有这些间隔的交集都是非空的，我们能够找到一些 x ∈ I₁⋂I₂⋂...⋂无论n有多大。虽然可以通过引入其他公理和概念来提供嵌套间隔属性的证明，但为了这篇文章，我会认为这是理所当然的。

三、实数的不可数性

        配备嵌套间隔属性，我们可以尝试证明实数确实是不可数的。首先，让我们首先考虑“可数”的真正含义。

        如果集合 A 与自然数 N 有 1-1 的对应关系，则认为它是可数的。简单来说，如果 A 与 N 有 1-1 的对应关系，这意味着我们可以找到一个函数 f ： N → A，使得 N 中的每个元素正好对应于 A 中的一个元素，反之亦然（稍微具体的解释是 f 是 1-1 和 onto）。另一种说明方式是，A 中的每个元素都可以使用自然数进行编号。

        了解了集合可数的含义后，我们现在可以开始证明了。对于这个证明，我们将使用矛盾证明的方法，首先假设实数实际上是可数的。这意味着 N 和 R 之间实际上存在 1-1 的对应关系，由某个函数 f ： N →R 给出。换句话说，我们能够枚举实数，我们可以通过让 xn = f（n） 来表示实数，为 R 给出以下表达式：

        因此，我们使用自然数枚举了 R 的每个元素。这就是嵌套间隔属性发挥作用的地方。

        首先，让 I₁ 是 R 上不包含 x₁ 的闭区间。在此之后，我们将构造剩余的嵌套间隔 In，它们具有以下属性：

        要解释这意味着什么，请考虑 I₂。由于第一个属性，I₂ 是 I₁ 的子集，由于第二个属性，x₂ 不在 I₂ 中。 对 I₃、I₄ 等重复此操作。请注意，应该直观地理解为什么这样的区间序列是可能的，因为给定某个区间，只需简单地避免该数字，就不难创建嵌套在该区间中不包含特定实数的另一个区间。

        现在，考虑我们刚刚构建的所有这些区间之间的交集。如果我们在上面的枚举实数列表中包含一些实数 xm，那么我们知道它不会是第 m 个区间 Im 的一个元素，因为这些区间的上述属性。因此，我们可以得出以下结论：

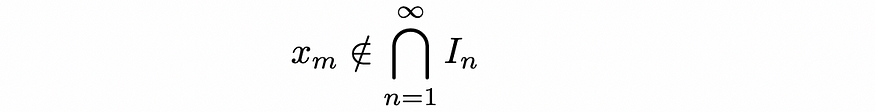
        但是，嵌套间隔属性告诉我们，这些嵌套间隔的交集必须是非空的，并且我们能够找到一些 x，例如：

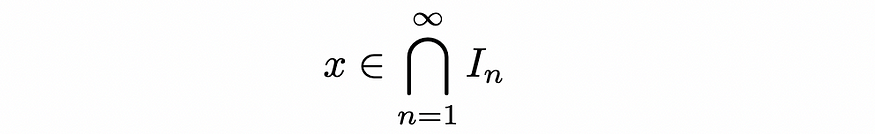
        但是通过这些区间的性质，我们知道这个新发现的x不能出现在我们在假设中创建的实数枚举列表中。因此，我们有一个明显的矛盾，并且可以得出结论，我们关于R是可数的假设一定是假的，这表明R确实是不可数的。

        虽然这种使用区间的相当抽象的方法肯定不如康托尔的对角线化方法直观，但我认为看到一种更严格的方法涉及从实际分析中理解集合和函数是相当有启发性的。但是，这个证明肯定仍然存在缺陷，我没有完全解释的事情，所以如果你有兴趣，我肯定会建议你多读一读。我使用的这个特殊证明改编自雅培的理解分析（下面引用），这是我推荐阅读的一本很棒的教科书，其中还包括我跳过的嵌套间隔属性的证明。感谢您的阅读。

四、引用

雅培，S.（2016）。了解分析。斯普林格。

坂本健成