本文主要是介绍小波变换在数字图像上的应用(上),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
小波变换在数字图像上的应用(上)
小波变换原理的简单概述
一维小波变换
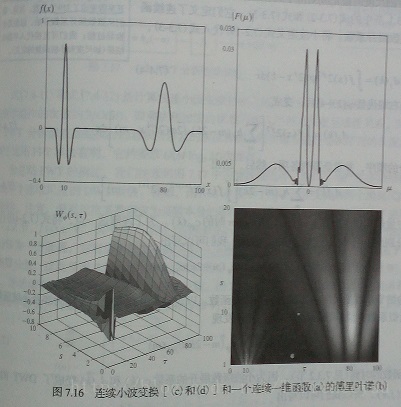
- 关于一维连续小波和离散小波变换的公式只能抱书啃了,这里给出一张图展示小包变换分析的一些特点。
- 第一幅图是原始信号,其右侧是它的傅里叶谱,由傅里叶谱我们可以知道原始信号存在两个频率峰值。但是关于这两个频率峰值出现的时间却无法得知。
- 也许你觉得短时傅里叶变换可以解决这个问题,实际上关于STFT窗宽的选择存在一个矛盾。选择的框太宽时间分辨率差,选择的框太窄频率分辨率就差。
- 而通过上图下面两张小波变换得到的谱图,我们可以得到非常准确的空间域和频率域的信息。
FWT
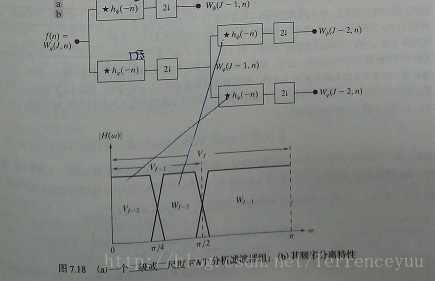
快速小波变换的过程可以表示为下图所示。
- 根据FWT的公式所知,求小波系数,实际上是求一个非负的偶数项的卷积,而非负的偶数项求卷积等价于滤波和基2下取样。
- 这个过程如上图所示,可求得一个近似分量(低通)和一个高通。再对这个低通求一个尺度的滤波和下采样,可再次求得一个低通和一个高通。经此两过程求得的频率成分对应于上图下侧。
二维快速小波变换
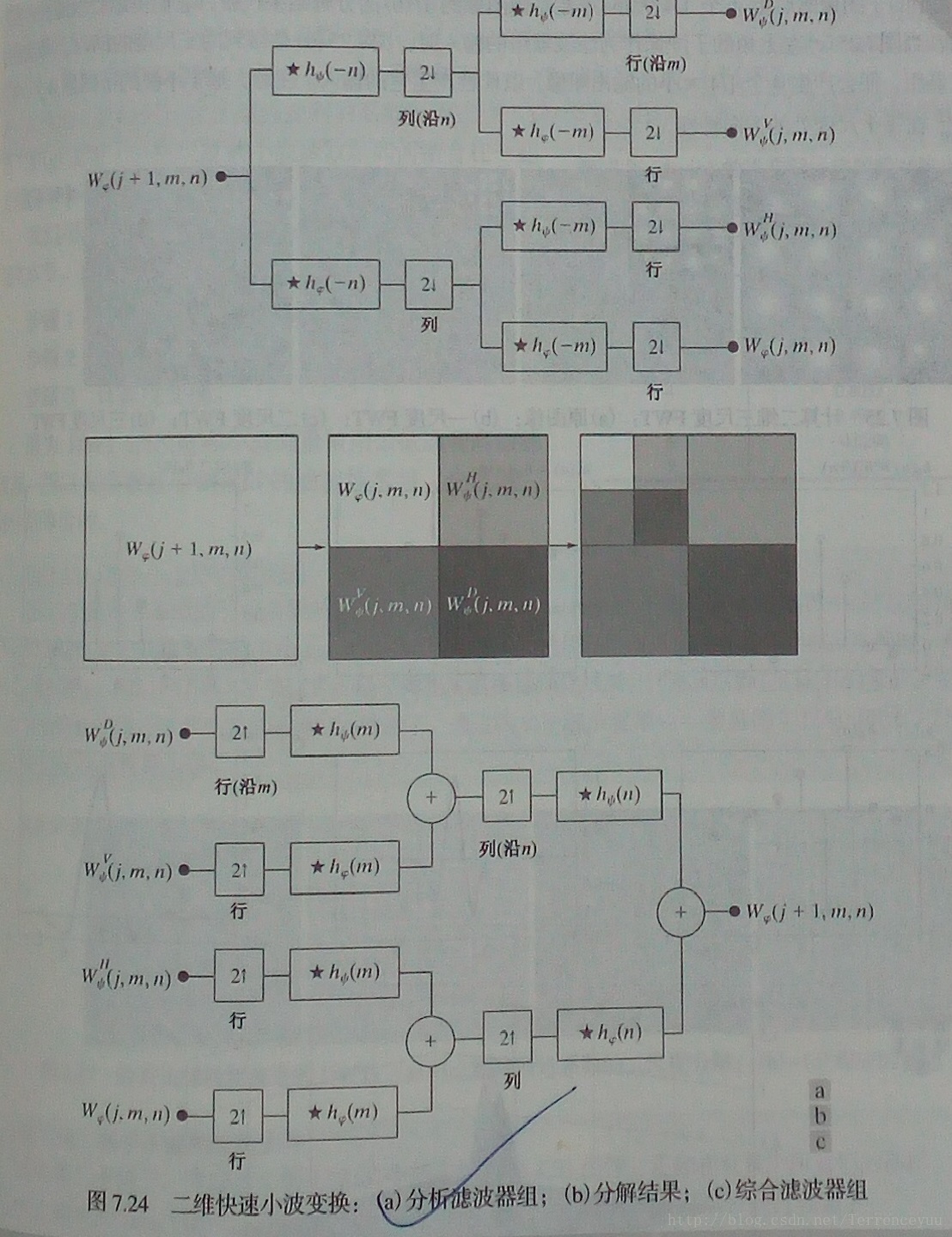
- 小波变换扩展到二维和傅里叶变换扩展到二维有些类似,除了产生一个二维的尺度函数还产生了三个方向敏感的小波(分别是水平,垂直,和对角线)。
- 二维的快速小波变换和逆变换过程也可以表示为下图。
- 上图最上侧最后得到的四个分量依次是对角线细节分量,垂直细节分量,水平细节分量和近似分量。
小波包
- 根据以上分析我们知道,FWT的分解是多样的。那么如何分解才能够具有一个比较好的效果呢?这时候就需要介绍小波包。
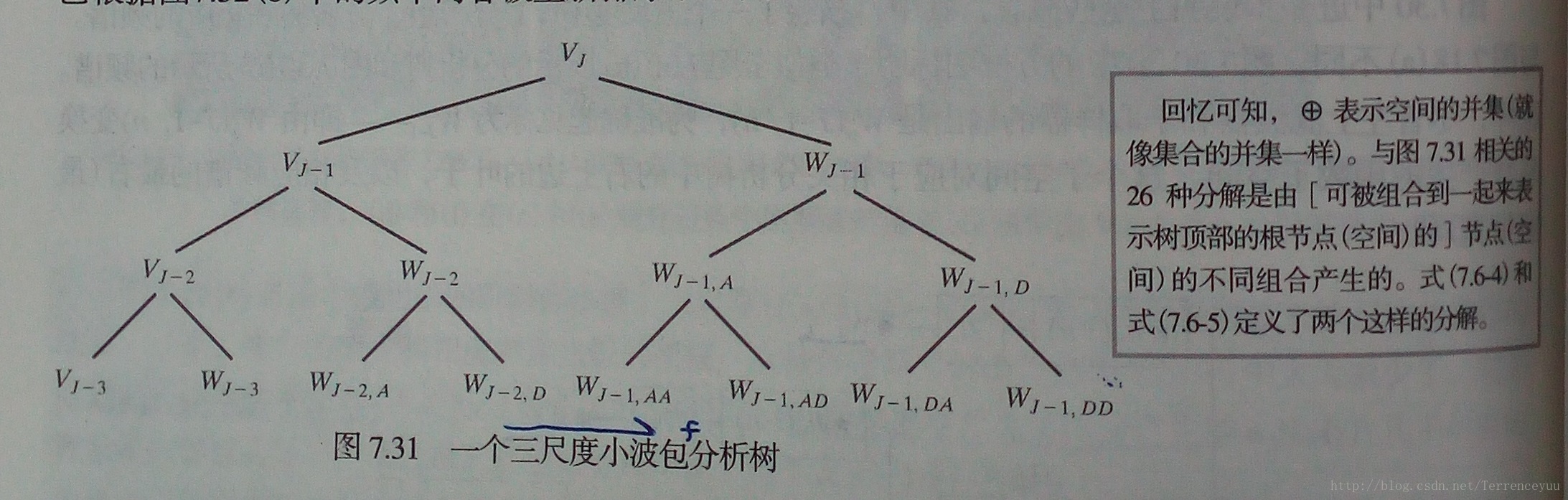
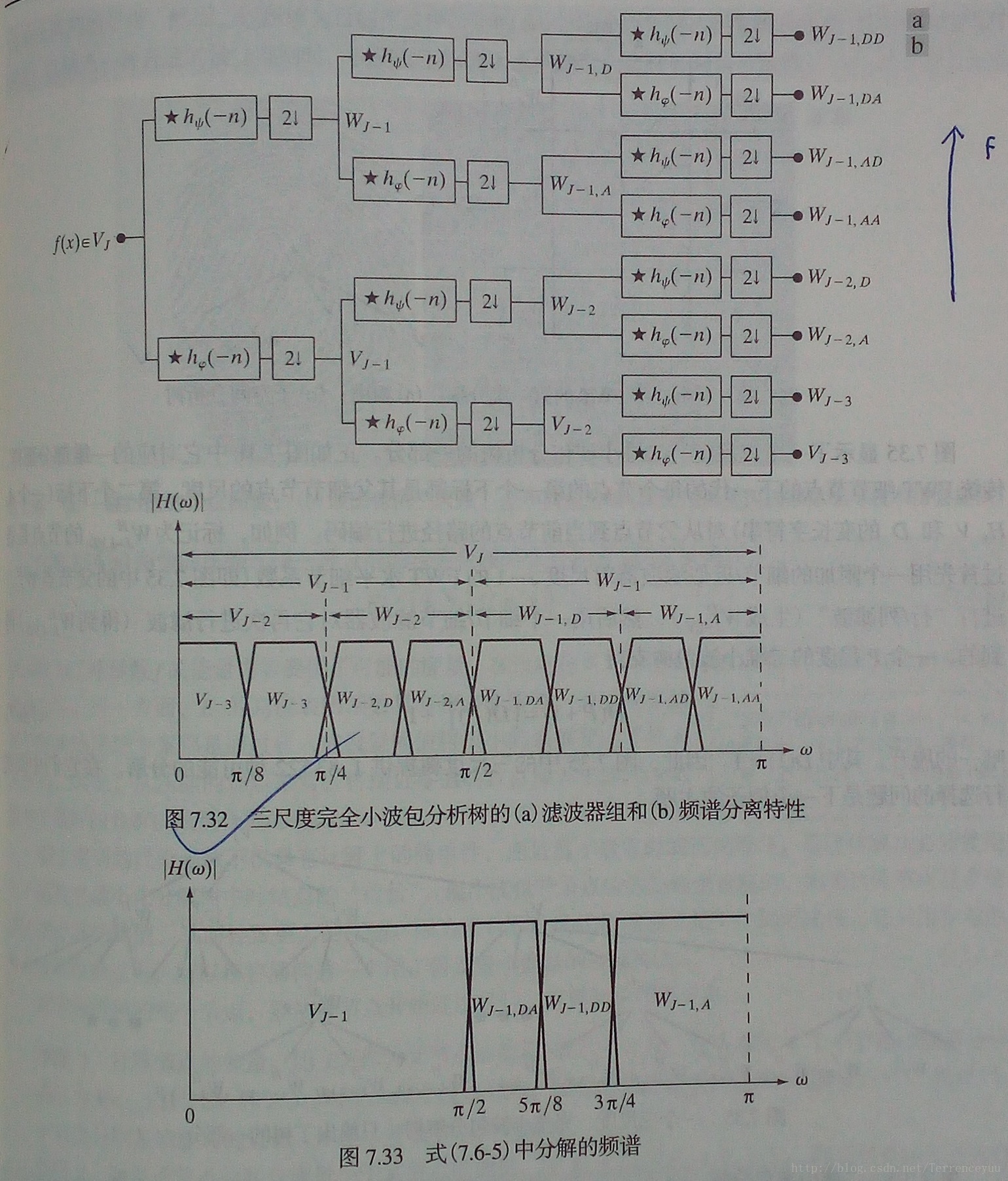
小波包类似一个二叉树。下图展示了一个三尺度的小波包。
下图展示经此小波包分解的过程及最终得到的频率分离特性。
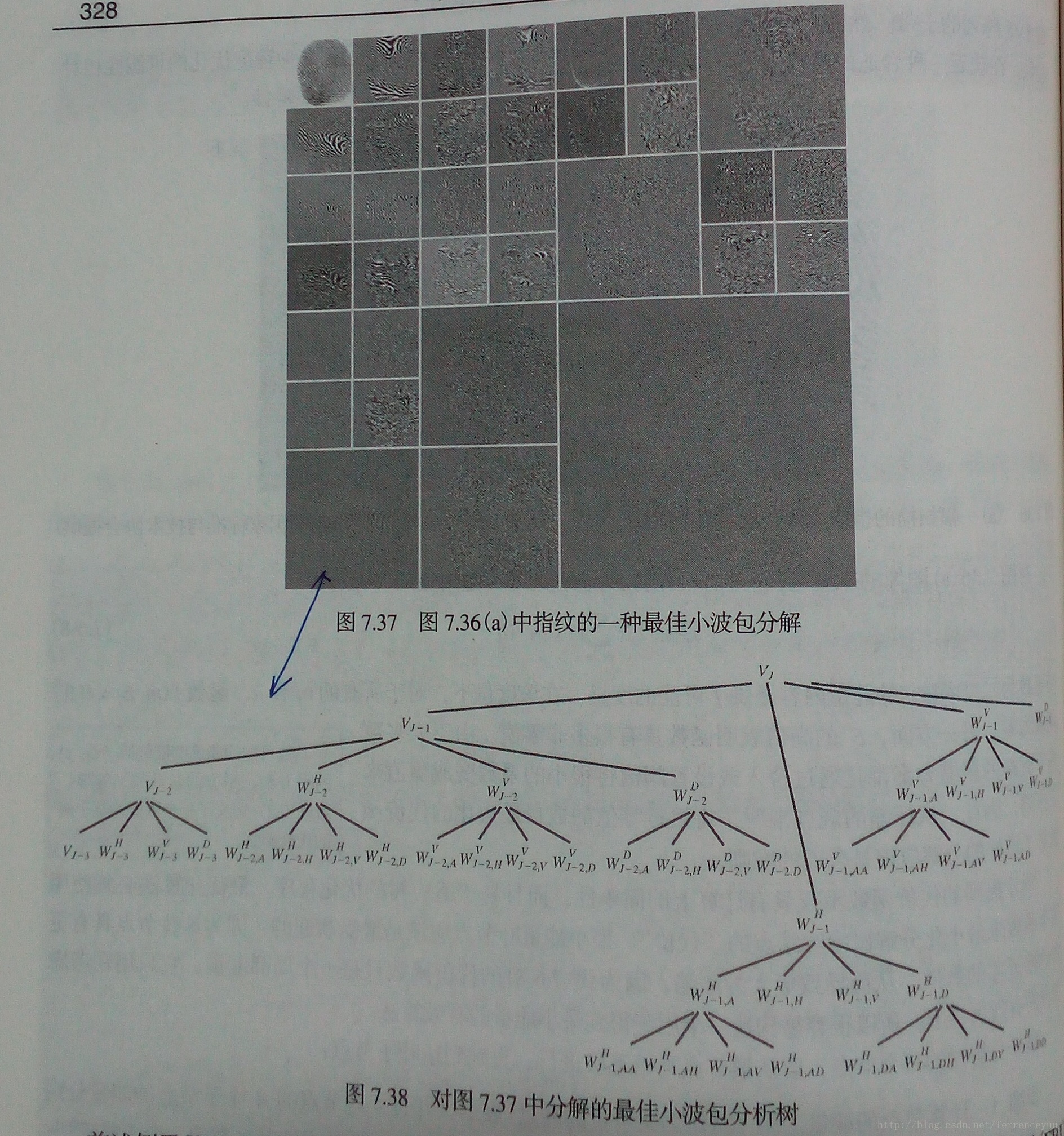
最后,展示一副指纹图像经过小波包分解的效果。
这篇关于小波变换在数字图像上的应用(上)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!