本文主要是介绍LeetCode:2617. 网格图中最少访问的格子数(优先级队列 Java),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
2617. 网格图中最少访问的格子数
题目描述:
实现代码与解析:
优先级队列
原理思路:
2617. 网格图中最少访问的格子数
题目描述:
给你一个下标从 0 开始的 m x n 整数矩阵 grid 。你一开始的位置在 左上角 格子 (0, 0) 。
当你在格子 (i, j) 的时候,你可以移动到以下格子之一:
- 满足
j < k <= grid[i][j] + j的格子(i, k)(向右移动),或者 - 满足
i < k <= grid[i][j] + i的格子(k, j)(向下移动)。
请你返回到达 右下角 格子 (m - 1, n - 1) 需要经过的最少移动格子数,如果无法到达右下角格子,请你返回 -1 。
示例 1:

输入:grid = [[3,4,2,1],[4,2,3,1],[2,1,0,0],[2,4,0,0]] 输出:4 解释:上图展示了到达右下角格子经过的 4 个格子。
示例 2:
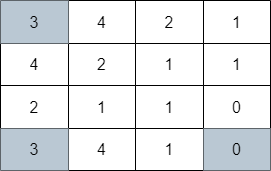
输入:grid = [[3,4,2,1],[4,2,1,1],[2,1,1,0],[3,4,1,0]] 输出:3 解释:上图展示了到达右下角格子经过的 3 个格子。
示例 3:
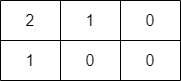
输入:grid = [[2,1,0],[1,0,0]] 输出:-1 解释:无法到达右下角格子。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 1051 <= m * n <= 1050 <= grid[i][j] < m * ngrid[m - 1][n - 1] == 0
实现代码与解析:
优先级队列
import java.util.Arrays;
import java.util.PriorityQueue;class Solution {public int minimumVisitedCells(int[][] grid) {int n = grid.length, m = grid[0].length;int[][] d = new int[n][m]; // 到每个单元格的步数// 初始化for (int i = 0; i < n; i++) {Arrays.fill(d[i], -1);}// int[0] 步数 int[1] 行或列号,行堆存的列号,列堆存的行号,确定位置PriorityQueue<int[]>[] pqrs = new PriorityQueue[n]; // pq rowsPriorityQueue<int[]>[] pqcs = new PriorityQueue[m]; // pq colsfor (int i = 0; i < n; i++) {pqrs[i] = new PriorityQueue<>((a, b) -> a[0] - b[0]); // 小根堆,按到该位置的步数}for (int i = 0; i < m; i++) {pqcs[i] = new PriorityQueue<>((a, b) -> a[0] - b[0]);}d[0][0] = 1; // 起始for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {// 行// 不能到i, j的弹出直接,因为不能一步到,剩下的同行格更不可能一步到while (!pqrs[i].isEmpty() && grid[i][pqrs[i].peek()[1]] + pqrs[i].peek()[1] < j) {pqrs[i].poll();}// 如果最后行堆中有剩余,堆顶就是我们当前单元格的一个方向的答案,比较取最小,当然在-1时直接赋值即可if (!pqrs[i].isEmpty()) {d[i][j] = d[i][j] == -1 || d[i][pqrs[i].peek()[1]] + 1 < d[i][j] ? d[i][pqrs[i].peek()[1]] + 1 : d[i][j];}// 列while (!pqcs[j].isEmpty() && pqcs[j].peek()[1] + grid[pqcs[j].peek()[1]][j] < i) {pqcs[j].poll();}if (!pqcs[j].isEmpty()) {d[i][j] = d[i][j] == -1 || d[pqcs[j].peek()[1]][j] + 1 < d[i][j] ? d[pqcs[j].peek()[1]][j] + 1 : d[i][j];}// 如果可以到达,加入到堆中if (d[i][j] != -1) {pqrs[i].offer(new int[]{d[i][j], j});pqcs[j].offer(new int[]{d[i][j], i});}}}return d[n - 1][m - 1];}
}原理思路:
其实就是dp,只不过这里走的条件是和格内值和位置决定,所有需要额外数据结构来维护。
进行遍历,由于只能从左和上而来,所以我们正常从左向右遍历,为了找出可以到达i,j的格子,我们用优先级队列(小堆)来维护每一行和每一列,里面存放两个值,一个到i,j的步数(用于堆的排序,),一个为单元格内的值d[i][j](用于判断能否到达当前单元格)。
开始遍历,拿行举例,先把行堆内不能到达该单元格的弹出,因为如果不能一步到达,说明至少需要两步,而左侧单元格已经进行计算过了,如果两步可以到达当前单元格,那么前面一定存在可以一步到达的单元格(不过不一定是该答案,因为也许有比它步数还小的把这个单元格更新了,当然它肯定在堆中),所以直接弹出即可。
如果最后堆中都被弹出了,说明在水平方向,无法到达该单元格,如果还有元素,堆顶就是该单元格行方向上的最小步数(小顶堆),进行比较取小的然后更新。因为我们初始化-1为不能到达,所以如果单元格内为-1,就不比较了,直接赋值。
列也同理。最后把当前单元格信息放入堆中为后面的单元格更新作为条件即可。
最后求出d[n -1][m-1]。
这篇关于LeetCode:2617. 网格图中最少访问的格子数(优先级队列 Java)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









