本文主要是介绍【机器学习】机器学习实验方法与原则(统计有效性检验详解),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
统计有效性检验
假设的评估检验:问题1
• 效果估计
• 给定一个假设 在有限量数据 上的准确率
• 该准确率是否能准确估计 在其它未见数据上 的效果?

假设的评估检验:问题2
• h 1 在数据的一个样本集上表现优于 h 2
• h 1 总体 上更好的概率有多大?
抽样理论基础

二项分布 (Binomial Distribution)
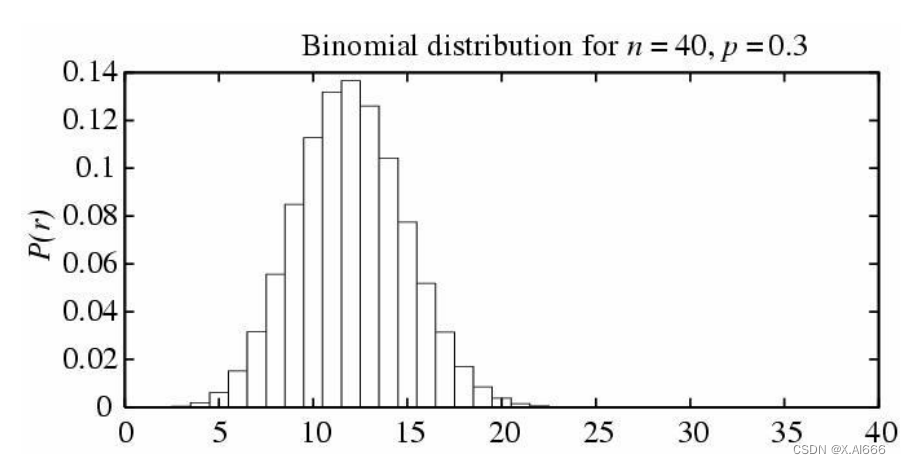
二项分布的应用场景
• 两个可能的输出 ( 成功 / 失败 ) ( Y =0 或 Y =1)
• 每次尝试成功的概率相等 Pr ( Y = 1) = p , 其中 p 是一个常数
• n 次独立尝试
• 随机变量 Y 1 ,…, Y n ,
• iid (independent identically distribution ,独立同分布 )
• R : 随机变量 , n 次尝试中 Y i = 1 的次数 ,
• Pr(R = r ) ~ 二项分布
• 平均 ( 期望值 ): E [ R ], µ
• 二项分布 : µ = np

估计假设准确率 – Q1.1解答

估计的两个重要性质
• 估计 偏差 (Bias)
• 如果 S 是训练集, errorS ( h ) 是有偏差的(偏乐观),
bias ≡ E[ error S ( h ) ] - error D ( h )
• 对于无偏估计( bias =0), h 和 S 必须独立不相关地产生
→ 不要在训练集上测试!
• 估计 方差 (Varias)
• 即使是 S 的无偏估计, error S ( h ) 可能仍然和 error D ( h ) 不同
• E.g. 之前的例子 (3.2% vs. 6.5%)
• 需要选择 无偏 的且有 最小方差 的估计
估计假设准确率 – Q1.2解答
准确率的估计可能包含多少错误?
( error S ( h ) 对 error D ( h ) 的估计有多好 ?)
• 抽样理论 : confidence interval ( 置信区间 )
• 定义 :
• 参数 p 的 N % 置信区间是一个以 N % 的概率包含 p 的区间 , N % : 置信度
✓ 90.0% 的置信度 ,年龄: [12, 24]
✓ 99.9% 的置信度,年龄: [3, 60]
置信度与置信区间
• 如何得到置信区间 ?
• 坏消息 : 对二项分布来说很难
• 好消息 : 对正态分布来说很简单
• 通过正态分布的某个区间
(面积)来获得
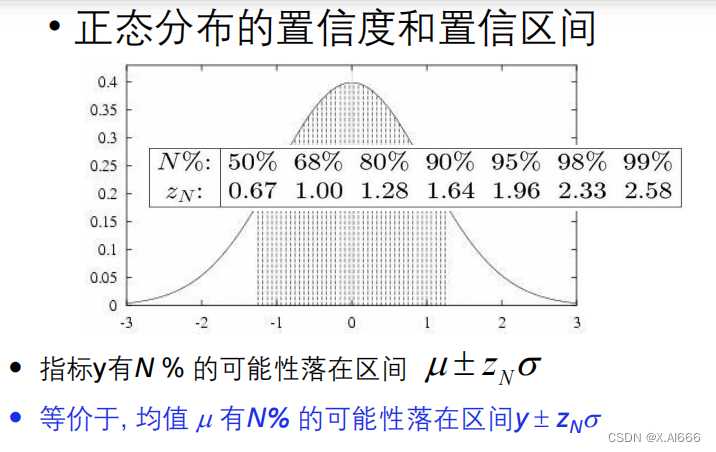

正态分布 & 二项分布
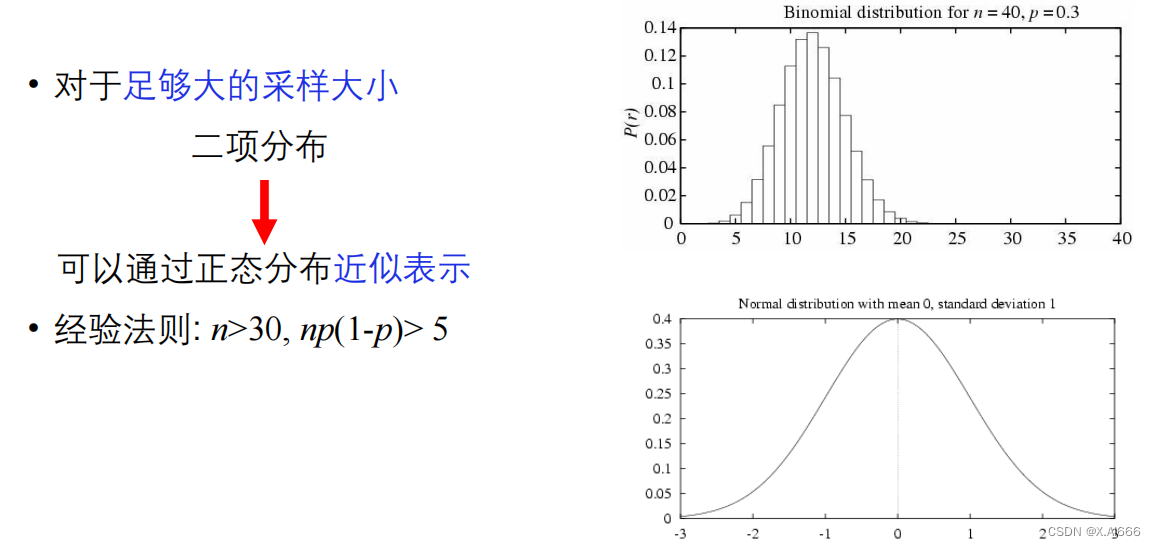
• 如果满足以下条件,估计更准确:
• S 包含 n >= 30 个样本 , 与 h 独立产生,且每个样本独立采样
• 那么有大约 95% 的概率 𝑒𝑟𝑟𝑜𝑟 𝑆 (ℎ) 落在区间

问题1解答总结
• 问题设定 :
• S : n 随机独立 样本 , 且 独立于假设 h
• n >= 30 & h 有 r 个错误
• 真实错误率 error D 落在以下区间有 N % 置信度 :

推导置信区间的一般方法

中心极限定理
• 简化了求解置信区间的过程
• 问题设定
• 独立同分布Independent, identically distributed (iid)
的随机变量Y1 , .. , Y n ,
• 未知分布 , 有均值 μ 和有限方差 σ 2
• 估计均值: 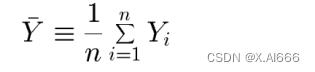
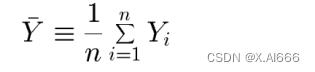

样本均值 的分布 是已知的 , 即使 Y i 的分布是未知的
可以用来确定的 Y i 均值方差
提供了估计的基础
估计量的分布
一些样本的均值
假设间的差异
• 在样本集合 S 1 ( n 1 个随机样本 ) 上测试 h 1 , 在 S 2 ( n 2 ) 上测试 h 2
• 选择要估计的参数 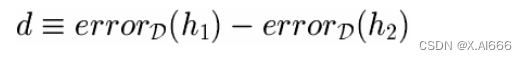
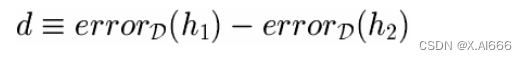
• 选择估计量
• 无偏的 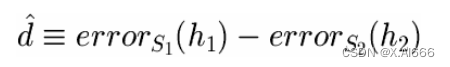
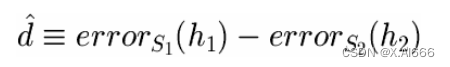

* 证明 : http://en.wikipedia.org/wiki/Sum_of_normally_distributed_random_variables
• 在样本集合 S 1 ( n 1 个随机样本 ) 上测试 h 1 , 在 S 2 ( n 2 ) 上测试 h 2
• 选择要估计的参数 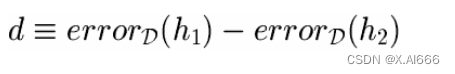
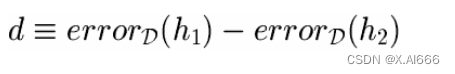
• 选择估计量
• 无偏的 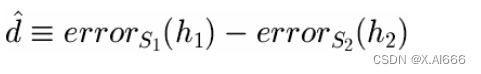
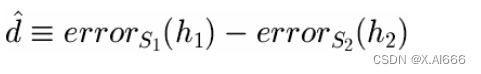
• 确定估计量所服从的正态分布

• 确定区间 ( L , U ) 满足 N % 的概率落在区间

假设检验

统计有效性检验: ( z检验)举例


统计有效性检验:t检验

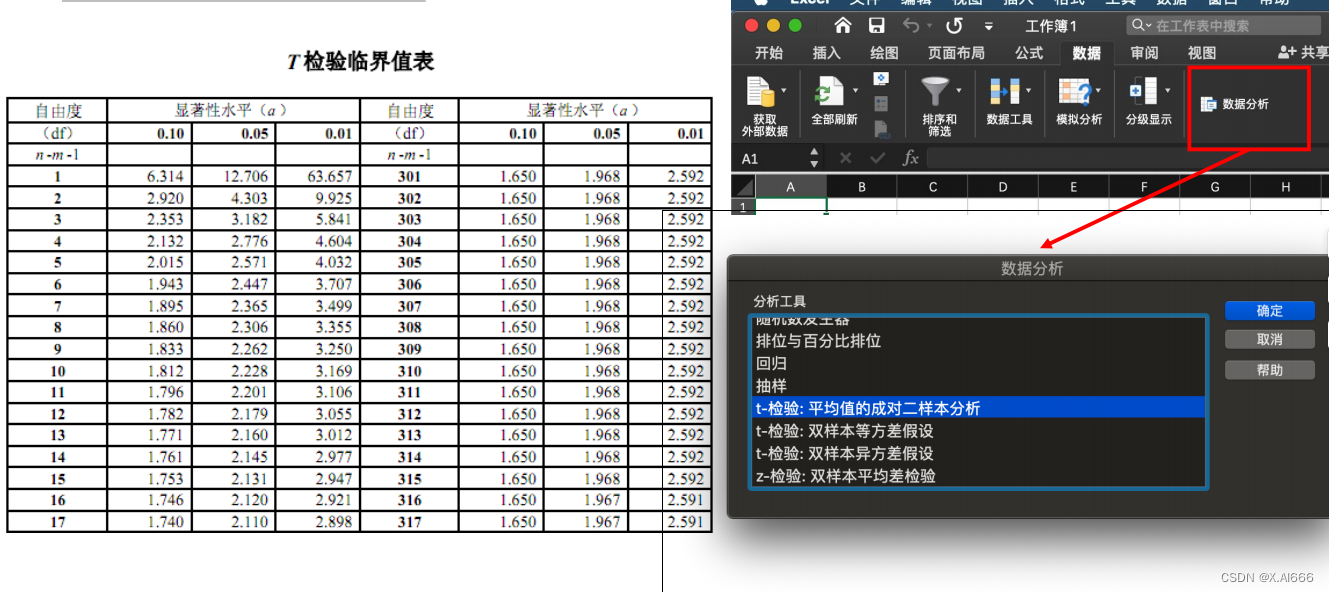
统计有效性检验(总结)
• 比较算法 A 和 B 的优劣
• 准确率均值高就一定好? 有随机性
• A比 B 高多少才能有把握说 A 算法更好? 显著性检验
• 随机变量的样本个数较多时 ( 一般 >30) : z 检验 ( 利用中心极限定理 )
• 一般用于单次评测,随机变量为 每个测试样本 的对错
• 随机变量的样本个数较少时 ( 一般 <=30) : t 检验
• 一般用于多次评测如重复实验,随机变量为 每次测试集 上的指标
这篇关于【机器学习】机器学习实验方法与原则(统计有效性检验详解)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



