本文主要是介绍c# 三元搜索 - 迭代与递归(Ternary Search),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
计算机系统使用不同的方法来查找特定数据。有多种搜索算法,每种算法更适合特定情况。例如,二分搜索将信息分为两部分,而三元搜索则执行相同的操作,但分为三个相等的部分。值得注意的是,三元搜索仅对排序数据有效。在本文中,我们将揭开三元搜索的秘密——它是如何工作的,为什么它在某些情况下更快。无论您是编码专家还是刚刚起步,都准备好快速进入三元搜索的世界!
什么是三元搜索?
三元搜索是一种搜索算法,用于查找排序数组中目标值的位置。它的工作原理是将数组分为三部分,而不是像二分搜索那样分为两部分。基本思想是通过将目标值与将数组分为三个相等部分的两个点上的元素进行比较来缩小搜索空间。
mid1 = l + (rl)/3
mid2 = r – (rl)/3
三元搜索的工作原理:
这个概念涉及将数组分成三个相等的段,并确定关键元素(正在寻找的元素)位于哪个段。它的工作原理与二分搜索类似,不同之处在于通过将数组分为三部分而不是两部分来降低时间复杂度。
以下是三元搜索工作的分步说明:
1、初始化:
从排序数组开始。
设置两个指针left和right,最初指向数组的第一个和最后一个元素。
2、划分数组:
计算两个中点mid1和mid2,将当前搜索空间分为三个大致相等的部分:
mid1 = 左 + (右 – 左) / 3
mid2 = 右 – (右 – 左) / 3
该数组现在有效地分为[left, mid1]、(mid1, mid2 ) 和[mid2, right]。
3、与目标比较: .
如果target等于mid1或mid2处的元素,则查找成功,并返回索引
如果目标小于mid1处的元素,则将右指针更新为mid1 – 1。
如果目标大于mid2处的元素,则将左指针更新为mid2 + 1。
如果目标位于mid1和mid2的元素之间,则将左指针更新为mid1 + 1,将右指针更新为mid2 – 1。
4、重复或结论:
使用缩小的搜索空间重复该过程,直到找到目标或搜索空间变空。
如果搜索空间为空并且未找到目标,则返回一个值,指示目标不存在于数组中。
插图:
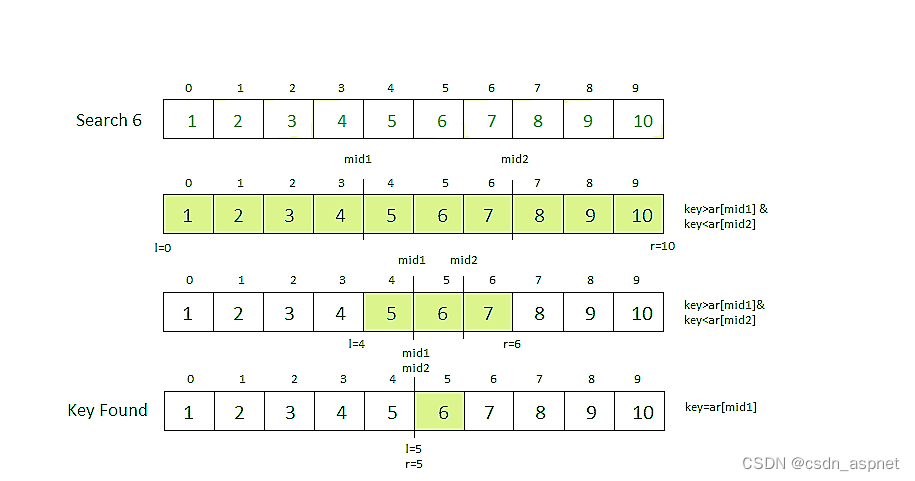
三元搜索的递归实现:
// CSharp program to illustrate
// recursive approach to ternary search
using System;
class GFG {
// Function to perform Ternary Search
static int ternarySearch(int l, int r, int key, int[] ar)
{
if (r >= l) {
// Find the mid1 and mid2
int mid1 = l + (r - l) / 3;
int mid2 = r - (r - l) / 3;
// Check if key is present at any mid
if (ar[mid1] == key) {
return mid1;
}
if (ar[mid2] == key) {
return mid2;
}
// Since key is not present at mid,
// check in which region it is present
// then repeat the Search operation
// in that region
if (key < ar[mid1]) {
// The key lies in between l and mid1
return ternarySearch(l, mid1 - 1, key, ar);
}
else if (key > ar[mid2]) {
// The key lies in between mid2 and r
return ternarySearch(mid2 + 1, r, key, ar);
}
else {
// The key lies in between mid1 and mid2
return ternarySearch(mid1 + 1, mid2 - 1, key, ar);
}
}
// Key not found
return -1;
}
// Driver code
public static void Main()
{
int l, r, p, key;
// Get the array
// Sort the array if not sorted
int[] ar = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
// Starting index
l = 0;
// end element index
r = 9;
// Checking for 5
// Key to be searched in the array
key = 5;
// Search the key using ternarySearch
p = ternarySearch(l, r, key, ar);
// Print the result
Console.WriteLine("Index of " + key + " is " + p);
// Checking for 50
// Key to be searched in the array
key = 50;
// Search the key using ternarySearch
p = ternarySearch(l, r, key, ar);
// Print the result
Console.WriteLine("Index of " + key + " is " + p);
}
}
// This code is contributed by Ryuga
输出
5 的指数为 4
50 的指数为 -1
时间复杂度: O(2 * log 3 n)
辅助空间: O(log 3 n)
三元搜索的迭代方法:
// C# program to illustrate the iterative
// approach to ternary search
using System;
public class GFG {
// Function to perform Ternary Search
static int ternarySearch(int l, int r,
int key, int[] ar)
{
while (r >= l) {
// Find the mid1 and mid2
int mid1 = l + (r - l) / 3;
int mid2 = r - (r - l) / 3;
// Check if key is present at any mid
if (ar[mid1] == key) {
return mid1;
}
if (ar[mid2] == key) {
return mid2;
}
// Since key is not present at mid,
// check in which region it is present
// then repeat the Search operation
// in that region
if (key < ar[mid1]) {
// The key lies in between l and mid1
r = mid1 - 1;
}
else if (key > ar[mid2]) {
// The key lies in between mid2 and r
l = mid2 + 1;
}
else {
// The key lies in between mid1 and mid2
l = mid1 + 1;
r = mid2 - 1;
}
}
// Key not found
return -1;
}
// Driver code
public static void Main(String[] args)
{
int l, r, p, key;
// Get the array
// Sort the array if not sorted
int[] ar = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
// Starting index
l = 0;
// end element index
r = 9;
// Checking for 5
// Key to be searched in the array
key = 5;
// Search the key using ternarySearch
p = ternarySearch(l, r, key, ar);
// Print the result
Console.WriteLine("Index of " + key + " is " + p);
// Checking for 50
// Key to be searched in the array
key = 50;
// Search the key using ternarySearch
p = ternarySearch(l, r, key, ar);
// Print the result
Console.WriteLine("Index of " + key + " is " + p);
}
}
// This code has been contributed by 29AjayKumar
输出
5 的指数为 4
50 的指数为 -1
时间复杂度: O(2 * log 3 n),其中 n 是数组的大小。
辅助空间: O(1)
三元搜索的复杂度分析:
时间复杂度:
最坏情况:O(log 3 N)
平均情况: θ(log 3 N)
最好的情况:Ω(1)
辅助空间: O(1)
二元搜索与三元搜索:
二分查找的时间复杂度低于三目查找,因为三目查找的比较次数比二分查找多得多。二分搜索用于查找单调函数的最大值/最小值,而三元搜索用于查找单峰函数的最大值/最小值。
注意:我们也可以对单调函数使用三元搜索,但时间复杂度会比二分搜索稍高。
优点:
三元搜索可以找到单峰函数的最大值/最小值,而二元搜索不适用。
三元搜索的时间复杂度为O(2 * log 3 n),比线性搜索更高效,与二分搜索相当。
非常适合优化问题。
缺点:
三元搜索仅适用于有序列表或数组,不能用于无序或非线性数据集。
与二元搜索相比,三元搜索需要更多时间来查找单调函数的最大值/最小值。
何时使用三元搜索:
当您有一个大型有序数组或列表并且需要查找特定值的位置时。
当您需要找到函数的最大值或最小值时。
当您需要在双调序列中找到双调点时。
当您必须计算二次表达式时
概括:
三元搜索是一种分治算法,用于查找给定数组或列表中特定值的位置。
它的工作原理是将数组分为三部分,并对适当的部分递归地执行搜索操作,直到找到所需的元素。
该算法的时间复杂度为 O(2 * log 3 n),比线性搜索更有效,但比二分搜索等其他搜索算法不太常用。
需要注意的是,要使三元搜索正常工作,要搜索的数组必须进行排序。
这篇关于c# 三元搜索 - 迭代与递归(Ternary Search)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



