从零开始学习深度学习库-4：自动微分

本文主要是介绍从零开始学习深度学习库-4：自动微分，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

欢迎来到本系列的第四部分，在这里我们将讨论自动微分

介绍

自动微分（Automatic Differentiation，简称AD）是一种计算数学函数导数（梯度）的技术。在深度学习和其他领域中，自动微分是一种极其重要的工具，特别是在梯度下降这类优化算法中。不同于数值微分和符号微分，自动微分以一种高效和精确的方式计算导数。

自动微分的关键特点包括：

1.计算图: 自动微分通常通过构建一个计算图来实现，这个图包含了原始函数的所有操作。在这个图中，每个节点代表一个操作（如加法、乘法等），而边代表数据（如变量、常数）之间的依赖关系。

2.前向传播与反向传播: 在计算图中，自动微分主要有两种模式：前向模式（Forward mode）和反向模式（Reverse mode）。前向模式适用于输入变量少的情况，而反向模式（也被称为反向传播算法）在深度学习中更为常用，特别是当输出变量少而输入变量多的时候。

3.链式法则: 自动微分的核心是链式法则，它允许从复合函数的内部函数开始，逐步计算每一部分的导数，最终得到整个复合函数的导数。在反向模式下，这个过程从输出开始，沿着计算图向输入方向进行。

4.高效与精确: 与数值微分相比，自动微分不仅计算速度更快，而且避免了数值稳定性问题。与符号微分不同，它不会产生复杂的中间表达式，因此更加高效。

简单来说，一个函数对于某个变量的导数衡量了该函数的结果随变量改变而发生的变化量。它本质上衡量了函数对于该变量变化的敏感度。这是训练神经网络的一个重要部分。

到目前为止，在我们的库中，我们一直手动计算变量的导数。然而，在实际中，深度学习库依赖于自动微分。

自动微分是通过代码表达的任何数值函数的导数精确计算的过程。

更简单地说，对于我们在代码中进行的任何计算，我们应该能够计算出该计算中使用的任何变量的导数。

...
y = 2*x + 10
y.grad(x) #what is the gradient of x???
...

正向模式自动微分与反向模式自动微分

自动微分有两种流行的方法：正向模式和反向模式。

正向模式利用双数来计算导数。

双数是任何形式的数…
$x=a+bϵ$
这里$ϵ$是一个非常接近0的数字，因此${ϵ}^2=0$
如果我们对双数应用一个函数，如下所示…

$f(x)=f(a+bϵ)=f(a)+(f^{\prime }(a)\cdot b)ϵ$

你可以看到我们既计算了 $f(a)$ 的结果，也计算了 $a$ 的梯度，梯度由 $ϵ$ 的系数给出。

当输入维度小于函数的输出维度时，更倾向于使用正向模式；然而，在深度学习环境中，输入维度通常会大于输出维度。在这种情况下，反向模式更为适用。
在我们的库中，我们将因为这个原因实现反向模式微分。

反向模式微分实现起来稍微有些复杂。

在执行计算时，会构建一个计算图。

例如，下面的图示展示了$f(x)=\frac{2x^2+2y}{4}$的计算图。

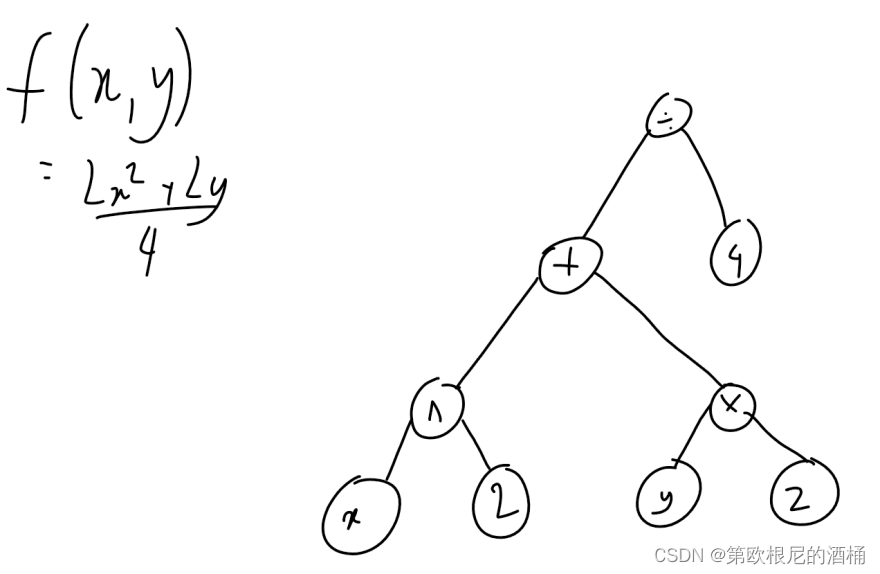
在我们的库中，我们将实现反向模式微分。

反向模式微分在实现上稍微复杂一些。

随着计算执行，将构建出一个计算图。

使用函数评估和图，可以计算出函数中所用所有变量的导数。

这是因为每个操作节点都配备了一种机制，以计算它所涉及的节点的偏导数。

如果我们观察图中的右下角节点（2y的平方节点），乘法节点应该能够计算出相对于"y"节点和"2"节点的导数。

由于导数的计算方法取决于所涉及的操作，因此每个操作节点都会有不同的机制。

当使用图计算导数时，我发现采用深度优先的方式遍历图更为简单。你从最顶部的节点开始，计算它相对于下一个节点的导数（记住，是深度优先遍历），并记录该节点的梯度。然后移动到该节点并重复此过程。每次你在图中下移一级，都将你刚计算的梯度与上一级计算的梯度相乘（这是由于链式法则）。重复这一过程，直到记录了所有节点的梯度。

注意：没有必要计算图中所有的梯度。如果你只想找到单个变量的梯度，一旦计算出它的梯度就可以停止。但是，我们通常希望找出多个变量的梯度，所以一次性计算图中所有的梯度在计算上更为经济，因为它只需要进行一次图求值。如果你只想找出所有你所需的变量的梯度，你将不得不对每个变量进行图的单独求值，这样做在计算上会更加昂贵。

微分规则
这里列出了计算图中每个节点使用的不同微分规则。

注意：所有这些规则都展示了偏导数，这意味着一切非我们正在求梯度的变量都被当作常数对待。

在以下内容中，将 x 和 y 视为图中的节点，而 z 视为这些节点间应用操作的结果。

在乘法节点…

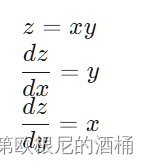
在除法节点处

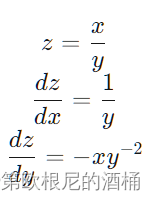
加法：

减法：

幂运算：

链式法则随后用来在图中反向传播所有的梯度…
$$y=f(g(x))\frac{dy}{dx}=f^{\prime }(g(x))\cdot g^{\prime }(x)$$
然而，在进行矩阵乘法时，链式法则会有所不同…
$$z=x\cdot y\frac{dz}{dx}=f^{\prime }(z)\otimes y^T\frac{dz}{dy}=x^T\otimes f^{\prime }(z)$$

代码

第一步：建立Tensor类

import numpy as np
import string
import randomdef id_generator(size=10, chars=string.ascii_uppercase + string.digits):return ''.join(random.choice(chars) for _ in range(size))np.seterr(invalid='ignore')def is_matrix(o):return type(o) == np.ndarraydef same_shape(s1, s2):for a, b in zip(s1, s2):if a != b:return Falsereturn Trueclass Tensor:__array_priority__ = 1000def __init__(self, value, trainable=True):self.value = valueself.dependencies = []self.grads = []self.grad_value = Noneself.shape = 0self.matmul_product = Falseself.gradient = 0self.trainable = trainableself.id = id_generator()if is_matrix(value):self.shape = value.shape

第二步：生成使用随机字符的唯一ID的函数

def id_generator(size=10, chars=string.ascii_uppercase + string.digits):return ''.join(random.choice(chars) for _ in range(size))

第三步：一个简单的函数，检查一个值是否是一个数字数组

def is_matrix(o):return type(o) == np.ndarray

这一行应该是不言自明的，它只是保存了给定张量的值。

self.value = value

如果张量是任何操作的结果，例如加法或除法，这个属性将保存参与该操作产生此张量的张量列表（这就是计算图的构建方式）。如果张量不是任何操作的结果，那么这将是空的。

self.dependencies = [] 
self.grads = []#这个属性将保存每个张量对张量的依赖关系的导数列表。

self.shape 用于存储张量值的形状。只有 numpy 数组有形状，这就是为什么它的默认值是 0。

self.shape = 0
...
if is_matrix(value):self.shape = value.shape

指定张量是否是矩阵乘法的结果（这一点很重要，因为链式法则对矩阵乘法的工作方式有所不同）。

在我们使用计算图来计算梯度之后，这个属性将存储为张量计算出的梯度。它最初被设置为一个和它的值形状相同的全1矩阵。

self.matmul_product = False
self.trainable = trainable
self.id = id_generator()

张量将需要有某种方式来唯一标识自己。当我们在后续的文章中重构我们的优化器以使用这个自动微分模块时，我们将看到这一点的用处。

完整代码

class Tensor:__array_priority__ = 1000def __init__(self, value, trainable=True):self.value = valueself.dependencies = []self.grads = []self.grad_value = Noneself.shape = 0self.matmul_product = Falseself.gradient = 0self.trainable = trainableself.id = id_generator()if is_matrix(value):self.shape = value.shapedef depends_on(self, target):if self == target:return Truedependencies = self.dependenciesfor dependency in dependencies:if dependency == target:return Trueelif dependency.depends_on(target):return Truereturn Falsedef __mul__(self, other):if not (isinstance(other, Tensor)):other = Tensor(other, trainable=False)var = Tensor(self.value * other.value)var.dependencies.append(self)var.dependencies.append(other)var.grads.append(other.value)var.grads.append(self.value)return vardef __rmul__(self, other):if not (isinstance(other, Tensor)):other = Tensor(other, trainable=False)var = Tensor(self.value * other.value)var.dependencies.append(self)var.dependencies.append(other)var.grads.append(other.value)var.grads.append(self.value)return vardef __add__(self, other):if not (isinstance(other, Tensor)):other = Tensor(other, trainable=False)var = Tensor(self.value + other.value)var.dependencies.append(self)var.dependencies.append(other)var.grads.append(np.ones_like(self.value))var.grads.append(np.ones_like(other.value))return vardef __radd__(self, other):if not (isinstance(other, Tensor)):other = Tensor(other, trainable=False)var = Tensor(self.value + other.value)var.dependencies.append(self)var.dependencies.append(other)var.grads.append(np.ones_like(self.value))var.grads.append(np.ones_like(other.value))return vardef __sub__(self, other):if not (isinstance(other, Tensor)):other = Tensor(other)var = Tensor(self.value - other.value)var.dependencies.append(self)var.dependencies.append(other)var.grads.append(np.ones_like(self.value))var.grads.append(-np.ones_like(other.value))return vardef __rsub__(self, other):if not (isinstance(other, Tensor)):other = Tensor(other, trainable=False)var = Tensor(other.value - self.value)var.dependencies.append(other)var.dependencies.append(self)var.grads.append(np.ones_like(other.value))var.grads.append(-np.one_like(self.value))return vardef __pow__(self, other):if not (isinstance(other, Tensor)):other = Tensor(other, trainable=False)var = Tensor(self.value ** other.value)var.dependencies.append(self)var.dependencies.append(other)grad_wrt_self = other.value * self.value ** (other.value - 1)var.grads.append(grad_wrt_self)grad_wrt_other = (self.value ** other.value) * np.log(self.value)var.grads.append(grad_wrt_other)return vardef __rpow__(self, other):if not (isinstance(other, Tensor)):other = Tensor(other, trainable=False)var = Tensor(other.value ** self.value)var.dependencies.append(other)var.dependencies.append(self)grad_wrt_other = self.value * other.value ** (self.value - 1)var.grads.append(grad_wrt_other)grad_wrt_self = (other.value ** self.value) * np.log(other.value)var.grads.append(grad_wrt_self)return vardef __truediv__(self, other):return self * (other ** -1)def __rtruediv__(self, other):return other * (self ** -1)def __matmul__(self, other):if not (isinstance(other, Tensor)):other = Tensor(other, trainable=False)var = Tensor(self.value @ other.value)var.dependencies.append(self)var.dependencies.append(other)var.grads.append(other.value.T)var.grads.append(self.value.T)var.matmul_product = Truereturn vardef __rmatmul__(self, other):if not (isinstance(other, Tensor)):other = Tensor(other, trainable=False)var = Tensor(other.value @ self.value)var.dependencies.append(other)var.dependencies.append(self)var.grads.append(self.value.T)var.grads.append(other.value.T)var.matmul_product = Truereturn var

避免篇幅过长，后面部分在下一篇文章中讲解

这篇关于从零开始学习深度学习库-4：自动微分的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---