立体统计图表绘制方法（饼图）

本文主要是介绍立体统计图表绘制方法（饼图），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

立体统计图表绘制方法（饼图）
记得我学统计学的时候，那些统计图表大都是平面的框框图，很呆板，就只是表现出统计的意义就好了。在网络科技发展进步的当下，原来一些传统的统计图表都有了进一步的创新。在统计图的形式和艺术表现力的美工方面都有了长足的进步。以前企业的PPT都依赖微软的各应用软件来制作图表，现时企业的PPT展示的图表应用不再满足于Excle，Word等的图表绘制方法，进而使用一些第三方应用软件来制作新颖漂亮的图表。由此而有许多图表制作的应用软件面市。这些图表很吸引眼球，我对此也很感兴趣，故试着写了一些各种式样图表的绘制方法，供有同好的同行参考和评论。如果自己在做PPT时加入自己设计制作的图表，我相信这会使人有耳目一新的感觉，还会得到大家的青睐。这会使你感到很有成就感。我就是这样做的。

新样式的统计图有复合式，堆叠式，展开式等等，不一而足。在美工艺术方面有许多独到新颖的样式，给人一个赏心悦目的感受。

今在此提供一种新颖漂亮的立体形式的统计图的绘制方法供参考。

本方法采用C语言的最基本功能：
（ 1）绘图功能画线，画圆，画长方形。
（2）界面美工设计，界面文字打印输出。
代码中有详细的注释，通俗易懂，一看就会。

下面是绘制艺术统计图表的代码：
//变量：可设置成全局变量或私有变量
Canvas cs ; //画布，绘制图表载体
float pi=3.1415926535 ;
float a ; //三角函数 sin (a), cos (a),
float r ; //圆半径 radius
int i, j, n ;
float x0,y0,x1,y1,x2,y2 ; //作图
float dx1,dy1,dx,dy ; //中心坐标
string ss, ss1, ss2,ss3 ; //打印文字
int p[16] ; //set data or input data
int p1[16], p2[16], p3[16] ; //data
double pn ; //显示数据，计算
int ca, cr, cg, cb ; //设置颜色 setColor (a,r,g,b)
int ppn ; //计算
int tb ; //set tab, print
int k0, k1 ; //圆720线起

//*************************
ArtGraphics2 (){ //艺术统计图立体饼图
cs.ClearDraw (0,src); //清屏
clearOutput();
selectStyle () ; //图例样式选项设置
cs.SetFillMode (1);//0不填色，1填色
cs.SetColor (255,250,250,250);
cs.DrawRect (0,4,720,600); //back board
cs.SetColor (255,140,140,140);
cs.DrawRect (24,24,706,586); //back
cs.SetColor (255,220,250,250);
cs.DrawRect (20,20,700,580); //back
cs.SetFillMode (0);//0不填色，1填色
cs.SetColor (255,0,0,250);
cs.DrawRect (20,20,700,580); //back
cs.DrawRect (26,25,694,575); //back

//艺术统计图样例：图例 (立体饼图）
cs.SetFillMode (1);//0不填色，1填色
dx=360; dy=260 ; //center
cs.SetColor (255,250,200,230);
cs.DrawRect (50,80,150,280); //样本值标底
cs.SetStrokeWidth(1); //线
cs.SetTextStyle (0); //1 粗体字
cs.SetTextSize (24);
cs.SetColor(255,0,0,250);
cs.DrawText ("Group ",65,110);
cs.SetTextSize (20);
cs.DrawText (" A",55,140);
cs.DrawText (" B",55,170);
cs.DrawText (" C",55,200);
cs.DrawText (" D",55,230);
cs.DrawText (" E",55,260);

//图例样本值：input data
p1[1]=2760; p1[2]=2400; p1[3]=2880; p1[4]=2040;
p1[5]=1920; //部门 12000
k[0]=180; //k=180,12点钟方向为0位
//k=0, 3点钟方向为0位
k[1]=k[0]+p1[1]*72/1200 ; //样本值合计12000
k[2]=k[1]+p1[2]*72/1200 ; //转换成整圆720线
k[3]=k[2]+p1[3]*72/1200 ;
k[4]=k[3]+p1[4]*72/1200 ;
k[5]=k[4]+p1[5]*72/1200 ;
k[6]=k[5]+p1[6]*72/1200 ;

//绘制饼图，先绘制立体底

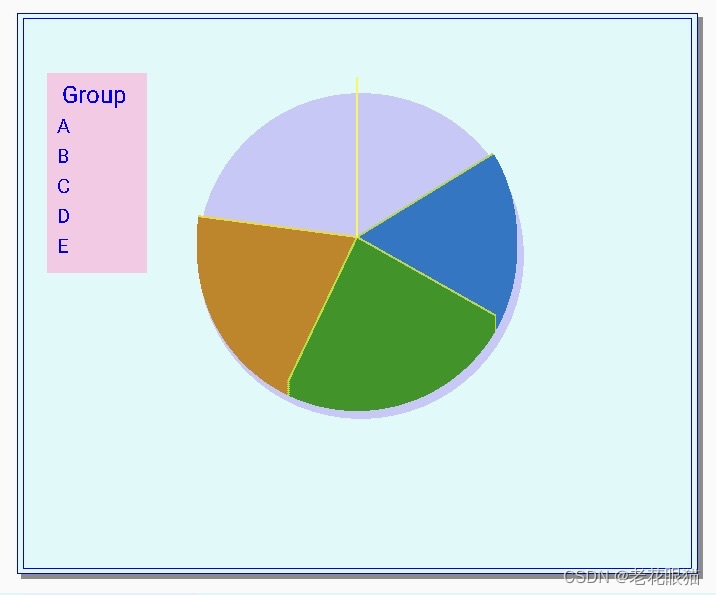
cs.SetStrokeWidth(2); //线宽
dx=360; dy=260 ; r=160 ; //center, radius
cs.SetColor(255,200,200,250);
cs.DrawCircle (dx+4,dy+3, 163) ; //阴影

for (t=1; t<=8 ; t++){ //底16线
dy=dy-2 ;
for (n=2; n<=4 ; n++){ //圆上方少画1和5色块
for (i= k[n-1]; i<=k[n]; i++){
a=pi/360*i ; // a/2 绘出的是半圆
if (n==1) cs.SetColor(255,250,120,200); //设色
if (n==2) cs.SetColor(255,200,130,0);
if (n==3) cs.SetColor(255,0,150,0);
if (n==4) cs.SetColor(255,0,120,200);
if (n==5) cs.SetColor(255,120,50,180);
x0=(float)(r*cos (a))+dx ; //r=radius
y0=(float)(- r*sin (a))+dy ; //逆时针
cs.DrawLine (dx,dy, x0,y0); } } //立体底

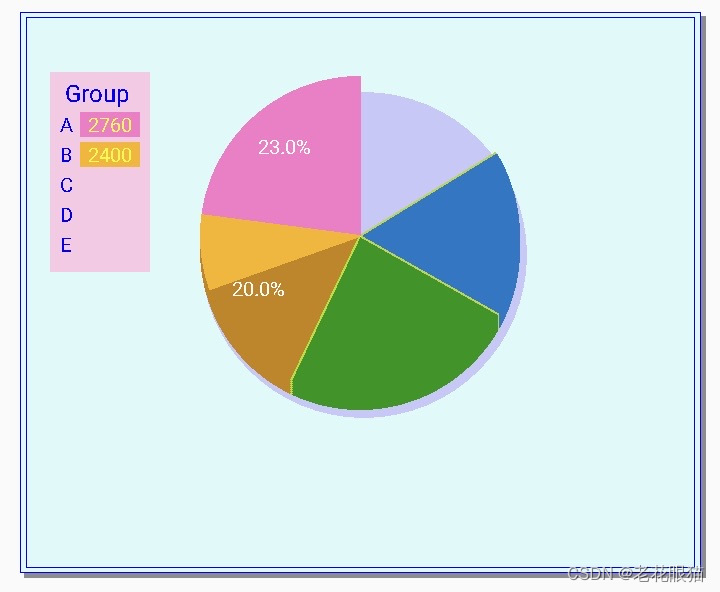
//动画式显示绘制过

//最后绘制面上的饼图 > 完成

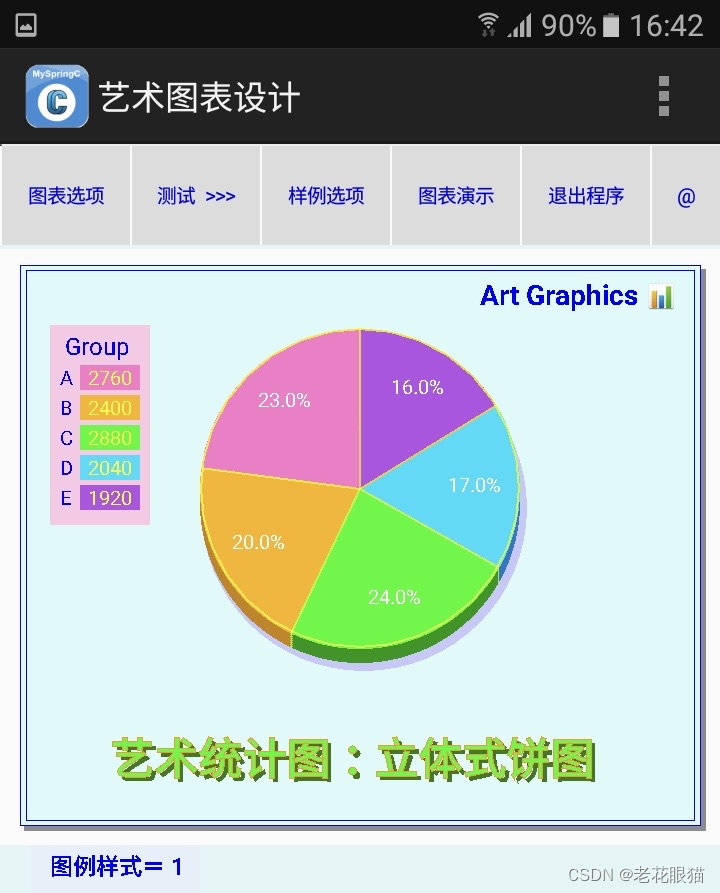
for (n=1; n<=5 ; n++){ //data=5
dy=260-16 ; //完成图上移
for (i= k[n-1]; i<=k[n]+1; i++){
a=pi/360*i ; // a/2 绘出的是半圆
if (n==1) cs.SetColor(255,250,120,200);
if (n==2) cs.SetColor(255,250,180,0);
if (n==3) cs.SetColor(255,0,250,0);
if (n==4) cs.SetColor(255,0,220,250);
if (n==5) cs.SetColor(255,180,80,230);
x0=(float)(r*cos (a))+dx ; //r=radius
y0=(float)(- r*sin (a))+dy ; //逆时针
cs.DrawLine (dx,dy, x0,y0); //绘线
//动画显示逐线绘出加色标
cs.DrawRect (80,n*30+90 ,140,n*30+115); //色标
pn=p1[n]*10 ; //保留1位小数
pn=pn/1200 ;
ss1=doubleToString (pn)+"%" ;
ss2=intToString (p1[n]) ;
cs.SetColor(255,250,250,0);
cs.DrawText(ss2, 88,n*30+110); //标样本值
cs.SetColor(255,250,250,250); //图上标
ma=pi/360*((k[n-1]+k[n])/2) ;
x1=(float)((r-45)*cos (ma))+dx ;
y1=(float)(-(r-45)*sin (ma))+dy ;
cs.DrawText (ss1,x1-27,y1+5); //标%字
cs.Update () ; } }

//show 饼图，动画式显示绘制过程

for (n=0; n<=4 ; n++){
a=pi/360*k[n] ;
x0=(float)(r*cos (a))+dx ; //r=radius
y0=(float)(- r*sin (a))+dy ; //逆时针
cs.SetColor(185,250,250,0);
cs.DrawLine (dx,dy, x0,y0); }//分隔线

cs.SetStrokeWidth(2); //线
cs.SetFillMode (0);//0不填色，1填色
cs.SetColor(205,250,250,0);
cs.DrawCircle (dx,dy-1, 159) ; //加框线

//题标：艺术立体字制作
cs.SetFillMode (1);//0不填色，1填色
cs.SetTextStyle (1);
cs.SetStrokeWidth(1);
cs.SetTextSize (28);
cs.SetColor(255,0,0,250);
cs.DrawText ("Art Graphics 📊",480,60) ;
cs.SetTextSize (46);
ss="艺术统计图：立体式饼图" ;
cs.SetColor(255,50,120,20); //立体字
cs.DrawText (ss,114,534); //阴影
cs.SetColor(255,0,250,0);
cs.DrawText (ss,110,530); //本字
cs.SetFillMode (0);//0不填色，1填色
cs.SetColor(255,250,150,0);
cs.DrawText (ss,110,530); //框线
cs.Update ();
}//ArtGraphics2 ()