本文主要是介绍LeetCode每日一题[C++]-310.最小高度树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目描述
树是一个无向图,其中任何两个顶点只通过一条路径连接。 换句话说,一个任何没有简单环路的连通图都是一棵树。
给你一棵包含 n 个节点的树,标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表(每一个边都是一对标签),其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。
可选择树中任何一个节点作为根。当选择节点 x 作为根节点时,设结果树的高度为 h 。在所有可能的树中,具有最小高度的树(即,min(h))被称为 最小高度树 。
请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。
树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。


解题思路
这道题要统计以每个节点为根的树的最小高度,并返回最小高度的根节点索引。这其实是一类题,可以通过 换根动规 的策略求解。
换根动规
换根动规适用于无向树图枚举每个节点为根的情况。换根动规的基本操作有两步:以某个节点为根先遍历一遍树结构,并记录相应信息;
以同样的节点为根结构再遍历一遍树结构,并在遍历过程中进行换根;
换根动规的基础是这样的:换根是会改变换根的两个节点之间的信息,而其他节点的信息并不变,因此我们可以复用这部分信息以减少暴力遍历每次都遍历所有节点带来的开销。
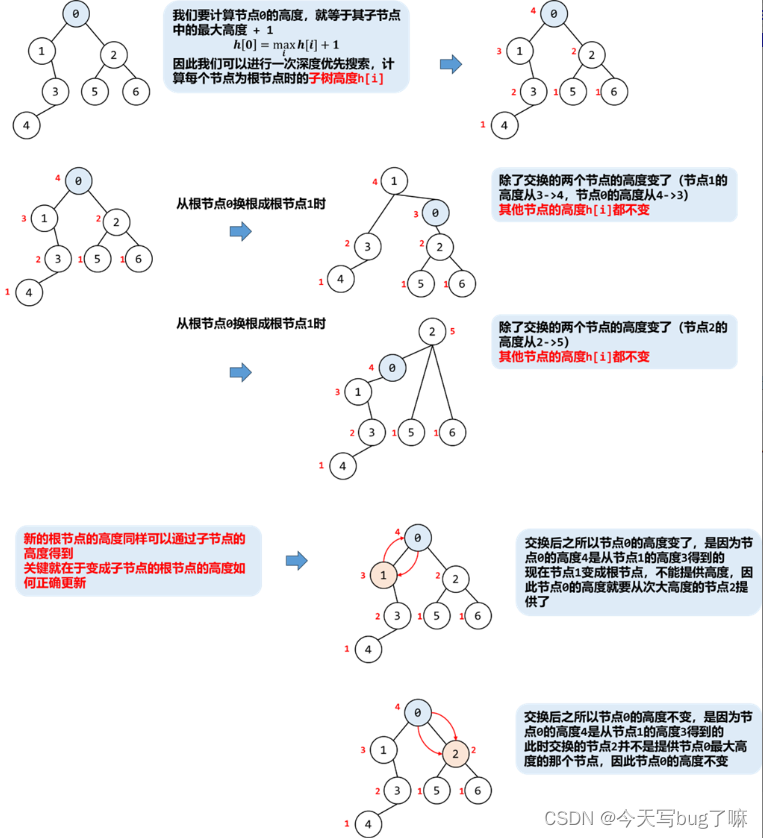
因此:
我们先以节点 0 为根节点进行深度优先搜索,生成初始的每个节点高度 h;
然后再以节点 0 为根节点再次深度优先上搜索,进行换根处理:
设当前根节点为 node,找到其子节点中的最大高度 maxH 和次大高度 secondMaxH,更新根节点的树高度为 rootHeight[node] = maxH + 1;
枚举其此节点进行换根处理,那么 h[node] 就需要进行更新:
如果 h[child] == maxH,即这个子节点就是提供最大高度的子节点。当前根节点变为子节点时,高度发生变化,h[node] = secondMaxH + 1
否则,当前根节点变为子节点时,高度不变, h[node] = maxH + 1;
复杂度分析
时间复杂度:O(n)
空间复杂度:O(n)
代码
class Solution {
private:vector<int> rootHeights; // rootHeights[i]表示以节点i为根的树的高度vector<int> h; // h[i]表示以节点i为根的子树的高度int minHeight; // 最小高度/*** 以节点0为根进行DFS,生成节点node为根的子树的高度*/int dfs_zeroRoot(int node, int pa, vector<vector<int>>& neighbors){int height = 1; // 初始高度为1,表示节点本身for(auto& child: neighbors[node]){if(child == pa)continue; // 跳过父节点height = max(height, dfs_zeroRoot(child, node, neighbors) + 1); // 以节点为根的子树高度 = 所有子节点子树的最大高度 + 1}h[node] = height; // 记录这个值return height;}/*** 换根动规DFS,生成以节点node为根的树的高度*/void dfs_ChangeRoot(int node, int pa, vector<vector<int>>& neighbors){// 统计当前节点node的所有子树的最大高度和次大高度int maxH = 0;int secondMaxH = 0;for(auto& child: neighbors[node]){if(h[child] > maxH){secondMaxH = maxH;maxH = h[child];}else if(h[child] > secondMaxH){secondMaxH = h[child];}}rootHeights[node] = maxH + 1; // 根节点node的高度就等于最大子树高度 + 1minHeight = min(minHeight, rootHeights[node]); // 更新最小高度// 换根,换到子节点为根的树for(auto& child: neighbors[node]){if(child == pa)continue;h[node] = (h[child] == maxH ? secondMaxH : maxH) + 1; // 换根后,当前节点变成子节点的子节点,更新其为根的子树高度dfs_ChangeRoot(child, node, neighbors);}}
public:vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {// 生成邻居节点矩阵vector<vector<int>> neighbors(n);for(auto& e: edges){int x = e[0], y = e[1];neighbors[x].emplace_back(y);neighbors[y].emplace_back(x);}// 生成每个节点为根的子树的高度h.resize(n);dfs_zeroRoot(0, -1, neighbors);// 生成每个节点为根的树的高度rootHeights.resize(n);minHeight = n;dfs_ChangeRoot(0, -1, neighbors); // 找到高度为最小高度的根节点 vector<int> res;for(int i = 0; i < n; i++){if(rootHeights[i] == minHeight)res.emplace_back(i);}return res;}
};这篇关于LeetCode每日一题[C++]-310.最小高度树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






