[海军国际项目办公室]莓良心

本文主要是介绍[海军国际项目办公室]莓良心，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

莓良心

题目概述

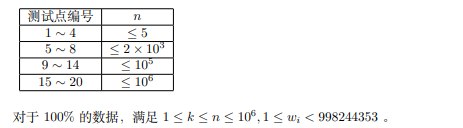
在这里插入图片描述

题解

~~完了，我连NOIP模拟赛的第一题都做不来了。这出题人真的臭呀！！！~~

首先，我们考虑每一份能量会产生怎样的贡献。
无论怎样的划分，它自己都会产生一份贡献，而每当当它与另外的一个数组合起来时，又会产生一份贡献。
所以很容易得到表达式，
$Ans=\sum_{u\in[1,n]}w_{u}{n\brace k}+\sum_{u,v\in[1,n]\,u\not = v}(w_{u}+w_{v}){n\brace k-1}$
前面是 $u$ 单独的贡献，与组合方式无关，后面是两个一起时的贡献，我们就将 $u$ 和 $v$ 绑在一起就行了。
由于不同的 $w_{i}$ 实际上在位置上是等价的，即它们的系数其实是相同的，所以有，
$Ans=\left(\sum_{i=1}^{n}w_{i}\right)\left({n\brace k}+(n-1){n\brace k-1}\right)$
我们只需要算两个斯特林数就行了。
斯特林数显然是可以通过组合加容斥求出的，枚举有多少个集合为空，容斥掉就行了
${n\brace k}=\sum_{i=0}^{k-1}(-1)^i\binom{k}{i}(k-i)^{n}$
$k-i)^n$ 可以用线性筛的方式求出，只算每个质数的次方，其它都乘起来，可以省掉一个 $\ln\,k$ 。

总时间复杂度 $O\left(\frac{n\log\,n}{\ln\,k}+n+k\right)\approx O\left(n\right)$ 。

源码

#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 1000005
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
typedef long long LL;
typedef unsigned long long uLL;       
const int INF=0x3f3f3f3f;       
const int mo=998244353;
const int inv2=499122177;
const int jzm=2333;
const int zero=10000;
const int orG=3,invG=332748118;
const double Pi=acos(-1.0);
const double eps=1e-5;
typedef pair<LL,int> pii;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){_T f=1;x=0;char s=getchar();while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
int gcd(int a,int b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1;}return t;}
int n,k,val[MAXN],fac[MAXN],inv[MAXN],f[MAXN],sum1,sum2,sum;
int ans,prime[MAXN],cntp,pn1[MAXN],pn2[MAXN];bool oula[MAXN];
void init(){fac[0]=fac[1]=inv[0]=inv[1]=f[1]=1;for(int i=2;i<=n;i++)fac[i]=1ll*i*fac[i-1]%mo,f[i]=1ll*(mo-mo/i)*f[mo%i]%mo,inv[i]=1ll*f[i]*inv[i-1]%mo;pn1[0]=pn2[0]=pn1[1]=pn2[1]=1;for(int i=2;i<=n;i++){if(!oula[i])prime[++cntp]=i,pn1[i]=qkpow(i,n,mo),pn2[i]=qkpow(i,n-1,mo);for(int j=1;j<=n&&1ll*i*prime[j]<=n;j++){oula[i*prime[j]]=1;pn1[i*prime[j]]=1ll*pn1[i]*pn1[prime[j]]%mo;pn2[i*prime[j]]=1ll*pn2[i]*pn2[prime[j]]%mo;if(i%prime[j]==0)break;}}
}
int C(int x,int y){if(x<0||y<0||x<y)return 0;return 1ll*fac[x]*inv[y]%mo*inv[x-y]%mo;
}
signed main(){freopen("ichigo.in","r",stdin);freopen("ichigo.out","w",stdout);read(n);read(k);init();for(int i=1;i<=n;i++)read(val[i]),Add(sum,val[i],mo);for(int i=0;i<k;i++){int tmp=(i&1)?mo-C(k,i):C(k,i);Add(sum1,1ll*tmp*pn1[k-i]%mo,mo);Add(sum2,1ll*tmp*pn2[k-i]%mo,mo);}ans=1ll*inv[k]*add(sum1,1ll*(n-1)*sum2%mo,mo)%mo;printf("%d\n",1ll*sum*ans%mo);return 0;
}