第二门课：改善深层神经网络＜超参数调试、正则化及优化＞-超参数调试、Batch正则化和程序框架

本文主要是介绍第二门课：改善深层神经网络＜超参数调试、正则化及优化＞-超参数调试、Batch正则化和程序框架，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1 调试处理

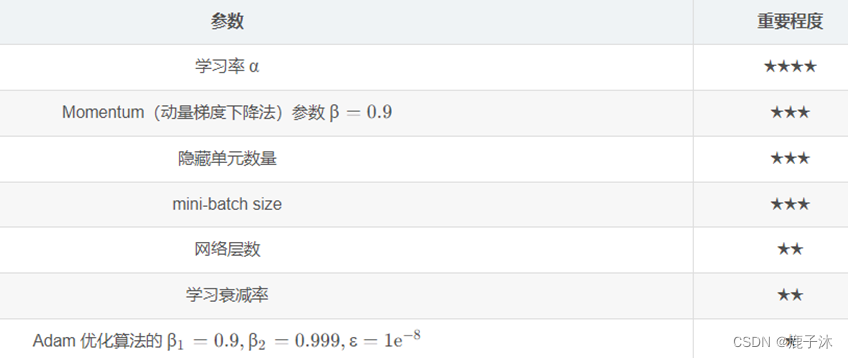
需要调试的参数：α是最重要的。

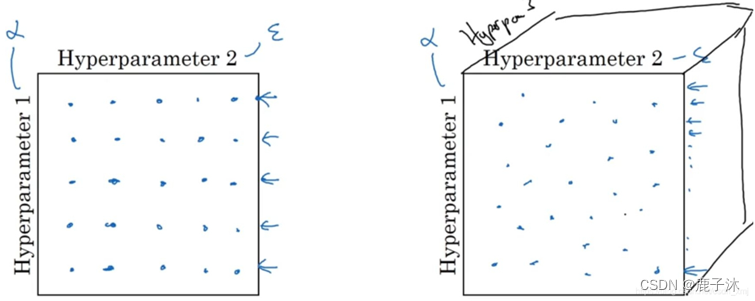
可以采用随机取值，然后选择哪个参数的效果更好。

由粗糙到精细的策略。即放大表现较好的区域(即小篮框内)，然后在其中更密集的取值或随机取值。

2 为超参数选择合适的范围

对于某些超参数（隐藏单元的数量或者神经网络的层数）是可以进行尺度均匀采样的。
某些超参数需要选择不同的合适尺度进行随机采样。随机取值，并不是在范围内均匀取值。
使用对数标尺搜索超参数的方式会更合理
1>比如想取参数 α∈[0.0001,1]
r = -4*np.random.rand()， r∈[−4,0]，然后取 α=10r，在 r 的区间均匀取值
2>再比如计算指数的加权平均值参数 β∈[0.9,0.999]
我们考察 1−β∈[0.001,0.1]，那么我们令r∈[−3,−1]， r 在里面均匀取值， β=1−10r
因为加权平均值大概是基于过去 1\1−β个值进行平均，当 β接近 1 的时候，对细微的变化非常敏感，需要更加密集的取值
当然，如果你使用均匀取值，应用从粗到细的搜索方法，取足够多的数值，最后也会得到不错的结果。

3 超参数调试的实践

在数据更新后，要重新评估超参数是否依然合适
没有计算资源，你可以试验一个或者少量的模型，不断的调试和观察效果（熊猫式）
有计算资源，尽管试验不同参数的模型，最后选择一个最好的（鱼子酱式）

4 归一化网络的激活函数

Batch归一化 会使你的参数搜索问题变得很容易，使神经网络对超参数的选择更加稳定，超参数的范围会更加庞大，工作效果也很好，也会使你的训练更加容易.
对于任意一层的输入 我们将其归一化 z¹

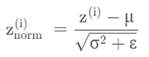
但是我们不想让每一层的均值都为0，方差为1，也许有不同的分布有意义，加上2个超参数 γ,β

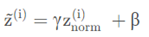
γ和β的作用是使隐藏单元值的均值和方差标准化，即z^(i)有固定的均值和方差，均值和方差可以是0和1，也可以是其它值，它是由γ和β两参数控制的。
当γ=\sqrt{σ^2+ε}, β=μ时，那么z(i)波浪线 = z(i)

5 将Batch Norm拟合进神经网络

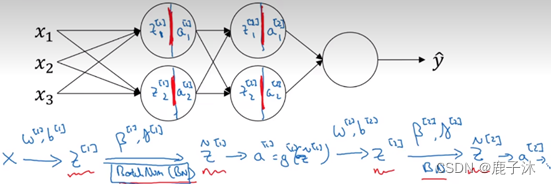
Batch归一化的做法是将z[l]值进行Batch归一化，简称BN，此过程将由β[l]和γ[l]两参数控制，这一操作会给出一个寻得规范化的z[l]值<z[l]波浪线>，然后将其输入激活函数中得到a[l]，即a[l]=gl。
注意：
1>需要强调的是Batch归一化时发生在计算z和a之间的。
2>这里的β,β[1], β[2]和超参数β没有任何关系，Batch归一化中使用β代表此参数(β[1], β[2]等等)，而后者是用于Momentum或计算各个指数的加权平均值。

Mini-batch中与Batch中训练方式相同。

总结用Batch归一化来应用梯度下降法：

6 Batch Norm为什么会奏效？

1 使得输入特征、隐藏单元的值获得类似的范围，可以加速学习。
2 在前面层输入值改变的情况下，BN 使得他们的均值和方差不变（更稳定），即使输入分布改变了一些，它会改变得更少。
它减弱了前层参数的作用与后层参数的作用之间的联系，它使得网络每层都可以自己学习，稍稍独立于其它层，这有助于加速整个网络的学习。
另外，BN 有轻微的正则化效果，因为它在 mini-batch 上计算的均值和方差是有小的噪声，给隐藏单元添加了噪声，迫使后部单元不过分依赖任何一个隐藏单元（类似于 dropout），当增大 mini-batch size ，那么噪声会降低，因此正则化效果减弱。
注：Batch归一化一次只能处理一个mini-batch数据。

7 测试时的Batch Norm

在一个mini-batch中，计算均值和方差，这里用m表示mini-batch中样本数量，而不是整个数据集。注意到μ和σ2是对单个mini-batch中所有m个样本求得的。
用指数加权平均来估算, 这个平均数涵盖了所有 mini-batch (训练过程中计算 μ,σ2 的加权平均)

8 SoftMax回归

SoftMax回归适用于多分类问题

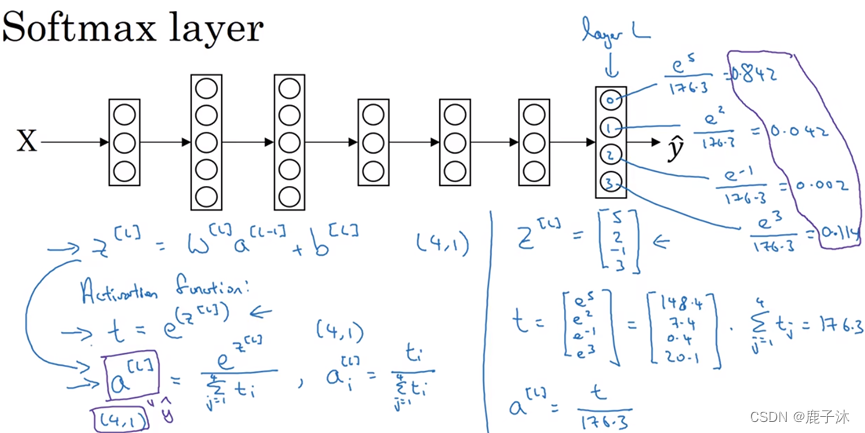
在神经网络最后一层

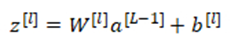
然后计算一个临时变量

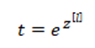
最后将其进行归一化

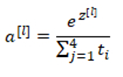
SoftMax激活函数与众不同之处在于需要输入一个4×1维向量，然后输出一个4×1维向量。之前，我们的激活函数都是接受单行数值输入，例如Sigmoid和ReLU激活函数，输入一个实数，输出一个实数。SoftMax激活函数的特殊之处在于，因为需要将所有可能的输出归一化，就需要输入一个向量，最后输出一个向量。
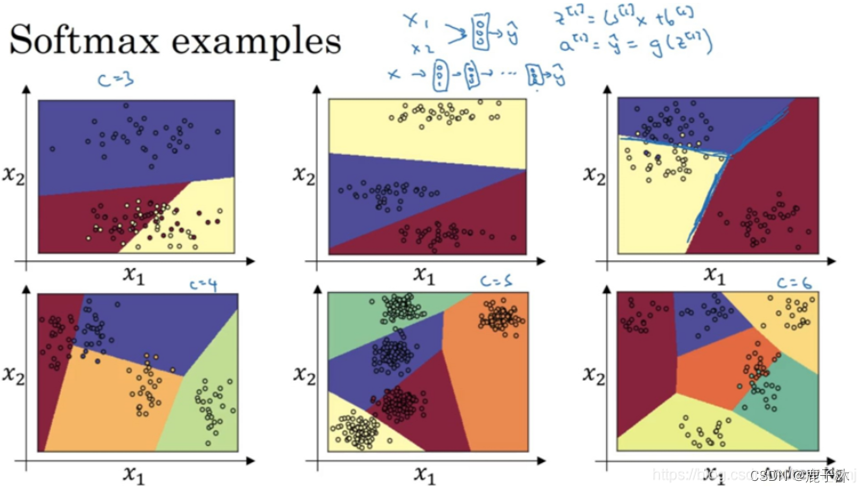
没有隐藏层的神经网络：
输出分类的SoftMax层能够代表这种类型的决策边界，请注意这是几条线性决策边界

9 训练一个SoftMax分类器

SoftMax回归或SoftMax激活函数将logistic激活函数推广到C类，而不仅仅是两类，结果就是如果C=2，那么C=2的SoftMax实际上变回了logistic回归。
训练集中某个样本的真实标签是[0 1 0 0]，上个视频中这表示猫，目标输出y帽=[0.3 0.2 0.1 0.4]，这里只分配20%是猫的概率，所以这个神经网络在本例中表现不佳。
单个函数的训练集损失函数：

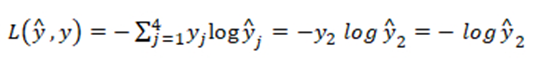
试图将损失函数L变小，因为梯度下降法是用来减少训练集的损失的，要使它变小的唯一方式就是使y2帽尽可能大，即这项输出概率尽可能的大。
整个训练集损失函数：

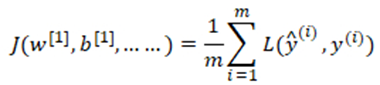
初始化反向传播的关键步骤：

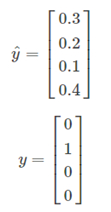
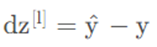
10 深度学习框架

选择框架的标准：
1、便于编程，既包括神经网络的开发和迭代，还包括为产品进行配置
2、运行速度，特别是训练大数据集时，一些框架能让你更高效的运行和训练神经网络。
3、框架是否真的开放，不仅需要开源，而且需要良好的管理。

11 TensorFlow

import numpy as np 
import tensorflow as tf#接下来，让我们定义参数w，在TensorFlow中，你要用tf.Variable()来定义参数 
w = tf.Variable(0,dtype = tf.float32) # 定义损失函数 w**2-10w+25
#cost = tf.add(tf.add(w**2,tf.multiply(- 10.,w)),25) 
#TensorFlow还重载了一般的加减运算等，因此可以表示为以下形式
cost = w**2-10*w+25#让我们用0.01的学习率，目标是最小化损失
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost) #最后下面的几行是惯用表达式: 
init = tf.global_variables_initializer() 
session = tf.Sessions()
#这样就开启了一个TensorFlow session。 
session.run(init)
#来初始化全局变量。 
#然后让TensorFlow评估一个变量，我们要用到: session.run(w) 
#上面的这一行将w初始化为0，并定义损失函数，我们定义train为学习算法，它用梯度下降法优化器使损失函数最小化，但实际上我们还没有运行学习算法，
#所以session.run(w)评估了w，让我们打印结果： 
print(session.run(w))
#所以如果我们运行这个，它评估等于0，因为我们什么都还没运行。#运行一步梯度下降法。
session.run(train)
#让我们评估一下w的值
print(session.run(w)) 
#0.1 
#在一步梯度下降法之后，w现在是0.1。#现在我们运行梯度下降1000次迭代：
for i in range(1000):session.run(train)
print(session.ran(w)) 
#输出结果：4.99999，与5很接近了。

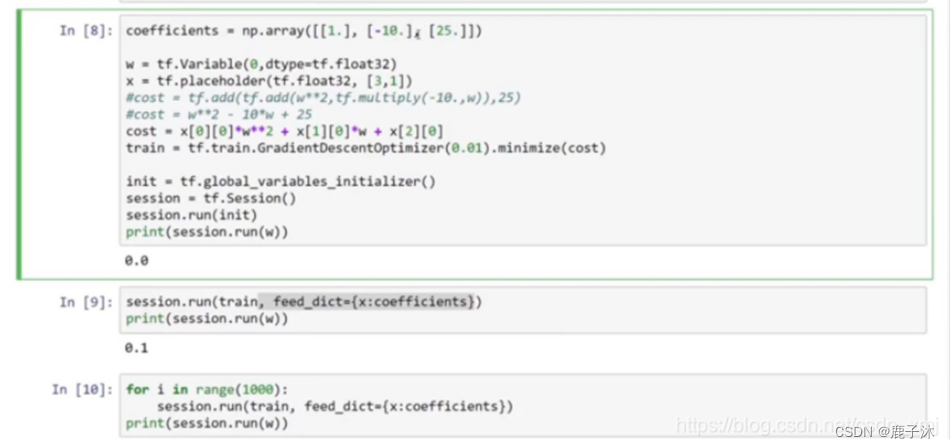
#具体代码讲解：

#让它成为[3,1]数组，因为这个二次方程的三项前有固定的系数，我们可以把这些数字1，-10和25变成数据
x = tf.placeholder(tf.float32,[3,1])
#现在x变成了控制这个二次函数系数的数据，这个placeholder函数告诉TensorFlow，你稍后会为x提供数值。
cost = x[0][0]*w**2 +x[1][0]*w + x[2][0]#让我们再定义一个数组（array），
coefficient = np.array([[1.],[-10.],[25.]])#这就是我们要接入x的数据。最后我们需要用某种方式把这个系数数组接入变量x，做到这一点的句法是，在训练这一步中，要提供给x的数值，在这里设置：
feed_dict = {x:coefficients}

with结构也会在很多TensorFlow程序中用到，它的意思基本上和左边的相同，但是Python中的with命令更方便清理，以防在执行这个内循环时出现错误或例外。

---

1. l ↩︎

这篇关于第二门课：改善深层神经网络＜超参数调试、正则化及优化＞-超参数调试、Batch正则化和程序框架的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---