【leetcode+深度/广度优先搜索】841. 钥匙和房间 (DFS,BFS)

本文主要是介绍【leetcode+深度/广度优先搜索】841. 钥匙和房间 (DFS,BFS)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

leetcode-cn：leetcode面试75道精华：https://leetcode.cn/studyplan/leetcode-75/
841.钥匙和房间：https://leetcode.cn/problems/keys-and-rooms/description/

一、题目：841. 钥匙和房间

有 n 个房间，房间按从 0 到 n - 1 编号。最初，除 0号房间外的其余所有房间都被锁住。 你的目标是进入所有的房间。然而，你不能在没有获得钥匙的时候进入锁住的房间。

当你进入一个房间，你可能会在里面找到一套不同的钥匙，每把钥匙上都有对应的房间号，即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。

给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入 所有 房间返回 true，否则返回

示例

示例 1： 输入：rooms = [[1],[2],[3],[]] 输出：true 解释： 我们从 0 号房间开始，拿到钥匙 1。
之后我们去 1 号房间，拿到钥匙 2。 然后我们去 2 号房间，拿到钥匙 3。 最后我们去了 3 号房间。
由于我们能够进入每个房间，我们返回 true。

示例 2： 输入：rooms = [[1,3],[3,0,1],[2],[0]] 输出：false 解释：我们不能进入 2 号房间。

提示：

n == rooms.length
2 <= n <= 1000
0 <= rooms[i].length <= 1000
1 <=sum(rooms[i].length) <= 3000
0 <= rooms[i][j] < n
所有 rooms[i] 的值 互不相同

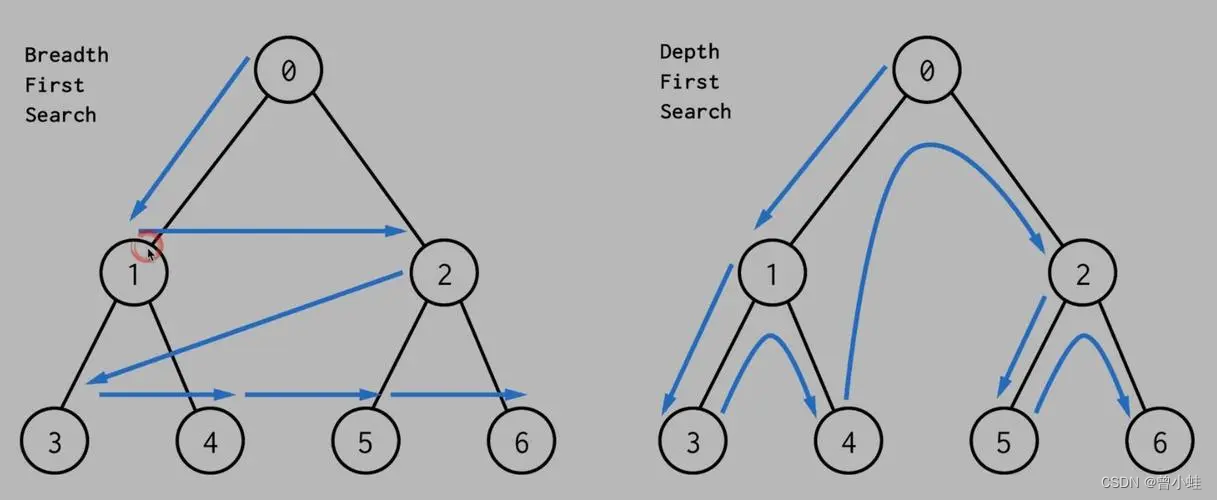
解法1：深度优先搜索 （DFS, Depth First Search）

深度优先搜索（DFS）（算法笔记）：https://blog.csdn.net/Arabot_/article/details/129702049

深度优先搜索属于搜索问题的一种，当问题可以被描述为“路径搜索”时，就可以采用搜素问题的所有解的方式来进行解决，所以DFS本质还是暴力。

深度搜索具有两个关键词，即“岔道口”和“死胡同”，这两个词来源于迷宫问题，这也是搜索问题最原始的表现。
当碰到岔道口时（一次多个选择时），总是以“深度”作为前进的关键词，不碰到死胡同就不回头，因此被称为“深搜”。
深搜适合于求解需要**遍历所有解或路径的问题**，并且剪枝很重要。
深搜和广搜在数据结构中的应用就是对非线性存储结构进行遍历。
搜索和分治是两大分析问题的方法，而回溯、剪枝、动态规划可以说是对深度搜索和分治算法进行优化。

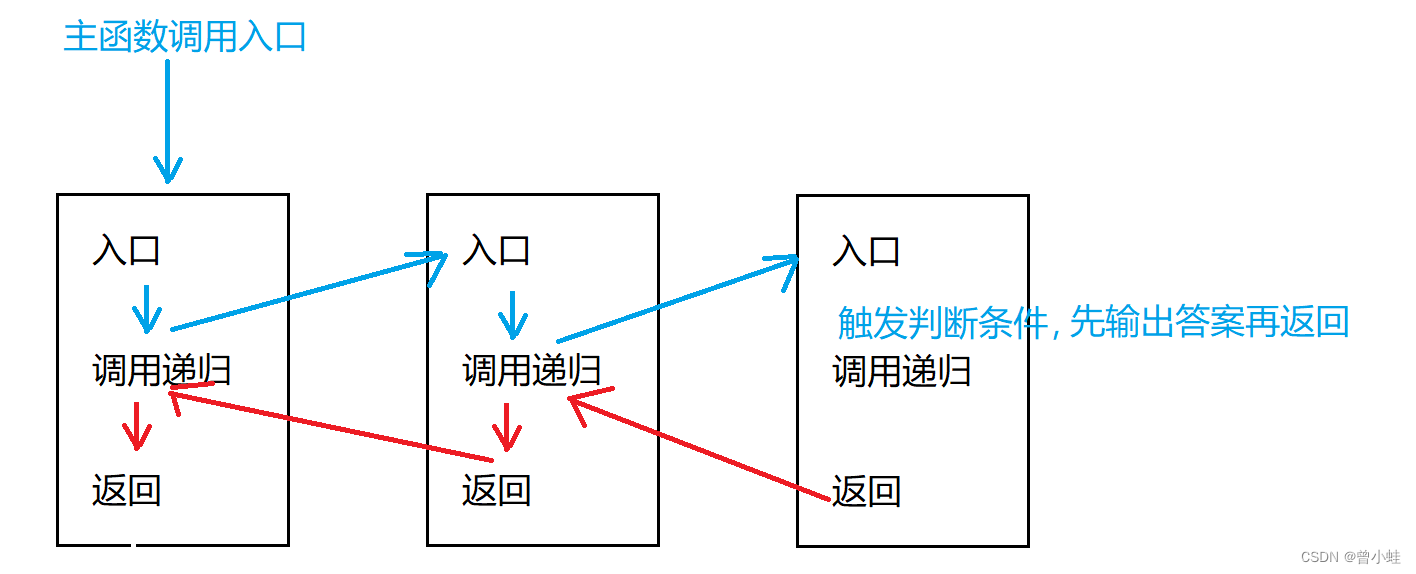
思路 （常用递归）

from https://leetcode.cn/problems/keys-and-rooms/solutions/18826/7xing-dfs-8xing-bfs-liang-chong-fang-fa-san-chong-

1. 先找第 ０ 个房间的第一个钥匙
2. 进入那个房间，再找它的第一个钥匙 重复以往，直到没钥匙了，
3. 那么退回当前房间 ，找到房间的第二把钥匙，如果该房间没有，则返回上一间房间 ，重复以往

递归调用函数的

python代码

class Solution:def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:# 抽象# 一个数字就是一个房间，以及二维数组中数据，也可以通用理解为节点序号# set add remove 添加删除原始# set1.union(set2)   并集# set1.intersection(set2) 交集# 如果没有返回，程序自动返回继续执行# nonlocal 关键字用于在嵌套函数中声明一个变量不属于本地作用域，# 它指向的是上一层函数的局部变量。这意味着你可以在嵌套函数中修改外部函数的变量。def dps(x):vist.add(x)for key in rooms[x]:if key not in vist:dps(key)vist=set()dps(0)num_rooms=len(rooms)return  len(vist)==num_rooms

python多级嵌套函数如何理解？

嵌套函数可以访问其外部函数的变量和参数，这是一种封装和组织代码的方式

 def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:def dfs(x: int):vist.add(x)vist=set()

python set 和list 数据结构有什么区别?

vist=set()
# 或 vist={0}

Python 中的 set 和 list 是两种不同的数据结构，它们在元素操作方面有一些显著的区别：

1. 元素唯一性：
   set：集合中的元素是唯一的，不允许重复。
   list：列表中的元素可以重复，没有唯一性要求。

2. 元素顺序：
   set：集合中的元素是无序的，不能通过索引访问元素。
   list：列表中的元素是有序的，可以通过索引访问和操作元素。

3. 性能：
   set：由于集合使用哈希表实现，因此在查找、添加和删除元素时通常具有较高的性能。
   list：列表的查找和删除操作（特别是对于大量元素）可能比集合慢，因为它们需要遍历整个列表。

4. 元素操作：
   set：
   添加元素：使用 add() 方法。
   删除元素：使用 remove()（如果元素不存在会引发错误）或 discard()（如果元素不存在也不会引发错误）方法。
   交集、并集、差集等操作：使用 intersection(), union(), difference() 等方法。

list：
添加元素：使用 append() 方法或 insert() 方法。
删除元素：使用 remove() 方法（删除第一个匹配的元素）或 pop() 方法（删除指定索引处的元素）。
排序、反转等操作：使用 sort(), reverse() 等方法。

解法2 ： 广度优先搜索 （BFS）

https://leetcode.cn/problems/keys-and-rooms/solutions/18826/7xing-dfs-8xing-bfs-liang-chong-fang-fa-san-chong-

1. 首先，建立一个登记表（python中用双向队列或者list实现），把 ０ 号房间的所有钥匙都依次记录，
2. 然后删除0号房间在登记表（队列）记录，同时用一个visited表（set）记录已经去过的房间，防止重复登记
3. 进入队列记录表中最早登记的房间（X号房间），结合（visited表）进行登记，去过的就不登记到队列记录表，登记完钥匙后，删除x号房间的记录
4. 继续按按队列登记表的房间进入查找、登记，直到队列登记表没有要去的房间，表示所有能打开的房间都检查完了，
5. 最后根据（visited表）房间的数量与已知房间数量对比，得出能否打开所有的房间（len(visited)==len(rooms)）

BFS的python代码

其中 collections.deque() # 创建一个空队列，这个是双向的队列

class Solution:def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:queue=collections.deque()  # 创建一个空队列，这个是双向的队列# 先将第0号房间添加到检查列表queue.extend(rooms[0])visited={0}  # 已经去过的房间while(len(queue)!=0):search_room_id=queue.pop() #  移除并返回队列的右端元素visited.add(search_room_id)for key in rooms[search_room_id]:if key not in visited:  # 获得钥匙是否去过，非常重要，否则会反复去queue.append(key)print(visited,num_room)return  len(visited)==len(rooms)

python双向队列deque的操作方法

append(x)    在队列的**右端**添加一个元素。
appendleft(x)  在队列的**左端**添加一个元素。extend(iterable) 在队列的右端添加多个元素，其中 iterable 可以是列表、集合或任何迭代器。
extendleft(iterable)，在队列的左端添加多个元素，iterable 中的元素会被逆序添加到队列中。pop()   **移除并返回**队列的右端元素。
popleft()  移除并返回队列的左端元素。
remove(value)  移除队列中第一个匹配的 value 元素
clear()移除队列中的所有元素。count(x)计算队列中元素 x 出现的次数。
reverse()  将队列中的元素反转。
copy()  创建并返回队列的一个浅拷贝。index(x, start=0, stop=sys.maxsize)返回找到的第一个 x 元素的索引，索引范围从 start 到 stop。
insert(i, x)  在队列的指定位置 i 插入元素 x。如果插入会导致 deque 超过 maxlen 的限制，则会引发 IndexError。

具体操作

# 使用 extendleft 方法在队列头部添加列表中的所有元素
queue.extendleft(list_elements)print("队列的内容:", list(queue))

二、 巩固：547. 省份数量 (分类)

https://leetcode.cn/problems/number-of-provinces/description/?envType=study-plan-v2&envId=leetcode-75
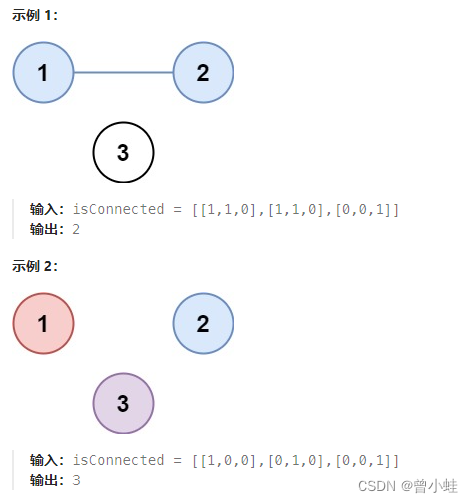
有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量

算法-深度优先

思路：
对于每个城市，如果该城市尚未被访问过，则从该城市开始深度优先搜索，通过矩阵 isConnected 得到与该城市直接相连的城市有哪些，这些城市和该城市属于同一个连通分量，然后对这些城市继续深度优先搜索，直到同一个连通分量的所有城市都被访问到，即可得到一个省份。
遍历完全部城市以后，即可得到连通分量的总数，即省份的总数。

链接：https://leetcode.cn/problems/number-of-provinces/solutions/549895/sheng-fen-shu-liang-by-leetcode-solution-eyk0/

class Solution:def findCircleNum(self, isConnected: List[List[int]]) -> int:visited=set()def dfs(city_id):visited.add(city_id)for j in range(0,len(isConnected)):if j not in visited and  isConnected[city_id][j] == 1:dfs(j)count=0# 每次迭代，就把把一个省的城市找完for i in range(len(isConnected)):# 检查过的城市不用去了if  i not in visited:count+=1dfs(i)return count

其他题 （DPS/ BPS）

.1466. 重新规划路线
. 994 发烂的橘子 ：https://leetcode.cn/problems/rotting-oranges

附录

原题

这篇关于【leetcode+深度/广度优先搜索】841. 钥匙和房间 (DFS,BFS)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---