本文主要是介绍图文证明 洛必达法则,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
洛必达法则
- 洛必达法则
- 引入切线
- 构建关键函数
- 证明 为什么洛必达法则对于 0 0 \frac{0}{0} 00型生效?
- 证明 为什么洛必达法则对于 ∞ ∞ \frac{\infty}{\infty} ∞∞型生效?
- 洛必达法则对于别的类型是否生效?
- 参考文章
洛必达法则
洛必达法则:
如果在极限计算中遇到 0 0 \frac{0}{0} 00或 ∞ ∞ \frac{\infty}{\infty} ∞∞的形式,可以使用该法则进行简化。
lim x → a f ( x ) g ( x ) = lim x → a f ′ ( x ) g ′ ( x ) \lim_{{x \to a}} \frac{f(x)}{g(x)} = \lim_{{x \to a}} \frac{f'(x)}{g'(x)} x→alimg(x)f(x)=x→alimg′(x)f′(x)
其中, f ′ ( x ) f'(x) f′(x)和 g ′ ( x ) g'(x) g′(x)分别表示 f ( x ) f(x) f(x)和 g ( x ) g(x) g(x)的导数。
可见,洛必达法则的核心功能就是,大大简化了极限运算。
- 为什么洛必达法则对于 0 0 \frac{0}{0} 00型和 ∞ ∞ \frac{\infty}{\infty} ∞∞型
生效? - 洛必达法则对于别的类型是否生效?
引入切线
斜率的概念;
a 点的斜率可以表示为:
lim x → a f ( x ) − f ( a ) x − a \lim_{{x \to a}} \frac{f(x)-f(a)}{x-a} x→alimx−af(x)−f(a)

由图可以看出,B靠近a点时候的变化
割线的极限即是切线
构建关键函数
令函数: u ( x ) = u ( g ( x ) , f ( x ) ) u(x)=u(g(x),f(x)) u(x)=u(g(x),f(x))
根据切线的表示方法g(x) 为 x,f(x) 为 y,可以得a处的斜率为:
u ′ ( a ) = f ( x ) − f ( a ) g ( x ) − g ( a ) u'(a) = \frac{f(x)-f(a)}{g(x)-g(a)} u′(a)=g(x)−g(a)f(x)−f(a)
对上下同时除 x-a:
u ′ ( a ) = f ( x ) − f ( a ) x − a ⋅ x − a g ( x ) − g ( a ) u'(a) = \frac{f(x)-f(a)}{x-a} \cdot \frac{x-a}{g(x)-g(a)} u′(a)=x−af(x)−f(a)⋅g(x)−g(a)x−a
我们将前后分开看,还是根据斜率表达式可得:
u ′ ( a ) = f ′ ( a ) ⋅ 1 g ′ ( a ) u'(a)=f'(a) \cdot \frac{1}{g'(a)} u′(a)=f′(a)⋅g′(a)1
所以得出一点的斜率为:
u ′ ( x ) = f ′ ( x ) g ′ ( x ) u'(x)= \frac{f'(x)}{g'(x)} u′(x)=g′(x)f′(x)
对于函数u(x)上任意一点和原点的连线 l l l 的斜率:
l ′ ( x ) = f ( x ) g ( x ) l'(x)= \frac{f(x)}{g(x)} l′(x)=g(x)f(x)
我们要证明这个:
lim x → a f ( x ) g ( x ) = lim x → a f ′ ( x ) g ′ ( x ) \lim_{{x \to a}} \frac{f(x)}{g(x)} = \lim_{{x \to a}} \frac{f'(x)}{g'(x)} x→alimg(x)f(x)=x→alimg′(x)f′(x)
现在已经有了 f ( x ) g ( x ) \frac{f(x)}{g(x)} g(x)f(x) 和 f ′ ( x ) g ′ ( x ) \frac{f'(x)}{g'(x)} g′(x)f′(x)的两个式子了
证明 为什么洛必达法则对于 0 0 \frac{0}{0} 00型生效?
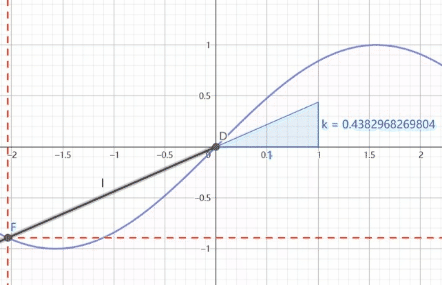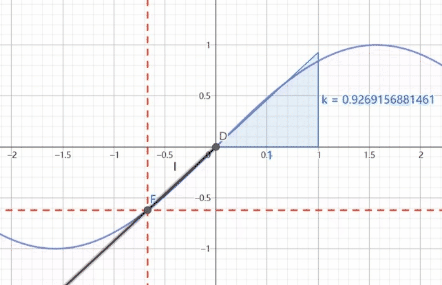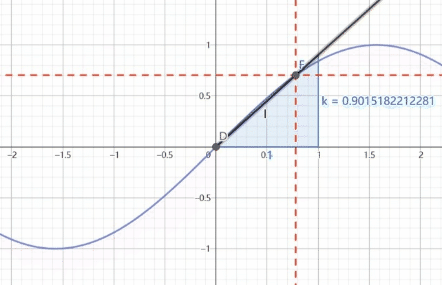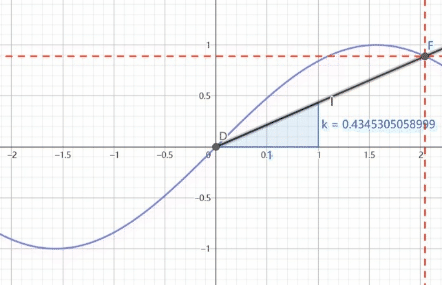
f ( x ) g ( x ) \frac{f(x)}{g(x)} g(x)f(x)是原点线的斜率
f ′ ( x ) g ′ ( x ) \frac{f'(x)}{g'(x)} g′(x)f′(x)是某点处的斜率
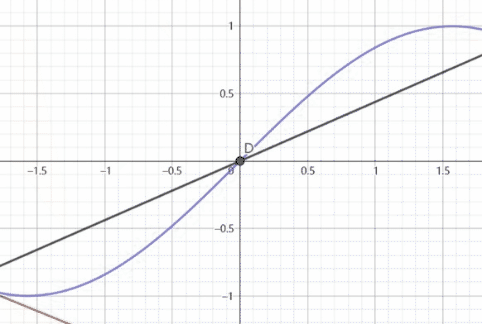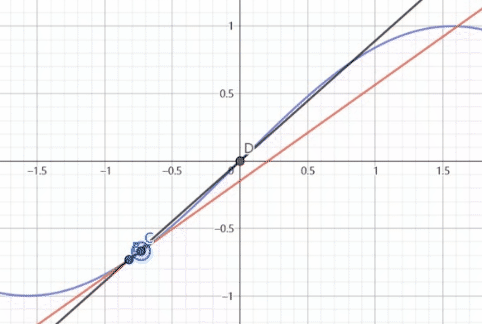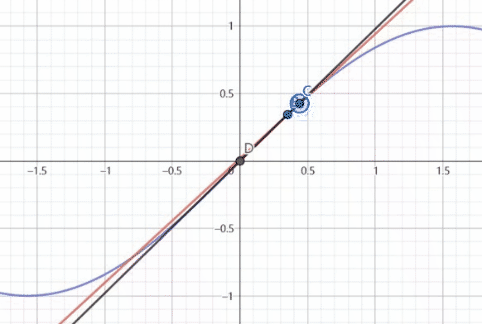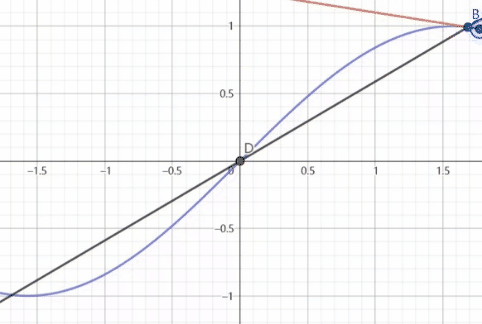
B,C两点是来确定切线的就如同上面引入的切线公式一样
B,C两点确定的切线就是 f ′ ( x ) g ′ ( x ) \frac{f'(x)}{g'(x)} g′(x)f′(x)是某点处的斜率
黑色的函数是 f ( x ) g ( x ) \frac{f(x)}{g(x)} g(x)f(x)是原点线的斜率
根据这个动图我们可以看出,在过原点的时候,两条线直接重合,而接近原点时其实就是f(x),g(x)趋近0时
所以有当上下都趋于0时有:
0 0 \frac{0}{0} 00的形式,可以使用该法则进行简化。
lim x → a f ( x ) g ( x ) = lim x → a f ′ ( x ) g ′ ( x ) \lim_{{x \to a}} \frac{f(x)}{g(x)} = \lim_{{x \to a}} \frac{f'(x)}{g'(x)} x→alimg(x)f(x)=x→alimg′(x)f′(x)
证明 为什么洛必达法则对于 ∞ ∞ \frac{\infty}{\infty} ∞∞型生效?
在欧式几何中,两条线的斜率要相等,只有两种情况,重合或者平行。
这就是 ∞ ∞ \frac{\infty}{\infty} ∞∞型为什么适用于洛必达法则的原因,我们来一起推导一下。
前面证明 0 0 \frac{0}{0} 00型,就是因为趋向于0时发生了重合斜率相等

而 ∞ ∞ \frac{\infty}{\infty} ∞∞型要证明洛必达,也要证明趋向于 ∞ {\infty} ∞时两条线的斜率要相等
首先有一个有趋向于 ∞ {\infty} ∞的函数 x 2 x^2 x2
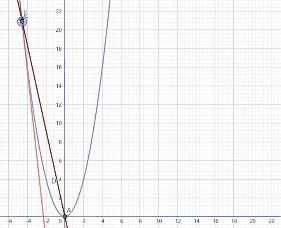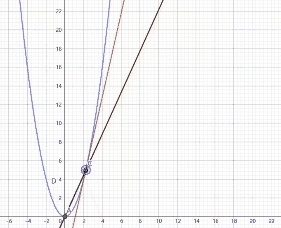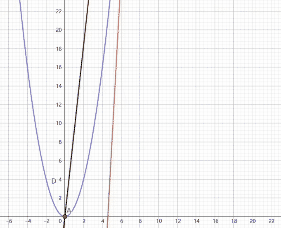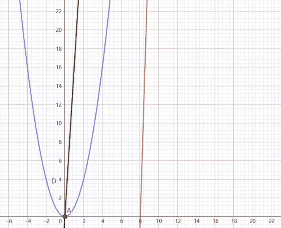
和 0 0 \frac{0}{0} 00型一样的图像证明
B,C两点是来确定切线的就如同上面引入的切线公式一样
B,C两点确定的切线就是 f ′ ( x ) g ′ ( x ) \frac{f'(x)}{g'(x)} g′(x)f′(x)是某点处的斜率
黑色的函数是 f ( x ) g ( x ) \frac{f(x)}{g(x)} g(x)f(x)是原点线的斜率
根据这个动图我们可以看出,在趋向于 ∞ {\infty} ∞的时候,两条线平行,而接近 ∞ {\infty} ∞时其实就是f(x),g(x)趋近 ∞ {\infty} ∞时
所以有当上下都趋于 ∞ {\infty} ∞时有:
∞ ∞ \frac{{\infty}}{{\infty}} ∞∞的形式,可以使用该法则进行简化。
lim x → a f ( x ) g ( x ) = lim x → a f ′ ( x ) g ′ ( x ) \lim_{{x \to a}} \frac{f(x)}{g(x)} = \lim_{{x \to a}} \frac{f'(x)}{g'(x)} x→alimg(x)f(x)=x→alimg′(x)f′(x)
洛必达法则对于别的类型是否生效?
根据上面的证明过程可以发现
只要原点线和割线斜率相等,就可以运用洛必达法则
参考文章
【洛必达法则】的动画证明+深入理解
这篇关于图文证明 洛必达法则的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









