树剖树剖　洛谷　P3384 【模板】轻重链剖分 (我爱树剖)

　　　写了半天的树剖，终于调出来了，起始当你掌握了tarjan(时间戳和dfs序)和线段树之后，理解树剖还是不难的，就是实现起来挺麻烦的。树剖可以ｎlogn的解决树上ＬＣＡ（动态的的也可以），它可以loglogn(利用线段树)处理出树上两个节点路径上的修改。

　　第一次操作实现子树的大小和重儿子是谁，然后第二次dfs求出对应下标和对应的根节点，顺便记录线段树的初始值。

void dfs1(ll now,ll f)
{ll k=0;fa[now]=f;size[now]=1;deep[now]=deep[f]+1;for(ll i=head[now];~i;i=A[i].next){if(A[i].to!=f){dfs1(A[i].to,now);size[now]+=size[A[i].to];if(size[A[i].to]>k){k=size[A[i].to];son[now]=A[i].to;}}}return ;
}void dfs2(ll now,ll f)
{top[now]=f;id[now]=++num;wt[id[now]] = a[now];if(son[now]==0) return ; // 没有儿子了dfs2(son[now],f);for(ll i=head[now];~i;i=A[i].next){if(A[i].to!=fa[now]&&A[i].to!=son[now]){dfs2(A[i].to,A[i].to);}}
}

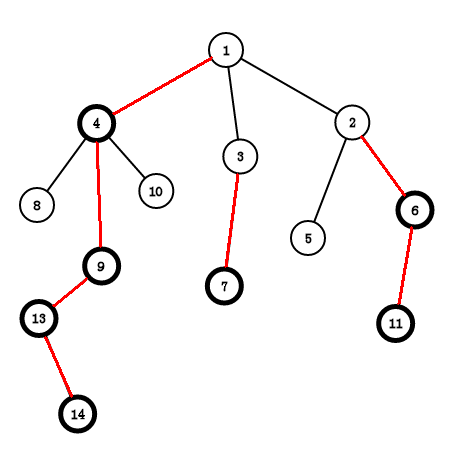
　　红色边的点集合就是我们预处理出的链，考虑到每条链的性质，一定从轻节点开始一路走重儿子，然后我们给每一条剖出来的链打上下标，利用线段树实现区间修改即可。

喜闻乐见直接上模板，懒得写了ｈｈｈ

//#pragma GCC optimize(3)
#include <bits/stdc++.h>
#define debug(x) cout<<#x<<":"<<x<<endl;
//#define _CRT_SECURE_NO_WARNINGS
typedef  long long ll;
using namespace std;
#define rep(i,j,n) for(ll i=j;i<=n;i++)
#define per(i,j,n) for(ll i=j;i>=n;i--)
typedef unsigned long long ull;
typedef unsigned short us;
const ll INF= 1e18+7;
const ll maxx = 2e5+700;
ll mod;
const double eps=1e-8;
inline bool read(ll &num){char in;bool IsN=false;in=getchar();if(in==EOF) return false;while(in!='-'&&(in<'0'||in>'9')) in=getchar();if(in=='-'){ IsN=true;num=0;}else num=in-'0';while(in=getchar(),in>='0'&&in<='9'){num*=10,num+=in-'0';}if(IsN) num=-num;return true;}
ll n,m;
ll fa[maxx],deep[maxx],size[maxx],son[maxx];
ll wt[maxx];
/// 转换下标后对应的值
/// fa[i]:i的父亲节点  son[i]:i的重儿子struct stu
{ll to,next;
}A[maxx*2];
ll head[maxx],cnt=0;
ll tree[maxx*4],lazy[maxx*4];
ll top[maxx],id[maxx],a[maxx];ll num=0;
void add(ll u,ll v)
{A[cnt].to=v;A[cnt].next=head[u];head[u]=cnt++;
}void dfs1(ll now,ll f)
{ll k=0;fa[now]=f;size[now]=1;deep[now]=deep[f]+1;for(ll i=head[now];~i;i=A[i].next){if(A[i].to!=f){dfs1(A[i].to,now);size[now]+=size[A[i].to];if(size[A[i].to]>k){k=size[A[i].to];son[now]=A[i].to;}}}return ;
}void dfs2(ll now,ll f)
{top[now]=f;id[now]=++num;wt[id[now]] = a[now];if(son[now]==0) return ; // 没有儿子了dfs2(son[now],f);for(ll i=head[now];~i;i=A[i].next){if(A[i].to!=fa[now]&&A[i].to!=son[now]){dfs2(A[i].to,A[i].to);}}
}void pushup(ll x)
{tree[x]=(tree[x<<1]+tree[x<<1|1])%mod;
}void build(ll x,ll l,ll r)
{if(l==r){tree[x]=wt[l]%mod;return ;}ll mid=(l+r)>>1;build(x<<1,l,mid);build(x<<1|1,mid+1,r);pushup(x);
}
void down(ll x,ll l,ll r)
{if(lazy[x]==0) return ;ll mid=(l+r)>>1;lazy[x<<1]=(lazy[x<<1]+lazy[x])%mod;lazy[x<<1|1]=(lazy[x<<1|1]+lazy[x])%mod;tree[x<<1]=(tree[x<<1]+ lazy[x]*(mid-l+1) ) %mod;tree[x<<1|1]=(tree[x<<1|1]+ lazy[x]*(r-mid) ) %mod;lazy[x]=0;return ;
}
void modify(ll x,ll l,ll r,ll ql,ll qr,ll val)
{if(ql<=l&&qr>=r){tree[x]=(tree[x] + val*(r-l+1) ) %mod;lazy[x]=(lazy[x] +val)%mod;return ;}down(x,l,r);ll mid=(l+r)>>1;if(ql<=mid) modify(x<<1,l,mid,ql,qr,val);if(qr>mid) modify(x<<1|1,mid+1,r,ql,qr,val);pushup(x);
}
ll ask(ll x,ll l,ll r,ll ql,ll qr)
{if(ql<=l&&qr>=r){return tree[x];}down(x,l,r);ll ans=0;ll mid=(l+r)>>1;if(ql<=mid)ans=( ans+ask(x<<1,l,mid,ql,qr))%mod;if(qr>mid) ans= ( ans+ ask(x<<1|1,mid+1,r,ql,qr))%mod;return ans%mod;
}
void addpath(ll x,ll y,ll k)
{while(top[x]!=top[y])// 当前不在一条链上，往同一条练上走{// 让ｘ深if(deep[top[x]]<deep[top[y]])swap(x,y);//printf("那 dwqdwq %lld -- %lld\n",id[top[x]],id[x]);modify(1,1,n,id[top[x]],id[x],k);x=fa[top[x]];}if(deep[x]>deep[y]) swap(x,y);//printf("那 dwqdwq %lld -- %lld\n",id[x],id[y]);modify(1,1,n,id[x],id[y],k);
}ll query(ll x,ll y)
{ll ans=0;while(top[x]!=top[y])// 当前不在一条链上，往同一条练上走{// 让ｘ深if(deep[top[x]]<deep[top[y]])swap(x,y);ans= ( ans+ ask(1,1,n,id[top[x]],id[x]))%mod;x=fa[top[x]];}if(deep[x]>deep[y]) swap(x,y);ans=(ans+ask(1,1,n,id[x],id[y]))%mod ;return ans%mod;
}ll addson(ll x,ll k)
{modify(1,1,n,id[x],id[x]+size[x]-1,k);
}
ll queryson(ll x)
{// printf("%lld  %lld\n",id[x],id[x]+size[x]-1);return ask(1,1,n,id[x],id[x]+size[x]-1)%mod;
}
int main()
{ll t;ll ans=0;ll r;rep(i,1,maxx-1) head[i]=-1;cin>>n>>m>>r>>mod;//rep(i,1,n) scanf("%lld",&a[i]);rep(i,1,n-1){ll x,y;scanf("%lld%lld",&x,&y);add(x,y);add(y,x);}dfs1(r,0);dfs2(r,r);build(1,1,n);/*rep(i,1,n){printf("%lld的重儿子和子树大小 :%lld %lld\n",i,son[i],size[i]);}rep(i,1,n){printf("%lld属于的链和对应的ｉｄ :%lld %lld\n",i,top[i],id[i]);}*/rep(i,1,m){ll id,x,y,z;scanf("%lld",&id);if(id==1){scanf("%lld%lld%lld",&x,&y,&z);addpath(x,y,z);}else if(id==2){scanf("%lld%lld",&x,&y);//printf("dezhi : %lld\n",ask(1,1,n,2,2));printf("%lld\n",query(x,y));}else if(id==3){scanf("%lld%lld",&x,&y);addson(x,y);}else{scanf("%lld",&x);printf("%lld\n",queryson(x));}}return 0;
}
/*
8 10 2 448348
458 718 447 857 633 264 238 944
1 2
2 3
3 4
6 2
1 5
5 7
8 6
3 7 611
4 6
3 1 267
3 2 111
1 6 3 153
3 7 673
4 8
2 6 1
4 7
3 4 2281208
1055
2346
1900*/