Python 中具有漂移的指数布朗运动；模拟股票价格的未来分布，以预测股票的未来价值

2024-03-09 15:20
文章标签 python 股票 具有 分布 未来 模拟 预测 指数 价值 股票价格 漂移 布朗运动

本文主要是介绍Python 中具有漂移的指数布朗运动；模拟股票价格的未来分布，以预测股票的未来价值，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、说明

        随机过程是由概率定律生成的一系列事件或路径。也就是说，随机事件可以随着时间的推移而发生，但受特定的统计和概率规则的约束。主要的随机过程是随机游走或布朗运动。这个过程可以用来预测许多变量，这些变量似乎遵循随机趋势，但受到概率定律的限制。
图片来源：内在价值

二、赋予动机

        为了预测股票的未知未来价值，我将在本文中展示一个与路径无关的 Python 蒙特卡罗模拟，以使用称为指数布朗运动（随机游走）过程的随机过程来模拟股票价格的未来分布。

        预测是预测未来的行为，无论是基于历史数据还是在没有历史存在的情况下对未来的猜测。当存在历史数据时，定量或统计方法是最好的，但如果不存在历史数据，那么定性或判断性方法通常是唯一的手段。

三、使用随机过程进行预测的基础知识

        随机过程只不过是一个数学定义的方程，可以随着时间的推移产生一系列结果，这些结果本质上不是确定性的。也就是说，它不遵循任何简单的可识别规则，例如价格每年将增加 X 个百分点，或者收入将增加 X 加 Y 个百分点。

        根据定义，随机过程是不确定的，可以将数字代入随机过程方程中，每次都获得不同的结果。例如，股票价格的路径本质上是随机的，人们无法可靠地预测确切的股票价格路径。

        然而，价格随时间的演变被包裹在产生这些价格的过程中。这个过程是固定的和预先确定的，但结果不是。

        因此，通过随机模拟，我们创建了多个价格路径，获得了这些模拟的统计样本，并根据用于生成时间序列的随机过程的性质和参数，对实际价格可能采取的潜在路径进行推断。

四、随机游走：布朗运动

图1

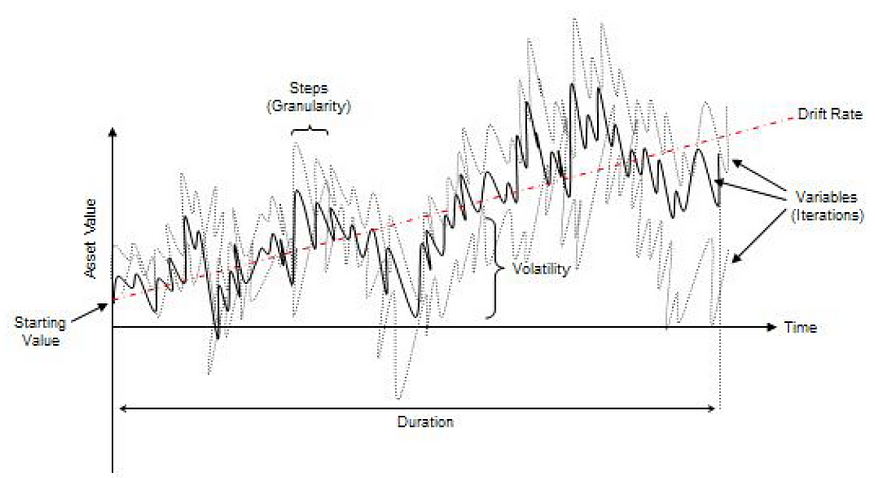
         假设一个过程 X，其中

图2

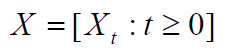
         当且仅当

图3

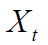
        是连续的，且起点是

图4

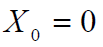
        其中 X 呈正态分布，均值为零，方差为 1 或

图5

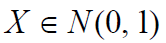
        并且时间上的每个增量都依赖于每个先前的增量，并且本身正态分布，均值零和方差 t，使得

图6

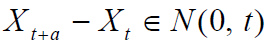
         然后，过程

图7

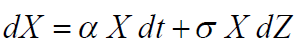
遵循指数布朗运动，其中α是漂移参数，σ波动性度量，并且

图8

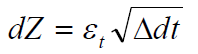
        这样

图9

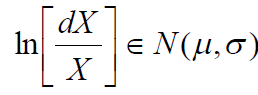
        或 X 和 dX 对数呈正态分布。

        如果在时间零，

图10
​​​​​​​

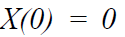
        则过程 X 在任何时候的期望值 t 是这样的

图11
 

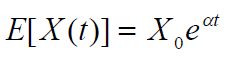
        过程 X 在任何时候的方差 t 为

图12

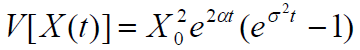
在α存在漂移参数的连续情况下，预期值变为

图13
 

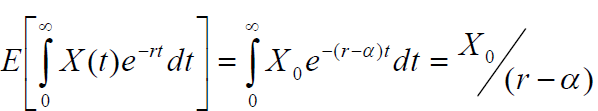
五、指数布朗运动（随机游走）过程

未知未来值的路径无关指数布朗运动（随机游走）过程采用以下形式

Figure 14

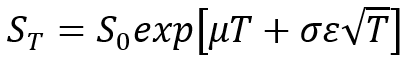
for regular options simulation, or a more generic version takes the form of

Figure 15

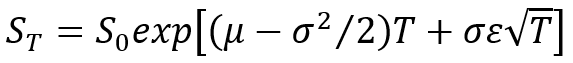
where

S0 = the variable’s today value (a.k.a starting value).

T = the forecast horizon (years).

ST = the variable’s future value T years from today (a.k.a final value).

μ = 年化增长率或漂移率。

σ = 年化波动率。

ε = 来自标准化正态分布 Φ（0， 1） 的随机抽取。

为了从一组时间序列数据中估计参数，漂移率μ为相对回报的平均值

图16

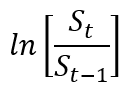
而σ是所有

图17

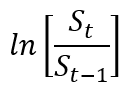
值。

六、蒙特卡罗模拟

蒙特卡罗模拟通常用于没有分析解且其他方法（如二项式树）不太合适的情况。

当用于预测股票的未来价值时，蒙特卡罗模拟使用真实世界的估值结果。现实世界的估值意味着股票的平均增长率必须高于无风险资产。因此，现实世界估值下的漂移率是股票的预期回报率，而风险中性估值/世界下的漂移率是无风险率。

我们对路径进行采样，以获得现实世界中的预期未来价值。考虑今天值为 S0 的股票 S，我们希望从今天起预测其未来价值 T 年。假设预期收益和波动率是恒定的，我们可以预测从今天起股票T年的未来价值如下：

  1. 在现实世界中对 S 的随机路径（也称为迭代）进行采样。
  2. 计算股票的未来价值。
  3. 重复步骤 1 和 2 以获取现实世界中股票未来价值的许多样本值。
  4. 计算样本未来值的平均值，以获得股票预期未来值的估计值。

假设现实世界中股票所遵循的未知未来价值的过程是

图18

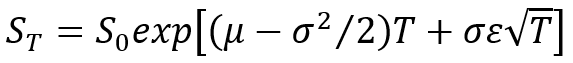
七、Python中的指数布朗运动

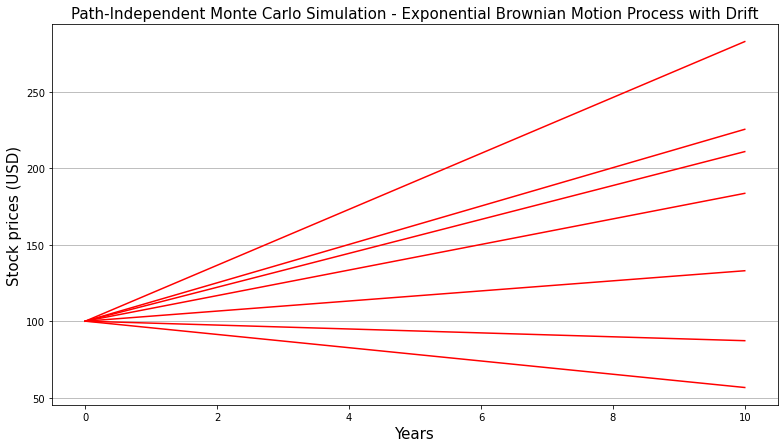
        考虑一只起始值为 100、漂移率为 5%、年化波动率为 25% 和预测期限为 10 年的股票。让我们根据这些参数和称为指数布朗运动（随机游走）和漂移的随机过程来预测 10 年后的股票未来价值。

        由于我们希望运行与路径无关的模拟，因此我们将仅使用一个时间步长。最后，我们将在计算中使用 50，000 次迭代。

        因此，S0 = 100，T = 10.0，μ = 0.05，σ = 0.25，N=1，M = 50，000

        首先，让我们加载相关的 python 库用于数据科学。

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from numpy import random as rn
from scipy import stats
import scipy.stats as si
import seaborn as sns
G = 1629562571
np.random.seed(G) 
from datetime import datetime
# datetime object containing current date and time
now = datetime.now()
dt_string = now.strftime("%d/%m/%Y %H:%M:%S")

        其次，让我们设置模型的参数。

S0 = 100
T = 10.0
μ = 0.05
σ = 0.25
M = 50000
N = 1
N

1

        第三，让我们为未来的值和随机绘图构建指标

ε = rn.randn(M,N)
S = S0*np.ones((M,N+1))
dt = T/N
dt

5

        第四，让我们构建模型

start_time = datetime.now() 
for i in range(0,N):S[:,i+1] = S[:,i]*np.exp( (μ-0.5*σ**2)*T + σ*ε[:,i]*np.sqrt(T) )

        第五，让我们可视化 8 条路径的模型结果

plt.figure(figsize=(13,7))
fontsize=15
plt.title('Path-Independent Monte Carlo Simulation - Exponential Brownian Motion with Drift',fontsize=fontsize)
plt.xlabel('Years',fontsize=fontsize)
plt.ylabel('Stock prices (USD)',fontsize=fontsize)
plt.grid(axis='y')
a = [ rn.randint(0,M) for j in range(1,8)]
for runer in a:plt.plot(np.arange(0,T+dt,dt), S[runer], 'red')
图 19
 第六  结果输出 
V = (S[:,-1])
print("\033[1m The estimate of the future value of the stock is ${:.2f}".format(np.mean(V)))
print("\033[1m The accuracy of the estimate of the future value of the stock is ${:.2f}".format((np.std(V)/np.sqrt(M))))

股票未来价值的估计为 164.78
美元 股票未来价值估计的准确率为 0.69 美元

第七，让我们打印内在值属性输出

time_elapsed = datetime.now() - start_time
def NORMSINV(x):x = si.norm.ppf(x)return (x)
Workbook_Name = "Exponential Brownian Motion with Drift.ipynb"
Number_of_Steps = "{:,.0f}".format(N)
Number_of_Iterations = "{:,.0f}".format(M)
Number_of_Inputs = "{:,.0f}".format(6)
Number_of_Outputs = 1
Sampling_Type = "Latin Hypercube"
Simulation_Start_Time = dt_string
Simulation_Duration = '{}'.format(time_elapsed)
Random_N_Generator = 'Mersenne Twister'
e = ['Workbook Name','Number of Steps','Number of Iterations','Number of Inputs','Number of Outputs','Sampling Type',\'Simulation Start Time','Simulation Duration','Random # Generator']
f = [Workbook_Name, Number_of_Steps, Number_of_Iterations, Number_of_Inputs, Number_of_Outputs, Sampling_Type,\Simulation_Start_Time, Simulation_Duration, Random_N_Generator]
Per5 = "{:,.1f}".format(np.percentile(V, 5))
P5 = "{:.0%}".format(0.05)
Per10 = "{:,.1f}".format(np.percentile(V, 10))
P10 = "{:.0%}".format(0.10)
Per15 = "{:,.1f}".format(np.percentile(V, 15))
P15 = "{:.0%}".format(0.15)
Per20 = "{:,.1f}".format(np.percentile(V, 20))
P20 = "{:.0%}".format(0.20)
Per25 = "{:,.1f}".format(np.percentile(V, 25))
P25 = "{:.0%}".format(0.25)
Per30 = "{:,.1f}".format(np.percentile(V, 30))
P30 = "{:.0%}".format(0.30)
Per35 = "{:,.1f}".format(np.percentile(V, 35))
P35 = "{:.0%}".format(0.35)
Per40 = "{:,.1f}".format(np.percentile(V, 40))
P40 = "{:.0%}".format(0.40)
Per45 = "{:,.1f}".format(np.percentile(V, 45))
P45 = "{:.0%}".format(0.45)
Per50 = "{:,.1f}".format(np.percentile(V, 50))
P50 = "{:.0%}".format(0.50)
Per55 = "{:,.1f}".format(np.percentile(V, 55))
P55 = "{:.0%}".format(0.55)
Per60 = "{:,.1f}".format(np.percentile(V, 60))
P60 = "{:.0%}".format(0.60)
Per65 = "{:,.1f}".format(np.percentile(V, 65))
P65 = "{:.0%}".format(0.65)
Per70 = "{:,.1f}".format(np.percentile(V, 70))
P70 = "{:.0%}".format(0.70)
Per75 = "{:,.1f}".format(np.percentile(V, 75))
P75 = "{:.0%}".format(0.75)
Per80 = "{:,.1f}".format(np.percentile(V, 80))
P80 = "{:.0%}".format(0.80)
Per85 = "{:,.1f}".format(np.percentile(V, 85))
P85 = "{:.0%}".format(0.85)
Per90 = "{:,.1f}".format(np.percentile(V, 90))
P90 = "{:.0%}".format(0.90)
Per95 = "{:,.1f}".format(np.percentile(V, 95))
P95 = "{:.0%}".format(0.95)
Minimum = "{:,.1f}".format(np.min(V))
Maximum = "{:,.1f}".format(np.max(V))
Mean = "{:,.1f}".format(np.mean(V))
Std_Dev = "{:,.1f}".format(np.std(V))
Variance = int(np.var(V))
Std_Error = "{:,.1f}".format(np.std(V)/np.sqrt(M))
Skewness = round(stats.skew(V),9)
Kurtosis = round((stats.kurtosis(V)+3),9)
Median = "{:,.1f}".format(np.median(V))
Mode = "{:,.1f}".format(stats.mode(V)[0][0])
Left_X = Per5
Left_P = P5
Right_X = Per95
Right_P = P95
Diff_X = "{:,.1f}".format((np.percentile(V, 95) - np.percentile(V, 5)))
Diff_P = "{:.0%}".format(0.90)
Confidence_Level = P95
Lower_Bound = "{:,.1f}".format((np.mean(V) - (np.std(V)/np.sqrt(M))*NORMSINV(0.975)))
Upper_Bound = "{:,.1f}".format((np.mean(V) + (np.std(V)/np.sqrt(M))*NORMSINV(0.975)))
g = {'Information': e, 'Result': f}
st = pd.DataFrame(data=g)
a = ['Minimum','Maximum','Mean','Std Dev','Variance','Std Error', 'Skewness','Kurtosis','Median','Mode',\'Left X','Left P','Right X','Right P','Diff X','Diff P','Confidence Level','Lower 95.0%','Upper 95.0%']
b = [Minimum, Maximum, Mean, Std_Dev, Variance, Std_Error, Skewness, Kurtosis, Median, Mode, Left_X, Left_P,\Right_X, Right_P, Diff_X, Diff_P, Confidence_Level, Lower_Bound, Upper_Bound]
c = [P5,P10,P15,P20,P25,P30,P35,P40,P45,P50,P55,P60,P65,P70,P75,P80,P85,P90,P95]
d = [Per5, Per10, Per15, Per20, Per25, Per30, Per35, Per40, Per45, Per50, Per55, Per60, Per65,\Per70, Per75, Per80, Per85, Per90, Per95]
d = {'Statistics': a, 'Statistics Result': b, 'Percentile': c, 'Percentile Result': d}
st1 = pd.DataFrame(data=d)
from datetime import date
today = date.today()
now = datetime.now()
import calendar
curr_date = date.today()
print("\033[1m Simulation Summary Information")
print("\033[0m ================================================")
print("\033[1m Performed By:","\033[0mIntrinsic Value Team #1")
print("\033[1m Date:","\033[0m",calendar.day_name[curr_date.weekday()],",",today.strftime("%B %d, %Y"),",",now.strftime("%H:%M:%S AM"))
st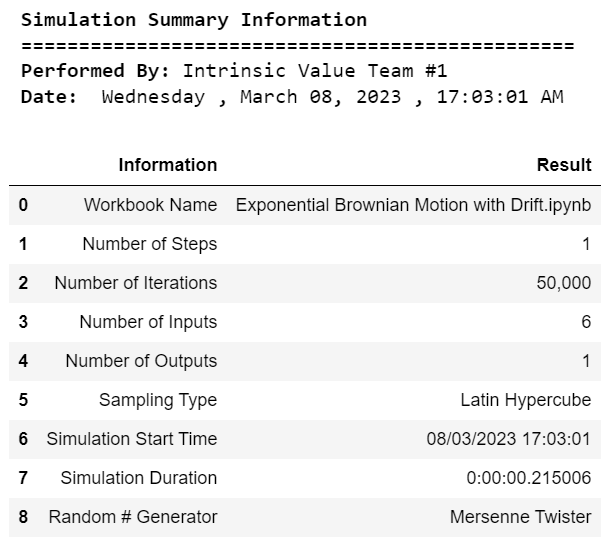

图20 
print("\033[1m Summary Statistics for Future Value of Stock")
print("\033[0m ======================================================")
print("\033[1m Performed By:","\033[0mIntrinsic Value Team #1")
print("\033[1m Date:","\033[0m",calendar.day_name[curr_date.weekday()],",",today.strftime("%B %d, %Y"),",",now.strftime("%H:%M:%S AM"))
st1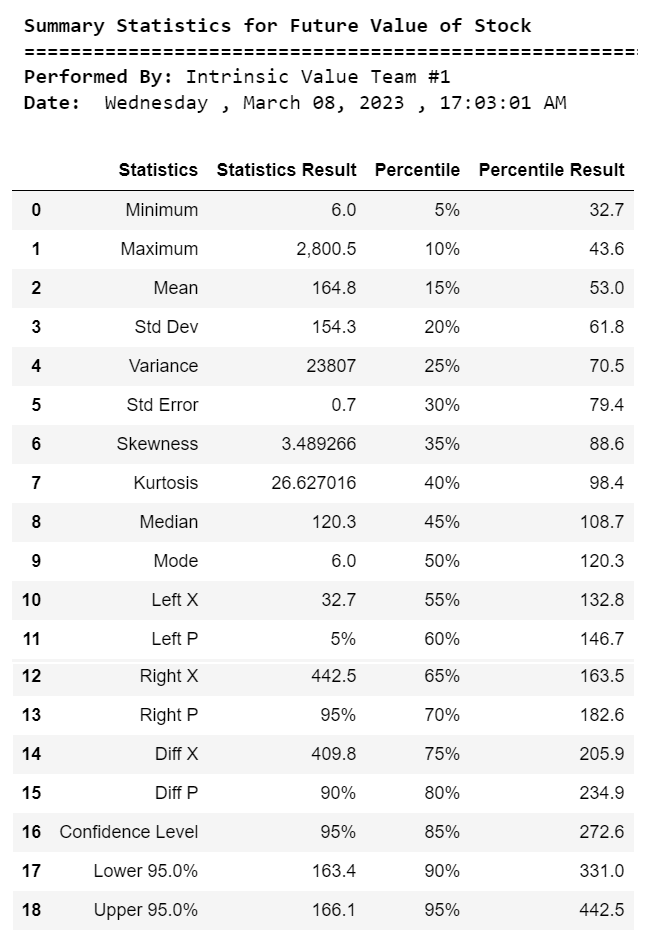

图21 
plt.figure(figsize = (4,4))
sns.set(font_scale = 1.2)
sns.set_style('white')
ax = sns.histplot(data=V,bins=50,color='red')
ax.set_xlabel('Values',fontsize=14)
ax.set_xlim( np.percentile(V, 0) , np.percentile(V, 99) )
print("\033[1m Probability Density Function for Future Value of Stock (Sim#1)")
print("\033[0m ======================================================")
print("\033[1m Performed By:","\033[0mIntrinsic Value Team #1")
print("\033[1m Date:","\033[0m",calendar.day_name[curr_date.weekday()],",",today.strftime("%B %d, %Y"),",",now.strftime("%H:%M:%S AM")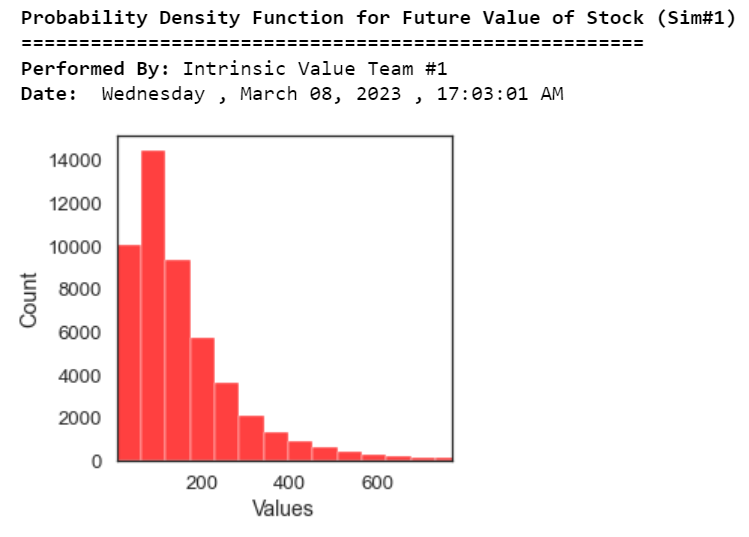

图22 
plt.figure(figsize = (4,4))
kwargs = {'cumulative': True}
sns.set(font_scale = 1.2)
sns.set_style('white')
ax = sns.ecdfplot(V, color='red')
ax.set_xlabel('Values',fontsize=14)
ax.set_xlim( np.percentile(V, 0) , np.percentile(V, 99) )
print("\033[1m Cumulative Distribution Function for Future Value of Stock (Sim#1)")
print("\033[0m ======================================================")
print("\033[1m Performed By:","\033[0mIntrinsic Value Team #1")
print("\033[1m Date:","\033[0m",calendar.day_name[curr_date.weekday()],",",today.strftime("%B %d, %Y"),",",now.strftime("%H:%M:%S AM"))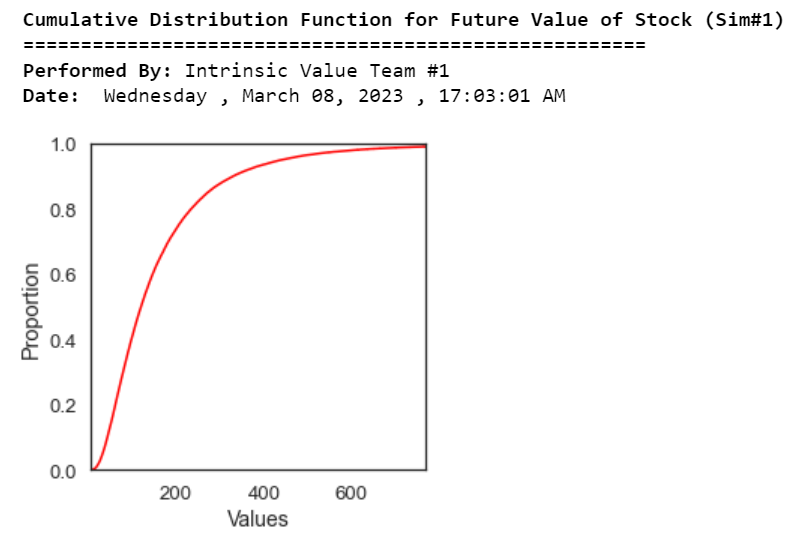

图23

八、总结

        蒙特卡罗模拟涉及使用随机数对股票价格在现实世界中可能遵循的许多不同路径（迭代）进行采样。对于每个路径，将计算未来值。未来价值的算术平均值是股票的预测未来价值。

样本均值的标准误差通常用作模型精度水平的指示。由于此标准误差随着路径数量的增加而下降非常缓慢，因此通常需要使用数万条（甚至更多）的样本路径才能达到可接受的精度水平。

参考：

·

Python 中具有漂移过程的指数布朗运动（随机游走） |中等 (medium.com)

这篇关于Python 中具有漂移的指数布朗运动；模拟股票价格的未来分布，以预测股票的未来价值的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/791079。

相关文章

使用Python绘制蛇年春节祝福艺术图

使用Python绘制蛇年春节祝福艺术图

《使用Python绘制蛇年春节祝福艺术图》：本文主要介绍如何使用Python的Matplotlib库绘制一幅富有创意的“蛇年有福”艺术图,这幅图结合了数字,蛇形,花朵等装饰,需要的可以参考下... 目录1. 绘图的基本概念2. 准备工作3. 实现代码解析3.1 设置绘图画布3.2 绘制数字“2025”3.3
阅读更多...
python使用watchdog实现文件资源监控

python使用watchdog实现文件资源监控

《python使用watchdog实现文件资源监控》watchdog支持跨平台文件资源监控,可以检测指定文件夹下文件及文件夹变动,下面我们来看看Python如何使用watchdog实现文件资源监控吧... python文件监控库watchdogs简介随着Python在各种应用领域中的广泛使用，其生态环境也
阅读更多...
Python中构建终端应用界面利器Blessed模块的使用

Python中构建终端应用界面利器Blessed模块的使用

《Python中构建终端应用界面利器Blessed模块的使用》Blessed库作为一个轻量级且功能强大的解决方案,开始在开发者中赢得口碑,今天,我们就一起来探索一下它是如何让终端UI开发变得轻松而高... 目录一、安装与配置：简单、快速、无障碍二、基本功能：从彩色文本到动态交互1. 显示基本内容2. 创建链
阅读更多...
Java调用Python代码的几种方法小结

Java调用Python代码的几种方法小结

《Java调用Python代码的几种方法小结》Python语言有丰富的系统管理、数据处理、统计类软件包,因此从java应用中调用Python代码的需求很常见、实用,本文介绍几种方法从java调用Pyt... 目录引言Java core使用ProcessBuilder使用Java脚本引擎总结引言python
阅读更多...
python 字典d[k]中key不存在的解决方案

python 字典d[k]中key不存在的解决方案

《python字典d[k]中key不存在的解决方案》本文主要介绍了在Python中处理字典键不存在时获取默认值的两种方法,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,... 目录defaultdict：处理找不到的键的一个选择特殊方法__missing__有时候为了方便起见，
阅读更多...
使用Python绘制可爱的招财猫

使用Python绘制可爱的招财猫

《使用Python绘制可爱的招财猫》招财猫,也被称为“幸运猫”,是一种象征财富和好运的吉祥物,经常出现在亚洲文化的商店、餐厅和家庭中,今天,我将带你用Python和matplotlib库从零开始绘制一... 目录1. 为什么选择用 python 绘制？2. 绘图的基本概念3. 实现代码解析3.1 设置绘图画
阅读更多...
Python pyinstaller实现图形化打包工具

Python pyinstaller实现图形化打包工具

《Pythonpyinstaller实现图形化打包工具》：本文主要介绍一个使用PythonPYQT5制作的关于pyinstaller打包工具,代替传统的cmd黑窗口模式打包页面,实现更快捷方便的... 目录1.简介2.运行效果3.相关源码1.简介一个使用python PYQT5制作的关于pyinstall
阅读更多...
使用Python实现大文件切片上传及断点续传的方法

使用Python实现大文件切片上传及断点续传的方法

《使用Python实现大文件切片上传及断点续传的方法》本文介绍了使用Python实现大文件切片上传及断点续传的方法,包括功能模块划分（获取上传文件接口状态、临时文件夹状态信息、切片上传、切片合并）、整... 目录概要整体架构流程技术细节获取上传文件状态接口获取临时文件夹状态信息接口切片上传功能文件合并功能小
阅读更多...
python实现自动登录12306自动抢票功能

python实现自动登录12306自动抢票功能

《python实现自动登录12306自动抢票功能》随着互联网技术的发展,越来越多的人选择通过网络平台购票,特别是在中国,12306作为官方火车票预订平台,承担了巨大的访问量,对于热门线路或者节假日出行... 目录一、遇到的问题？二、改进三、进阶–展望总结一、遇到的问题？1.url-正确的表头：就是首先ur
阅读更多...
基于Python实现PDF动画翻页效果的阅读器

基于Python实现PDF动画翻页效果的阅读器

《基于Python实现PDF动画翻页效果的阅读器》在这篇博客中,我们将深入分析一个基于wxPython实现的PDF阅读器程序,该程序支持加载PDF文件并显示页面内容,同时支持页面切换动画效果,文中有详... 目录全部代码代码结构初始化 UI 界面加载 PDF 文件显示 PDF 页面页面切换动画运行效果总结主
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2