本文主要是介绍【数电复习】逻辑函数的表示方法及互相转换(表达式、真值表、逻辑图、波形图、卡诺图)(手把手教版(雾,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
#前言
一、逻辑函数表示方法的基本了解
1、逻辑函数表达式
2、真值表
3、逻辑图
逻辑运算
4、波形图
5、卡诺图(用来化简表达式,非常好使!!)
如何画出卡诺图
卡诺图的化简(十分重要!!!)
化简步骤
卡诺圈原则(重要!!)
二、逻辑表达式之间的转换
1、表达式 & 真值表
(1)表达式----->真值表
(2)真值表----->表达式
2、表达式 & 逻辑图
(1)表达式----->逻辑图
(2)逻辑图----->表达式
3、表达式 & 波形图
(1)表达式----->波形图
(2)波形图----->表达式
4、表达式 & 卡诺图
(1)逻辑函数----->卡诺图
如何变换为最小项表达式
最小项注意要点
(2)卡诺图----->表达式
【例题】
#前言
数电复习总结系列~~( ̄▽ ̄)~*内容大概包含了几种基本的逻辑函数表示方法的解析,以及他们的互相转换~~其中卡诺图化简什么的有很多注意事项要留意!!嗯唔其中也包含了最小项的一些注意点~~
因为这些属于计算的基础,所以非常重要~~ 不能错噢!要完全弄懂它φ(>ω<*) ~
一、逻辑函数表示方法的基本了解
1、逻辑函数表达式
(1)定义:逻辑函数表达式是用与、或、非等运算及组合起来,表示逻辑函数与逻辑变量之间关系的逻辑代数式
形同:
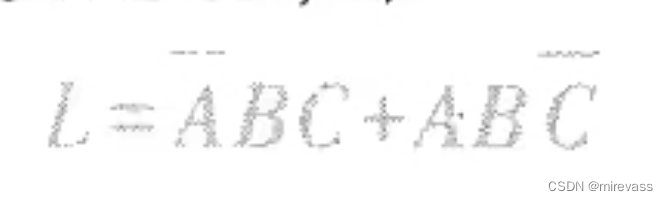
2、真值表
(1)定义:将输入变量所有可能的取值与相应的函数值列成的表格
注意:按二进制顺序取以避免遗漏
形同:
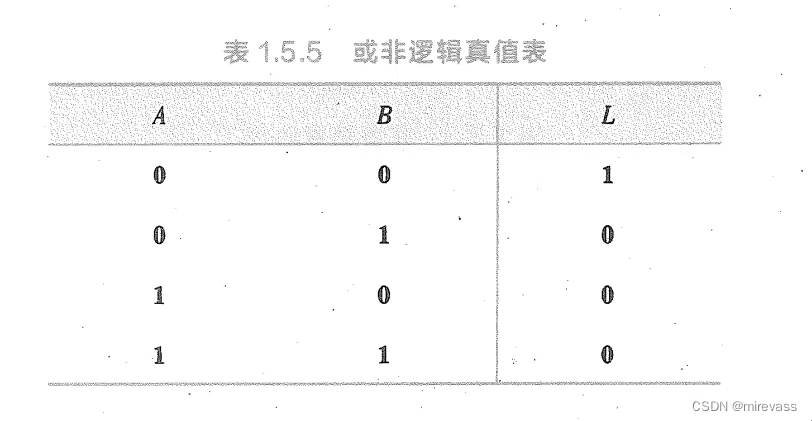
3、逻辑图
(1)定义:用与、或、非等逻辑符号表示逻辑函数中各变量之间的逻辑关系所得到的图形
(2)逻辑运算
①与运算
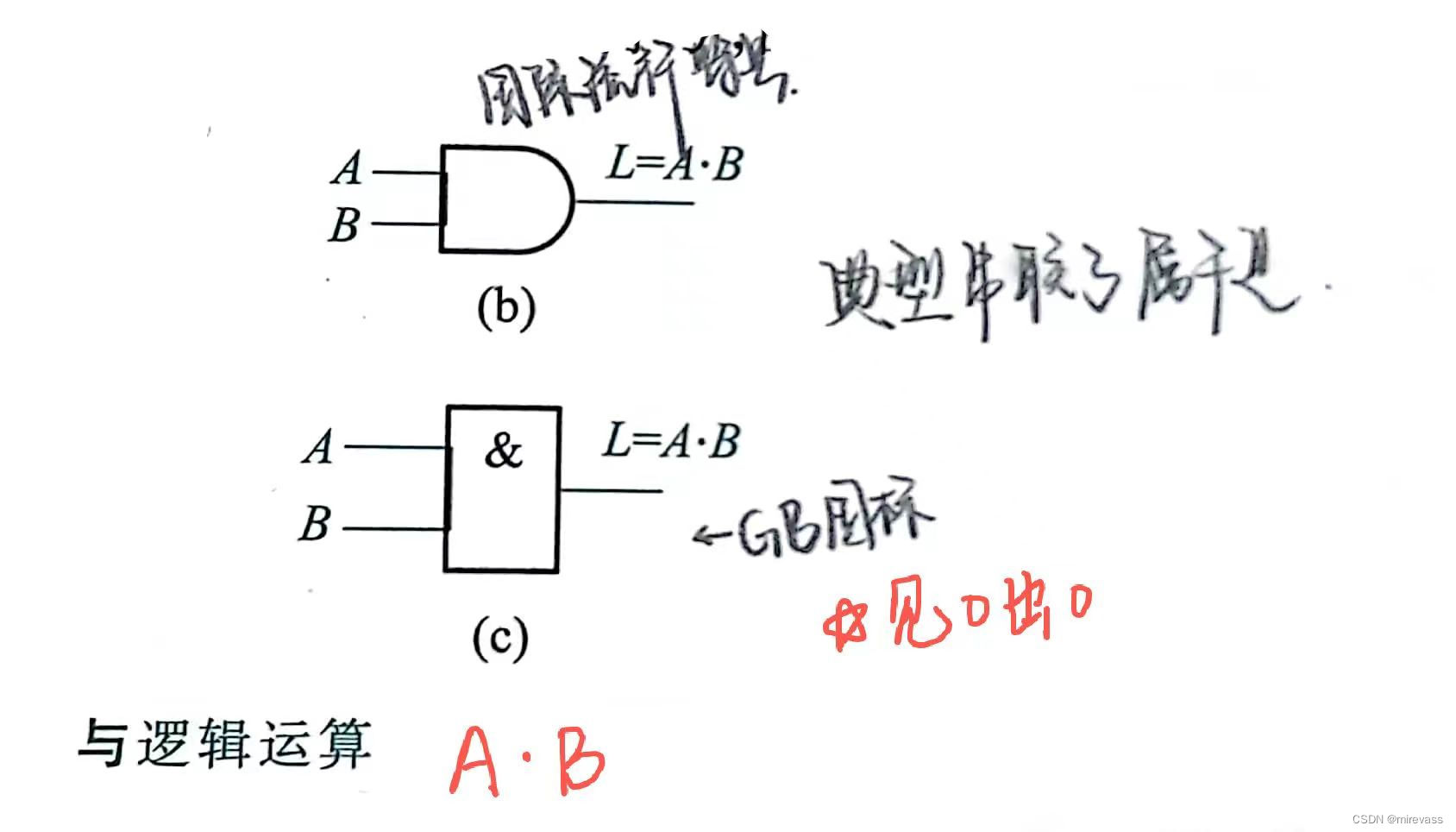
②或运算
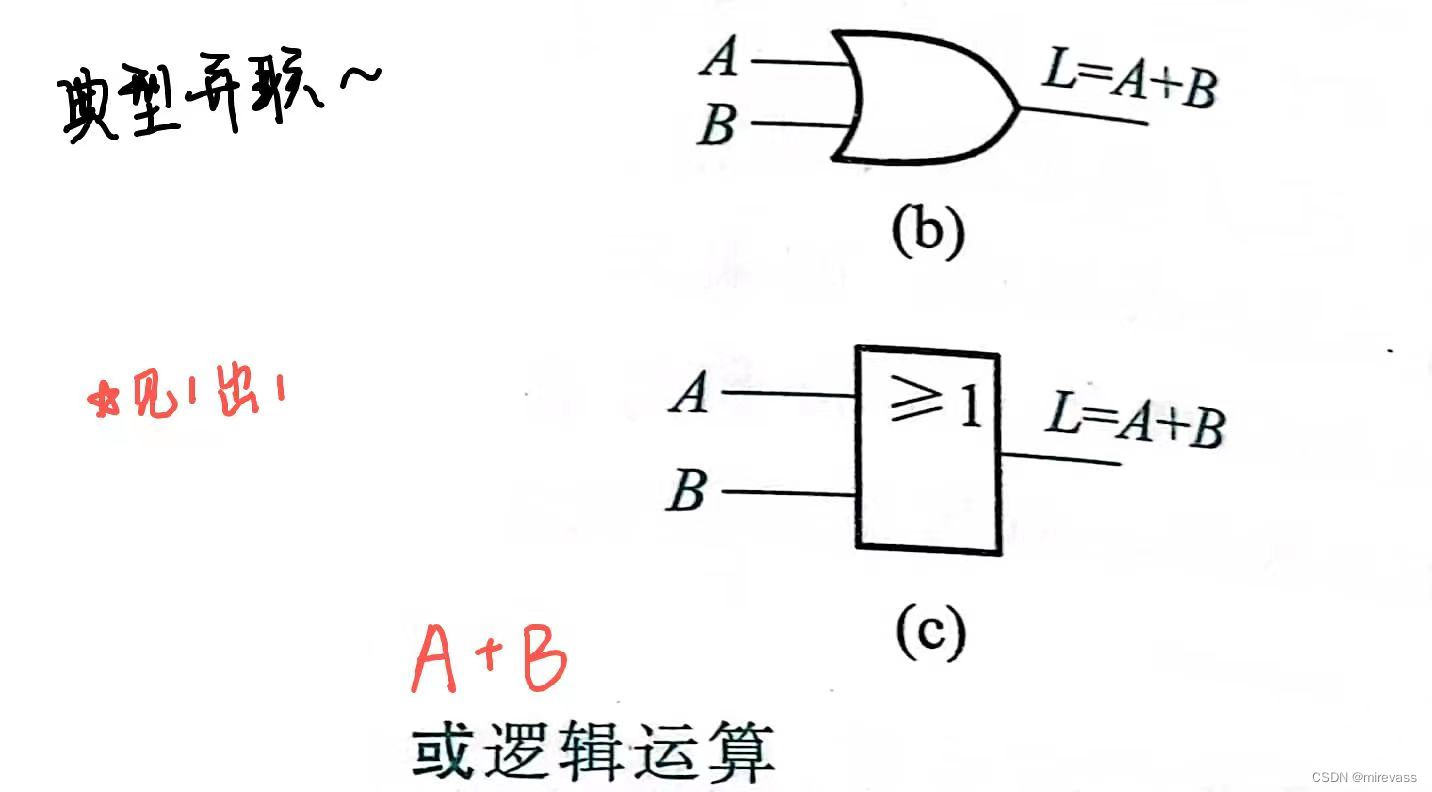
③非运算
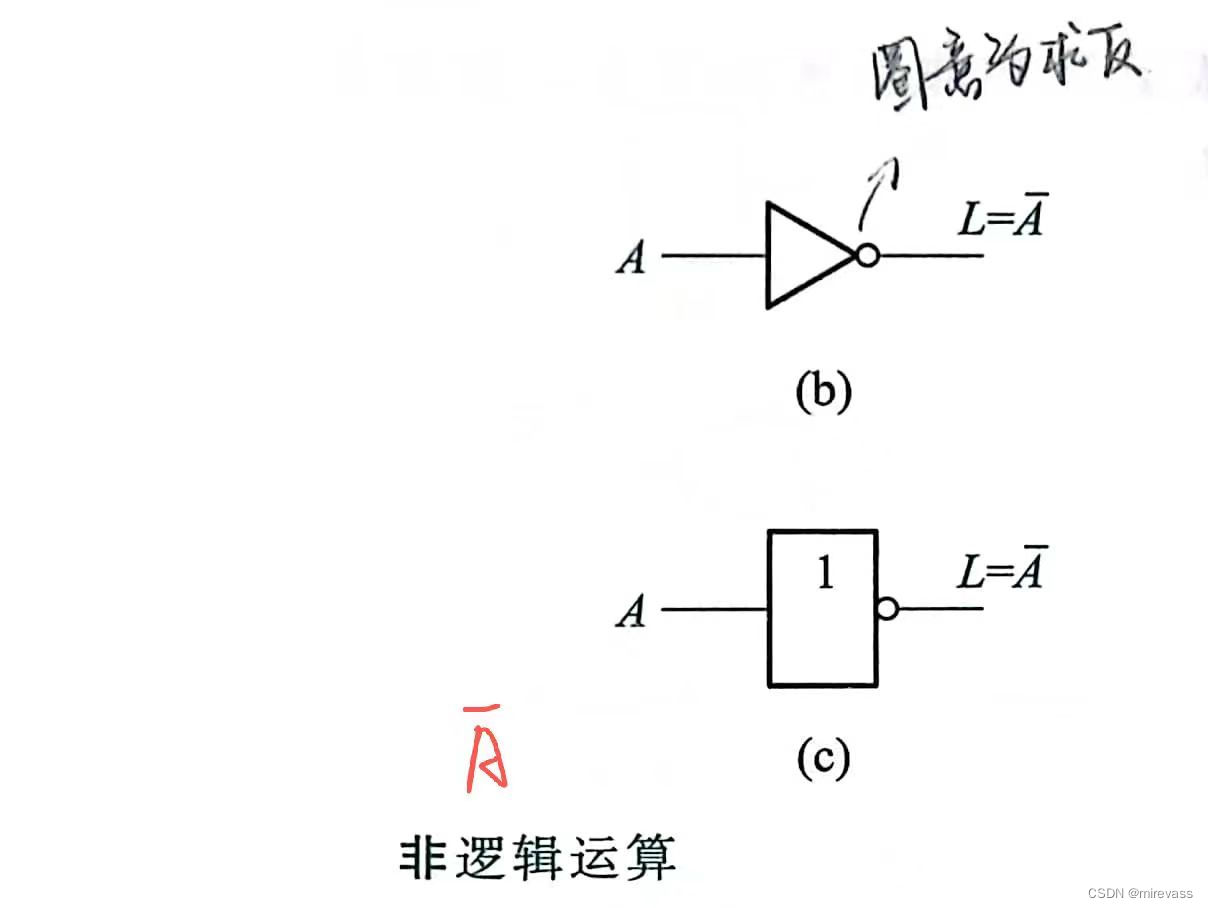
④ 常用复合逻辑运算
-与非
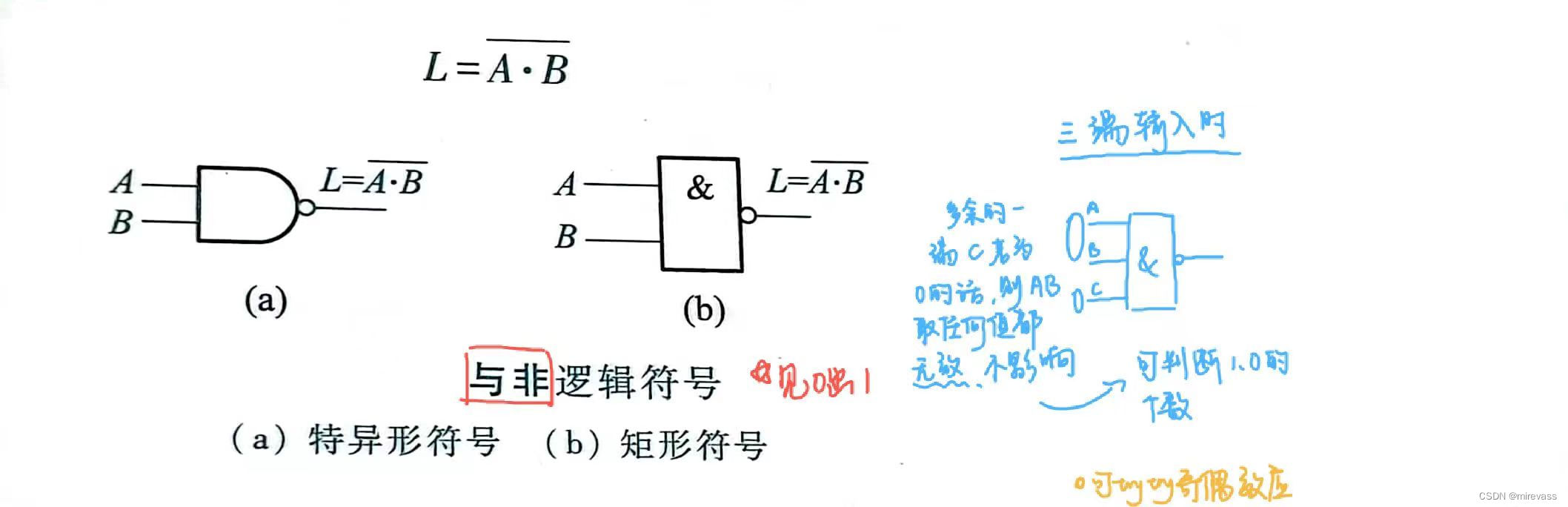
-或非
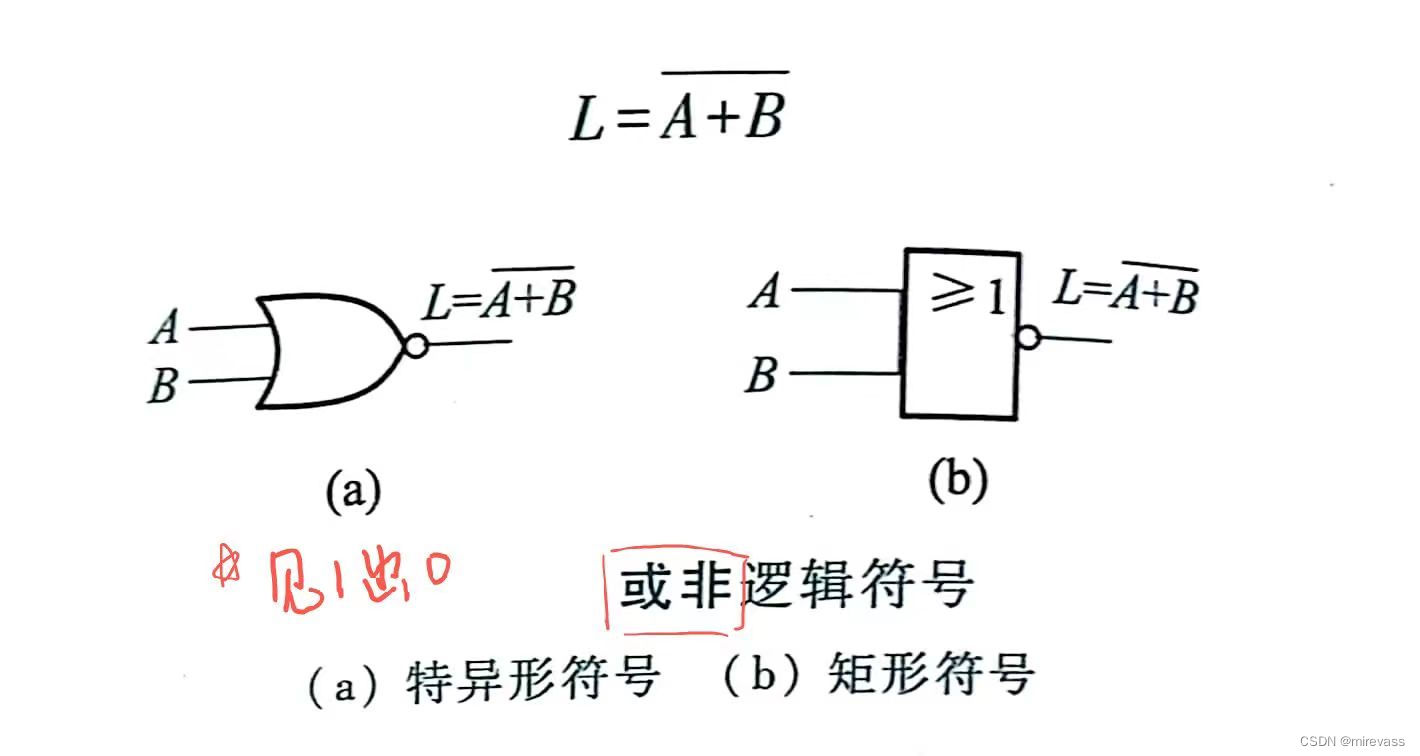
-异或
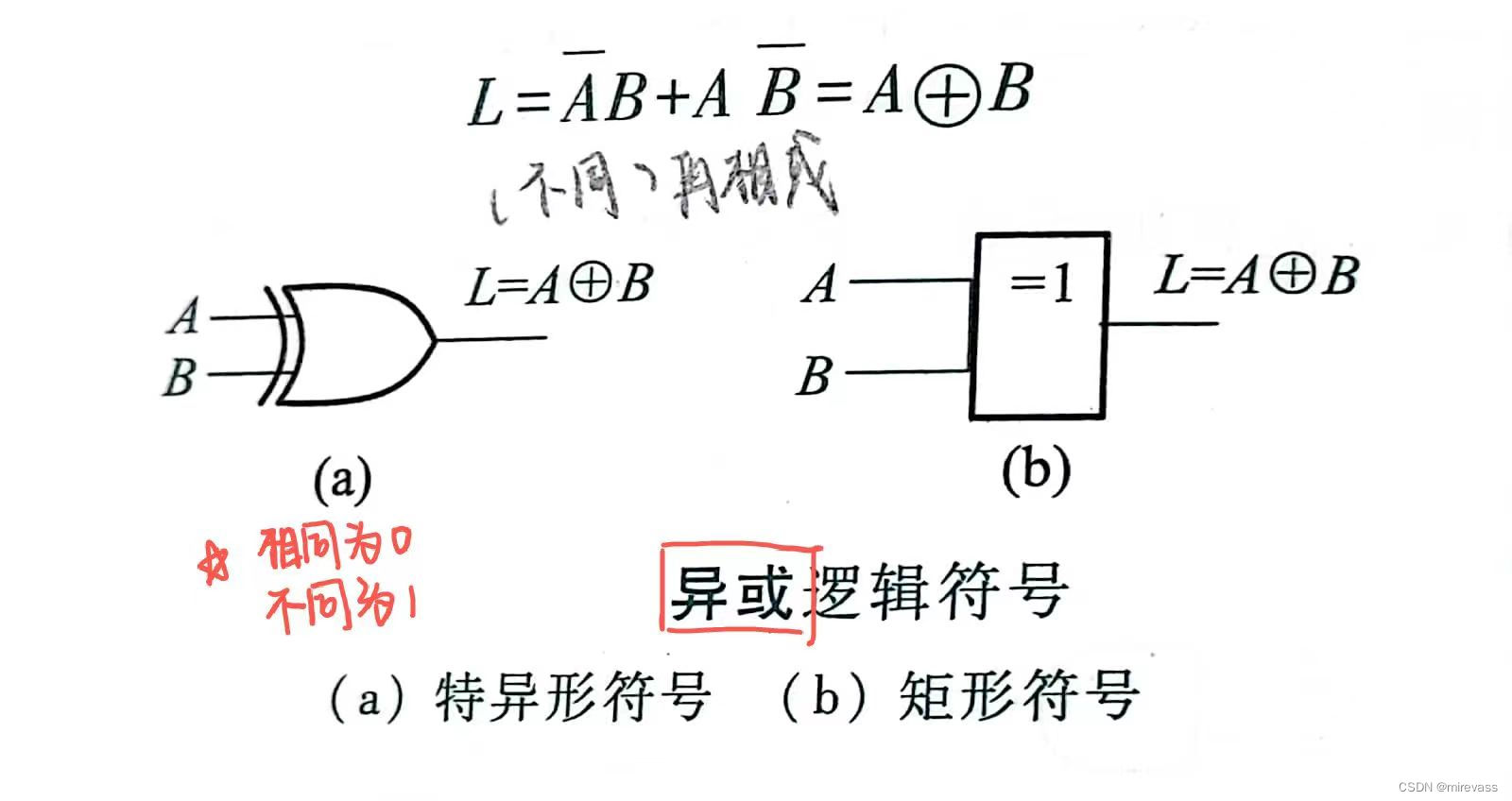
-同或
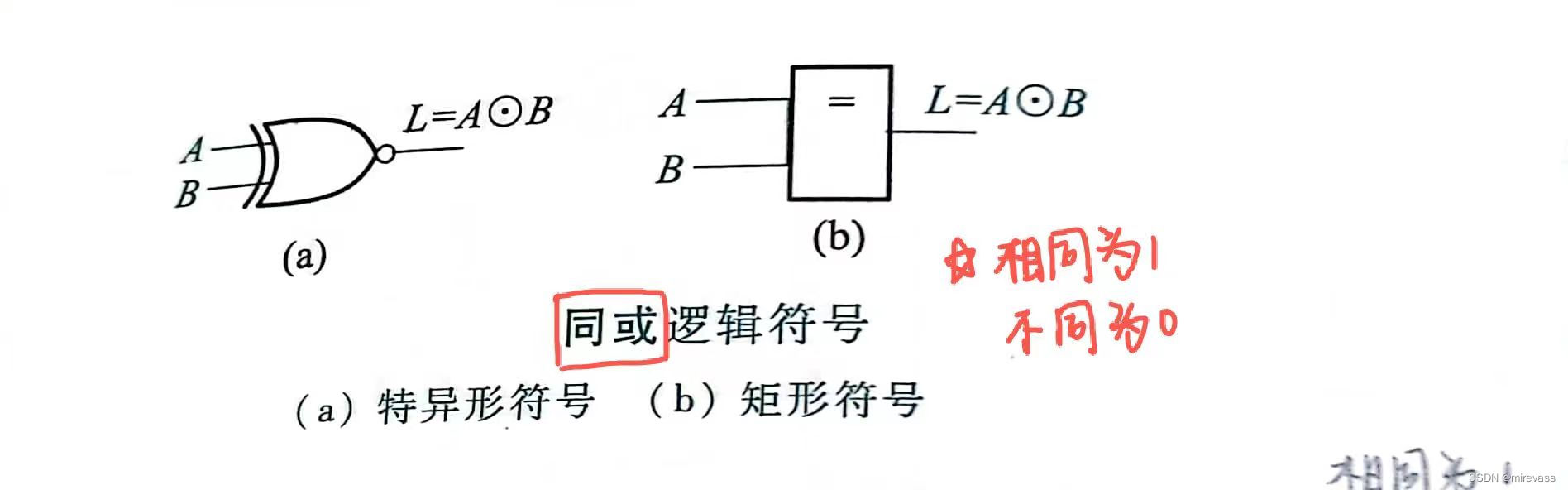
形同:
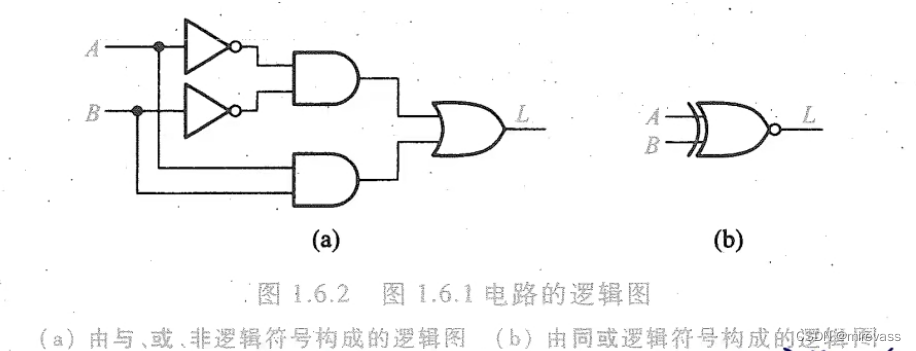
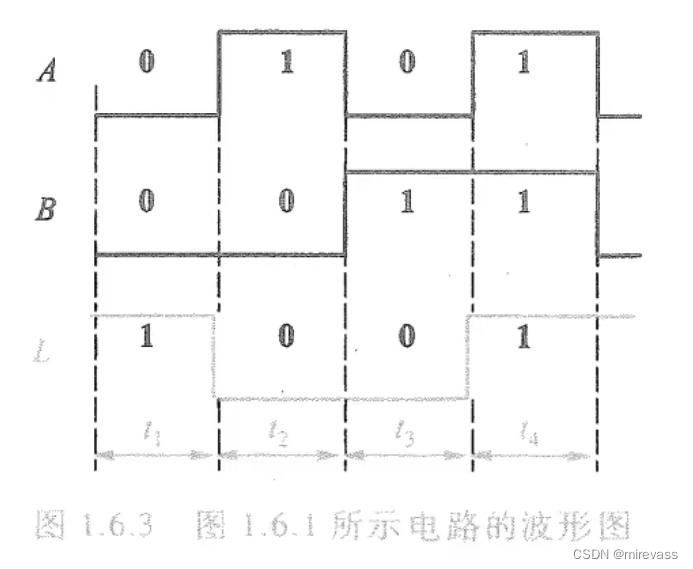
4、波形图
(1)定义:输入和输出关系按时间顺序依次排列得到的图形(对输入变量随时间变化的每一种取值,求出相应的输出值)
高电平为1,低电平为0;
形同:
5、卡诺图(用来化简表达式,非常好使!!)
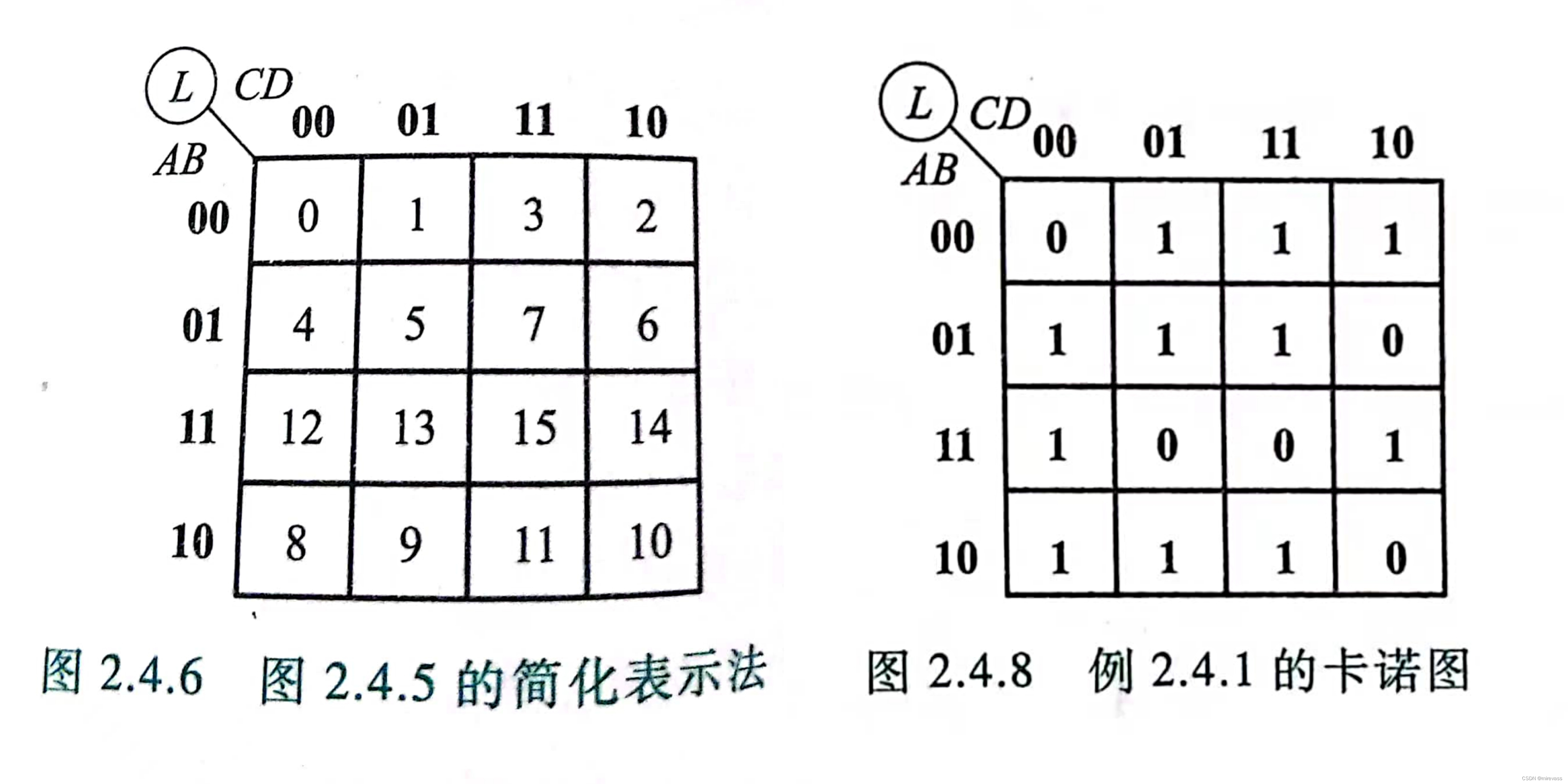
(1)定义:一个逻辑函数的卡诺图就是将此函数的最小项表达式中的各项最小项相应地填入一个特定的方格图内,此方格图为卡诺图
(卡诺图是真值表的图形化表示)
(2)特点:几何位置相邻的最小项在逻辑上也是相邻的。即相邻的两个最小项只有一个变量不同
注意:①对于n个变量的逻辑函数有 2ⁿ个最小项
②卡诺图相邻的数为格雷编码,即只有一位二进制数不同(01->11->10)
如下图:(左图为最小项的序号排列,右图为表达式对应的最小项)
(3)如何画出卡诺图(即 逻辑函数---->卡诺图)
(因为感觉卡诺图的转换比较重要!!ヾ(◍°∇°◍)ノ゙化简会一直使用到,所以就会在这里再赘述一遍~~)
①将逻辑函数的表达式变换为最小项表达式
②在卡诺图对应最小项的方格填上 1,其余的方格填上 0(或用空格表示),无关项用 x 表示,即可得
(也就是说任何逻辑函数都等于其卡诺图中为1的方格所对应的最小项之和)
(4)卡诺图的化简(十分重要!!!)
性质:卡诺图具有相邻性,若两个相邻的方格均为1,则这两个最小项之和有一个变量可以被消去
化简步骤:
①将逻辑函数写成最小项表达式(真值表可忽略步骤①,直接到步骤②)
②将最小项表达式中所含的最小项填入卡诺图中,有为1,无为0,无关为x
③找出为1的相邻最小项,画卡诺圈(从大往小的收!),每个卡诺圈含2ⁿ个方格,写出每个卡诺圈的乘积项(即 可以理解为 写出其中不变的变量)
④将所有卡诺圈对应的乘积项相加(可理解为,写出 "与"项之和 ,即与或式)
卡诺圈原则:(重要!!)
①卡诺圈内方格数必定是2ⁿ个
②相邻方格包括:上下底相邻、左右边相邻和四个角两两相邻
③同一个方格可以被不同的卡诺圈包围(即可 重复利用),但新增的卡诺圈不能相同必含有新方格,否则为多余
④卡诺圈内方格数尽可能多,卡诺圈数尽可能少(即 从大的往小的收,因为一个卡诺圈对应一个乘积项,卡诺圈越大,则所得乘积项中的变量越少;卡诺圈个数越少,则乘积项个数也越少,得到的 与-或 表达式 也最简)
⑤有的方格中的1被多个卡诺圈包含,并且每个标1的方格都有圈
⑥画卡诺圈时,尽可能考虑没有画过标1的方格
⑦化简得到的最简式不一定是唯一的
(可以用 德摩根定律 / 卡诺图取反 由 反函数的最简与或式 推到 最简或与式 )
(无关项的值,可取 0 也可取 1)
二、逻辑表达式之间的转换
可以将表达式看作转换的中介,其实本质上都是转换成表达式再作另外的转换(当然,其中的化简也是要注意的)
so,真值表转换到逻辑图 或者是 逻辑图转换到真值表 什么的 在这里就不多赘述了,本质上都一样的,以表达式为中介转换多一次就是了~(但为了逻辑图是最简的 为了实际运用到的零件最少最简化 中途对表达式的化简是必不可少的!!化简一律用卡诺图即可,因为公式)
1、表达式 & 真值表
(1)表达式----->真值表
方法:①确定(输入+输出)变量、函数
②赋值,得出真值表
(2)真值表----->表达式
方法:①找到真值表输出为1的行
②输入变量之间是与的关系,输出状态之间是或的关系
对于输入输出变量,取1值用原变量表示,取0值用反变量表示
③得出逻辑函数表达式并化简(最好用等式或卡诺图法化简)
(也可以理解为写出最小项表达式)
如下图:

2、表达式 & 逻辑图
(1)表达式----->逻辑图
方法:①将表达式中所有的与、或、非运算符号用相应的逻辑符号代替
②并按照逻辑运算先后次序将这些逻辑符号连接起来,即可得到对应逻辑图
注意:要先将逻辑表达式用公式法或卡诺图法化简再化成逻辑图
(2)逻辑图----->表达式
方法:①先确定输入变量与输出变量
②从输出倒推输入
(中间函数可以先用未知函数代替,最后溯回输入时再用输入变量去表示)
3、表达式 & 波形图
波形图转换成真值表时要注意!!若波形图中没有出现的某一最小项,说明这种输入组合不会出现,它所对应的输出是无关项,用x表示
(1)表达式----->波形图
方法:①按时间顺序画出输入与输出,高电平为1,低电平为0
(要将每种画出来,测试时若中间有缺也得把后面的另写出来)
(2)波形图----->表达式
因为直接从波形图很难看出表达式的逻辑关系,所以我们先转化成易得的真值表再由真值表转化为表达式
方法:①同理,高电平为1,低电平为0,写出真值表
②由真值表转化为表达式,即得
图略
4、表达式 & 卡诺图
画卡诺图时要注意!!如ABCD顺序的,若是自己设置的卡诺图,不是前面AB为竖列,后面CD为横列,那最小项序号不是横着来的,而是竖着来的,意思是要看到ABCD组合起来的数是几,它的最小项序号才是几,就是要看清楚高位在哪!!(本人亲身 痛 的经历~~(。•́︿•̀。)~~引以为戒~
(1)逻辑函数----->卡诺图
方法:①将逻辑函数的表达式变换为最小项表达式(使用摩根定理等来变换)
②在卡诺图对应最小项的方格填上 1,其余的方格填上 0(或用空格表示),无关项用 x 表示,即可得(真值表可忽略步骤①,直接到步骤②)
(也就是说任何逻辑函数都等于其卡诺图中为1的方格所对应的最小项之和)
然后在卡诺图化简中,如何得出最小项表达式也是非常重要的一个点,所以这里顺便将如何得到最小项表达式简述一下~(如果之后有时间 可能会出一个专门关于变换到最小项表达式的讲解与例题~)
如何变换为最小项表达式:
①先将表达式拆成最简与或式(用摩根定理等,非-只能在单个变量上,需去掉所有括号)
②将最简与或式配成为最小项表达式(缺什么补什么)
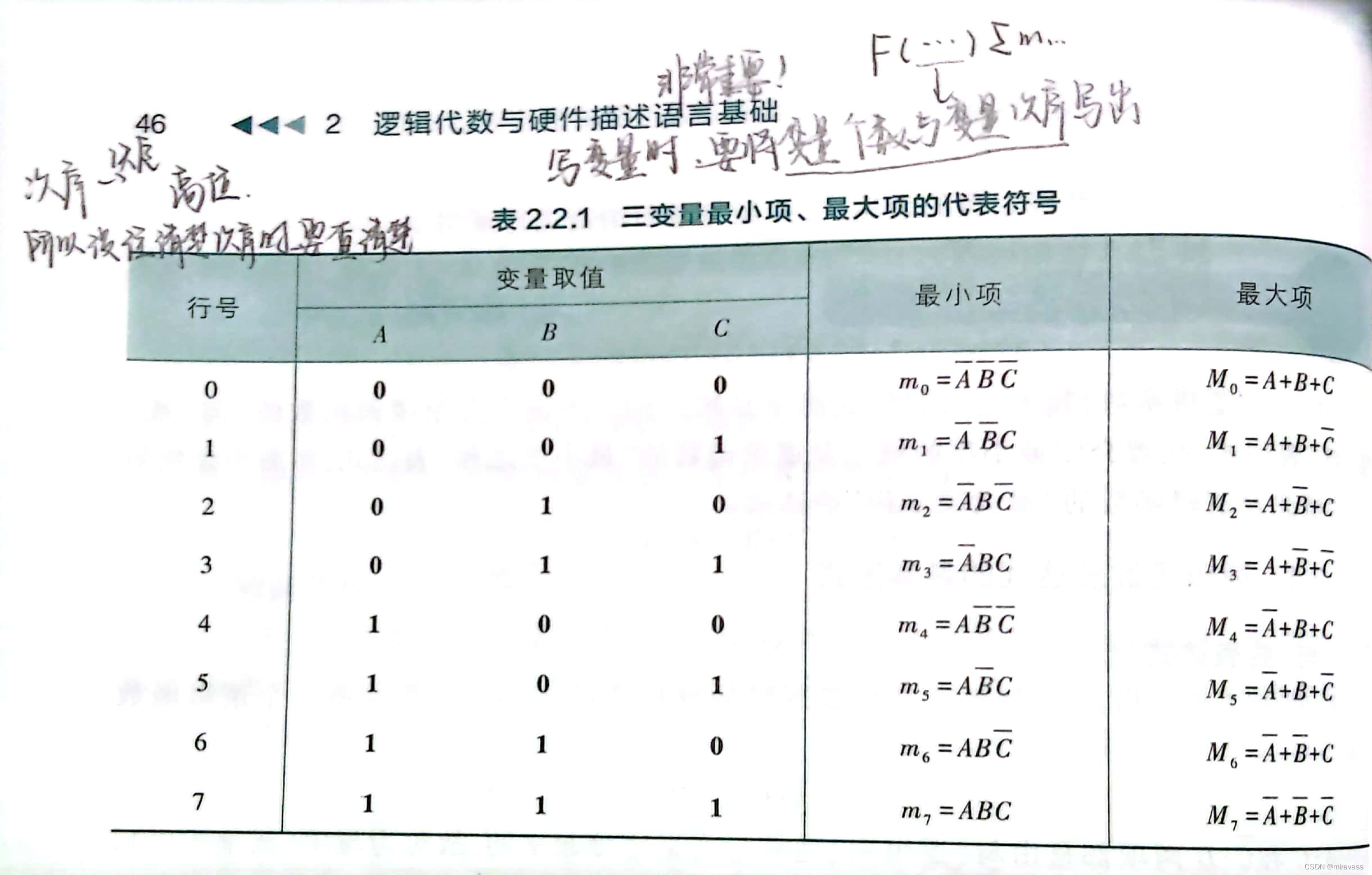
最小项注意要点:
①次序次序次序十分重要!!!写变量时要将变量个数与变量次序写出!
②次序决定着高位!!所以有没标注清楚次序时,要查清楚哪个是高位!!
如下图:(A为高位,C为低位,次序为ABC)
(2)卡诺图----->表达式
方法:①通过对卡诺图的化简得到最简与-或式(化简要求如上文所述)
【例题】
里面会包含卡诺图跟表达式的互相转换,就不单独拿单向转换的题来说了~~
解析:

好像有点点歪QAQ~
这篇关于【数电复习】逻辑函数的表示方法及互相转换(表达式、真值表、逻辑图、波形图、卡诺图)(手把手教版(雾的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




