巴特沃斯滤波器原理及其仿真设计

本文主要是介绍巴特沃斯滤波器原理及其仿真设计，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前面的几篇文章对一阶低通滤波器原理及其数字化进行了探究。为了进一步探究滤波这条知识线路，今天对巴特沃斯滤波器滤波器进行了研究。

1、什么是巴特沃斯滤波器？

巴特沃斯（Butterworth）滤波器是一种具有最大平坦幅度响应低通滤波器，它在通信领域里已有广泛应用，在电测中也具有广泛的用途，可以作检测信号的滤波器。文献［张殿龙王福文．巴特沃斯低通滤波器在电动机测试中的应用［J］成功地将巴特沃斯低通滤波器应用于电动机测试中。补充一下通带频率和阻带频率的概念，能够通过滤波器的频率信号范围构成通带（pass-bands）,而被衰减的频率信号则不能在输出端输出，这些被衰减的频率范围构成了滤波器的阻带（stop-bands）。通带与阻带交界点的频率称为截止频率。理想的滤波器其频率响应于通带区没有插入损耗(insertion-loss)，而于阻带则有无限大衰减以阻绝讯号通过。然而实际电路无法同时满足上述要求，故在设计电路时应选择适当滤波器种类以符合所需的规格。

2、巴特沃斯滤波器的特点

（1）最大平坦性。幅频特性的前２ｎ－１阶导数均为零，因此在截止频率前较为平坦，这个平坦也保证了信号的原始值，不会因为滤波被衰减。巴特沃斯低通滤波器的通频带最大扁平效应使通频带的增益得到扁平优化.

（2）幅频特性是单调下降，相频特性也是单调下降。巴特沃斯低通滤波器是全极点滤波器，所有零点都在无穷远处；它的幅度随频率的增加而单调下降，且频率无穷大时它的幅度才衰减完

（3）无论阶数ｎ是什么数，都会通过［ω＝ωｂ，｜Ｇ（ｊω）｜＝１／槡２］点。而且ｎ越大，其幅频响应就越逼近理想情况。

3、巴特沃斯滤波器的设计

在了解基本概念后，如何设计巴特沃斯滤波器滤波器是最关键的。对于巴特沃斯滤波器而言，n 阶巴特沃斯低通滤波器的振幅和频率关系可用如下的公式表示:

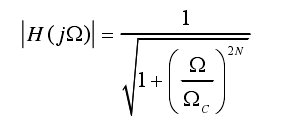
而巴特沃斯低通滤波器将其写为传递函数的形式，可以写为：

如果根据需要的截止频率、滤波器的阶数计算出上式中的所有系数b，即可完成对巴特沃斯滤波器的设计。以前其实是需要很完整的推导和计算的，现在matlab的实时更新对于巴特沃斯滤波器的工具箱进行充盈，在此记录一些工具函数的用法。

1、[N,wn]=buttord(wp,ws,rp,rs,'s') buttord函数

此函数的功能是根据数字滤波器的通带、阻带截止频率、通带衰减倍数、阻带衰减倍数来计算巴特沃斯数字滤波器的阶数N和3dB截止频率wn。

其中，调用参数wp，ws分别为数字滤波器的通带、阻带截止频率，当ws≤wp时，为高通滤波器；当wp和ws为二元矢量时，为带通或带阻滤波器，这时w n 也是二元向量。rp，rs分别为通带最大衰减和组带最小衰减（dB）。

2 [B，A]=butter（N，wn‘，ftype’）butter 函数

此函数的功能是根据滤波器阶数N和截止频率 wn计算N阶巴特沃斯数字滤波器系统函数分子、分母多项式的系数向量B、A。其中，调用参数N和wn分别为巴特沃斯数字滤波器的阶数和3 d B 截止频率，一般是可与buttord格式计算N和wn配合使用。系数B、A是按照z-1的升幂排列，ftype为滤波器的类型。N，wn为butter函数的调用参数。

3 buttap 函数 [Z，P，K] = buttap(N)

函数可设计出N阶巴特沃斯低通滤波器的零、极点。

以一个例子来说说这个滤波器的设计过程，由于芯片计算能力有限，假如我们需要一个二阶的巴特沃斯滤波器，并且截止频率也设定为100rad/s。那么此时就可以直接用[B，A]=butter（N，wn‘，ftype’）函数，输入代码如下：

N = 2;
wc = 100;
[B,A]= butter(N,wc,'s');  %代入N和wn设计低通巴特沃斯模拟滤波器
x = B
y = A
grid;

计算得出：

因此，此时可以得到传递函数的表达式如下所示：

4、巴特沃斯滤波器的性能测试

这个滤波器的优点好多地方已经介绍出来了，但是实际效果如何还是看波形最直接了，由于上述设计的巴特沃斯滤波器的截止频率为 100rad/s ，因此设计输入为幅值为100，频率为10rad/s初始正弦信号，叠加一个幅值为100，频率为100rad/s的正弦波。将叠加波分别通过截止频率为100rad/s的低通滤波器及巴特沃斯低通滤波器。其波形如下图所示，图中第一行波形为原始信号，第二行为一阶低通滤波器滤波后信号，第三行为二阶巴特沃斯低通滤波器后的信号，可以从仿真波形看到，巴特沃斯低通滤波器的性能要远优于一阶低通滤波器。