【马普所2008】机器学习中的核方法（上）

Hofmann T , Sch?Lkopf B , Smola A J . Kernel methods in machine learning[J]. Annals of Stats, 2008, 36(3).
[1] Integrating structured biological data by kernel
maximum mean discrepancy

本文是对于文献‘Kernel Methods in Machine Learning’的整理和总结。
该文章出版时间为2008年，比较久远，可以作为机器学习基础知识看待。

引入核方法的目的

1. 概括
   传统的机器学习理论和算法都是基于线性空间的，而实际问题中的数据分析问题通常需要使用非线性方法解决。而引入正定核可以在理论和实际问题中都达到最好的效果。

2. 基本原理
   正定核对应着特征空间的点乘。只要能够用核方法将everythhing都转化到特征空间，就可以在特征空间里用线性方法进行判别，而不需要对高维特征空间进行特殊计算。

核（尤其是正定核）的性质

介绍性的例子

1. 定义问题
   假设是二分类问题，有一组训练集有n个样本：(x1,y1),(x2,y2),…,(xn,yn)，y取值为{-1,1}。对于一个新的输入样本x，希望能预测对应的y，让（x，y）与训练样本相似。因此需要对xi所在的空间 X ，和yi所在的{-1,1}中元素的相似度进行衡量。后者显而易见，但前者需要定义函数：
   并且该函数满足：
   其中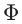将xi映射到点乘空间 H 中，也称为特征空间。
   也就是说，在 X 空间上的k(xi，xj)等价于在特征空间的点乘。

2. 结合图例
   
   对于上图的二分类问题，我们采用这样的分类方法，即，当新样本输入x对应的特征空间中的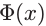更靠近训练样本中正类的均值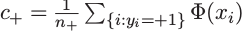时，认为其对应输出y=+1，反之亦然。
   因此用指示函数sgn(.)表示分类器为：
   * 与SVM关系
   分类器(5)与SVM有很强的联系。在特征空间，该分类器为显示为线性，但是在输入空间X中用核的扩展表示（represented by a kernel expansion）。相当于用特征空间里的超平面进行分类。SVM与（5）所示分类器的区别在于$w=c_{+}-c_{-}$的法向量上.

• 该法向量的方向决定了超平面的方向，长度决定了两个类别的生成分布。（？[1]）

• 分析
  c+、c-即为特征空间内两类样本点的均值，那么他们之间的连线的垂线（点虚线）就把整个特征空间分为两个部分，连线上到两个均值点距离相等，左边的点离c+更近，反之亦然。
  对应公式中的b，即为正负两类数据的均值在特征空间的点之间的差距的1/2，可以看做是向量 c-c+ 的一半，作用是将c±的中点移到原点，即将虚线、c±连线平移、旋转到与坐标轴重合的位置，方便使用指示函数。

3. 考虑特殊情况
   当b=0时，即当c-与c+连线中点与原点重合，用下式估计两个概率分布：
   那么分类器（5）就变成了贝叶斯决策法则（判断p+大则认为y=1，p-大则y=-1）.

正定核

引入问题

在上文中已经要求核满足下式，即让其与点积空间的点乘相对应 。那么在这一部分我们就要验证满足该式的这一类核是正定的。

首先引入一些定义

1. 格拉姆矩阵 (Gram matrix）

给定核k和输入$x1,...,xn\in$X，有nxn的矩阵K，元素Kij:= k(xi,xj），则称之为k的关于输入$x1,…, xn $的格拉姆矩阵。

2.正定核

实对称矩阵Kij，对于任意c$\in$R，有
则该矩阵为正定矩阵。若当且仅当c1=c2=…=cn=0时等号成立，则K为严格正定矩阵.

3. 正定核

假设X是非空集合，k是XxX→R的一个映射，对于任意n∈N，xi∈X，i∈[n],（[n]={1,2,3…,n})，都能够得到一个正定的格拉姆矩阵，则k称为正定核。
若得到的都是严格正定的格拉姆矩阵，则k称为严格正定核。

有时为了简略，我们会将正定核简称为核。为了简化，我们将问题限制在实数域上。然而，通过一些小的变化也可以扩展到复数域。

建立再生核希尔伯特空间

用核方法进行相关性估计和数据分析

再生核Hilbert空间在定义统计模型的应用

专业词汇

positive definite kernel 正定核
dot product space 点积空间