模糊PID控制算法实战讲解-案例温度控制（附C语言实现）

本文主要是介绍模糊PID控制算法实战讲解-案例温度控制（附C语言实现），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

 可结合之前的文章一起理解：

控制算法-PID算法总结-从公式原理到参数整定解析（附C源码）_pid自整定算法-CSDN博客

模糊控制算法实战讲解-案例温度控制（附C语言实现）-CSDN博客 

 

目录

一、模糊PID控制的原理

1.1 模糊化

1.2 模糊规则库

1.3 模糊推理

1.4  去模糊化

1.5 PID控制输入计算

二、特点和应用场景

三、案例温度控制

简化版本：

加入重心法后的模糊PID版本：

---

模糊PID控制算法是将传统的PID控制与模糊逻辑控制相结合的一种控制策略。这种算法尝试通过模糊逻辑系统来自动调整PID控制器的参数（比例系数Kp​、积分系数Ki​、微分系数Kd​），以适应系统动态变化的需求，从而提高控制系统的性能。模糊PID控制在处理非线性、时变系统或者模型不完全已知的系统时尤其有效。

一、模糊PID控制的原理

传统的PID控制器根据偏差e(t)（期望输出与实际输出之间的差值）和偏差的变化率e1(t)来计算控制输入。PID控制器的输出由三部分组成：比例（P）、积分（I）和微分（D）项，计算公式为：

                               

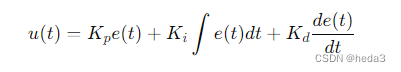
在模糊PID控制中，系统利用模糊逻辑根据当前的偏差e(t)和偏差变化率e1(t)来动态调整Kp​、Ki​、Kd​的值，以适应系统的变化。

1.1 模糊化

将偏差e(t)和偏差变化率e1(t)的精确值转换为模糊值，这些模糊值对应于模糊集合中的语言变量，例如“正大”、“正小”、“零”、“负小”、“负大”。

1.2 模糊规则库

建立一个模糊规则库，这些规则基于专家知识或经验，描述了在特定偏差和偏差变化率的情况下如何调整PID参数。例如：如果偏差是正大，且变化率是正小，则增大比例系数Kp​。

1.3 模糊推理

根据模糊化的输入e(t)和e1(t)）和模糊规则库，通过模糊推理得出每个PID参数的调整策略。

1.4  去模糊化

将模糊推理的结果转换为精确的PID参数值。

1.5 PID控制输入计算

使用调整后的PID参数计算控制输入u(t)

二、特点和应用场景

模糊PID控制器的主要优点是它结合了PID控制的直观性和模糊控制的适应性，能够在系统模型不完全已知或存在较大不确定性时提供良好的控制性能。控制更平稳。

应用场景：工业控制系统、机器人、汽车电子控制等领域

三、案例温度控制

考虑一个温度控制系统，其中模糊PID控制器用于调整加热器的功率输出，以维持设定的温度。根据温度偏差和偏差变化率的不同，模糊控制器会动态调整Kp​、Ki​、Kd​，以快速响应温度变化并减小超调，提高系统的稳定性和响应速度。

简化版本：

控制目标是使系统温度维持在一个设定值（比如25°C）。

PID参数（Kp​,Ki​,Kd​）需要根据温度偏差e(t)和偏差变化率e1(t)动态调整。

 PID控制器的结构体：

typedef struct {float Kp, Ki, Kd; // PID参数float integral;   // 积分项累计值float prev_error; // 上一次的偏差
} PIDController;

模糊规则：

void adjustPIDParams(PIDController* pid, float error, float delta_error) {// 假设根据偏差的大小和变化率调整PID参数// 这里的逻辑非常简化，实际应用中应该基于详细的模糊规则// 如果偏差大，增加Kp来快速减少偏差if (error > 5.0) pid->Kp += 0.1;else if (error < -5.0) pid->Kp -= 0.1;// 如果偏差变化快，增加Kd来减少超调if (delta_error > 0.5) pid->Kd += 0.05;else if (delta_error < -0.5) pid->Kd -= 0.05;// 保证PID参数在合理范围内if (pid->Kp < 0) pid->Kp = 0;if (pid->Kd < 0) pid->Kd = 0;
}

控制逻辑：

float computePIDOutput(PIDController* pid, float setpoint, float measured) {float error = setpoint - measured;float delta_error = error - pid->prev_error;// 简单的模糊逻辑调整PID参数adjustPIDParams(pid, error, delta_error);// 计算PID输出float output = pid->Kp * error + pid->Ki * pid->integral + pid->Kd * delta_error;// 更新状态pid->integral += error;pid->prev_error = error;return output;
}

int main() {PIDController pid = {0.1, 0.01, 0.05, 0, 0}; // 初始化PID参数和状态float setpoint = 25.0; // 目标温度float measured_temp = 20.0; // 测量温度，示例值// 模拟控制循环for (int i = 0; i < 100; ++i) {float control_signal = computePIDOutput(&pid, setpoint, measured_temp);// 应用control_signal到加热器...// 更新measured_temp...printf("Control Signal: %f\n", control_signal）

加入重心法后的模糊PID版本：

1）定义输入输出的模糊集合：

输入：温度误差e和误差变化率de。

每个输入都可以定义为几个模糊集合，例如：负大（NB），负小（NS），零（ZE），正小（PS），正大（PB）。

输出：PID参数的调整量，包括ΔKp、ΔKi和ΔKd。输出也可以定义为类似的模糊集合。

 2）定义隶属度函数：

   对于每个模糊集合，定义一个隶属度函数来量化一个具体的输入值属于该模糊集合的程度。隶属度函数可以是三角形、梯形或是其他形状。

3）模糊规则

• 基于经验或专家知识制定一组模糊规则，用于描述输入模糊集合之间的关系以及它们如何影响输出模糊集合。
• 例如：“如果e是PB并且de是ZE，则ΔKp是PB”。

4）去模糊化

 使用重心法（或其他去模糊化方法）将模糊输出转换为一个具体的数值，用于调整PID参数。

 只考虑e的影响，以kp的变化量调整为例：

#include <stdio.h>// 示例：简化的隶属度计算函数
float calculateMembership(float value, float min, float max) {if (value <= min) return 0;else if (value >= max) return 1;else return (value - min) / (max - min);
}// 示例：计算ΔKp的重心
float calculateDeltaKp(float e, float de) {// 示例：隶属度值计算（这里仅为示例，实际情况下更复杂）float eNB = calculateMembership(e, -10, -5);float eNS = calculateMembership(e, -5, -2);float eZE = calculateMembership(e, -2, 2);float ePS = calculateMembership(e, 2, 5);float ePB = calculateMembership(e, 5, 10);// 示例：简化的模糊规则处理，假设只根据e的模糊集合调整Kpfloat deltaKp = (eNB * -2) + (eNS * -1) + (eZE * 0) + (ePS * 1) + (ePB * 2);float totalMembership = eNB + eNS + eZE + ePS + ePB;// 重心法去模糊化return totalMembership > 0 ? deltaKp / totalMembership : 0;
}int main() {float e = -3;  // 示例误差值float de = 0;  // 示例误差变化率float deltaKp = calculateDeltaKp(e, de);printf("Calculated ΔKp: %f\n", deltaKp);return 0;
}

考虑e和de影响：

#include <stdio.h>// 示例：隶属度计算函数
float calculateMembership(float value, float min, float max) {if (value < min) return 0;else if (value > max) return 1;else return (value - min) / (max - min);
}// 示例：根据e和de的模糊规则计算ΔKp
float calculateDeltaKp(float e, float de) {// 隶属度值计算float eNB = calculateMembership(e, -10, -5);float deNB = calculateMembership(de, -10, -5);float eNS = calculateMembership(e, -5, -2);float deNS = calculateMembership(de, -5, -2);float eZE = calculateMembership(e, -2, 2);float deZE = calculateMembership(de, -2, 2);float ePS = calculateMembership(e, 2, 5);float dePS = calculateMembership(de, 2, 5);float ePB = calculateMembership(e, 5, 10);float dePB = calculateMembership(de, 5, 10);float deltaKpValues[] = {-2, -1, 0, 1, 2}; // 对应NB, NS, ZE, PS, PB// 模糊规则处理float rule1Output = eNB * deNB  * deltaKpValues[0]; // float rule2Output = eNS * deNS * deltaKpValues[1]; // float rule3Output = eZE * deZE * deltaKpValues[2]; // 如果e和de都是ZE，则ΔKp保持不变float rule4Output = ePS * dePS  * deltaKpValues[3]; //float rule5Output = ePB * dePB * deltaKpValues[4]; //// 假设这是根据所有规则计算出的ΔKp总和float deltaKpTotal = rule1Output+rule2Output +rule3Output +rule4Output +rule5Output ; float totalMembership = eNB +deNB +eNS + deNS +eZE + deZE+ePB +dePB ; // 重心法去模糊化return totalMembership > 0 ? deltaKpTotal / totalMembership : 0;
}int main() {float e = -1;  // 示例误差值float de = 1;  // 示例误差变化率float deltaKp = calculateDeltaKp(e, de);printf("Calculated ΔKp: %f\n", deltaKp);return 0;
}

这篇关于模糊PID控制算法实战讲解-案例温度控制（附C语言实现）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---