本文主要是介绍备战蓝桥杯Day19 - 堆排序基础知识,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、每日一题 - 填充

详细题解
s = input() # 输入字符串
n = len(s) # 定义字符的长度
judge = ["00", "11", "0?", "1?", "?0", "?1", "??"]
# 把所有的情况一一列举出来
count = 0 # 设置计数器
i = 1 # 设置循环条件索引值
while i < n:if s[i-1:i+1] in judge: # 在循环中将字符串遍历进行判断count += 1 # 如果符合计数器 + 1i += 2 # 并将索引值向后移动2个else:i += 1 # 不符合条件索引值向后移1个print(count) # 最后打印出结果我觉得最难的在于不纠结?到底是0还是1,而是直接把他看成数字去跟已知情况进行判断。我一直在纠结?到底应该什么时候是1,什么时候是0,把自己的思路的限制住了。
二、堆排序
预备基础知识 - 树
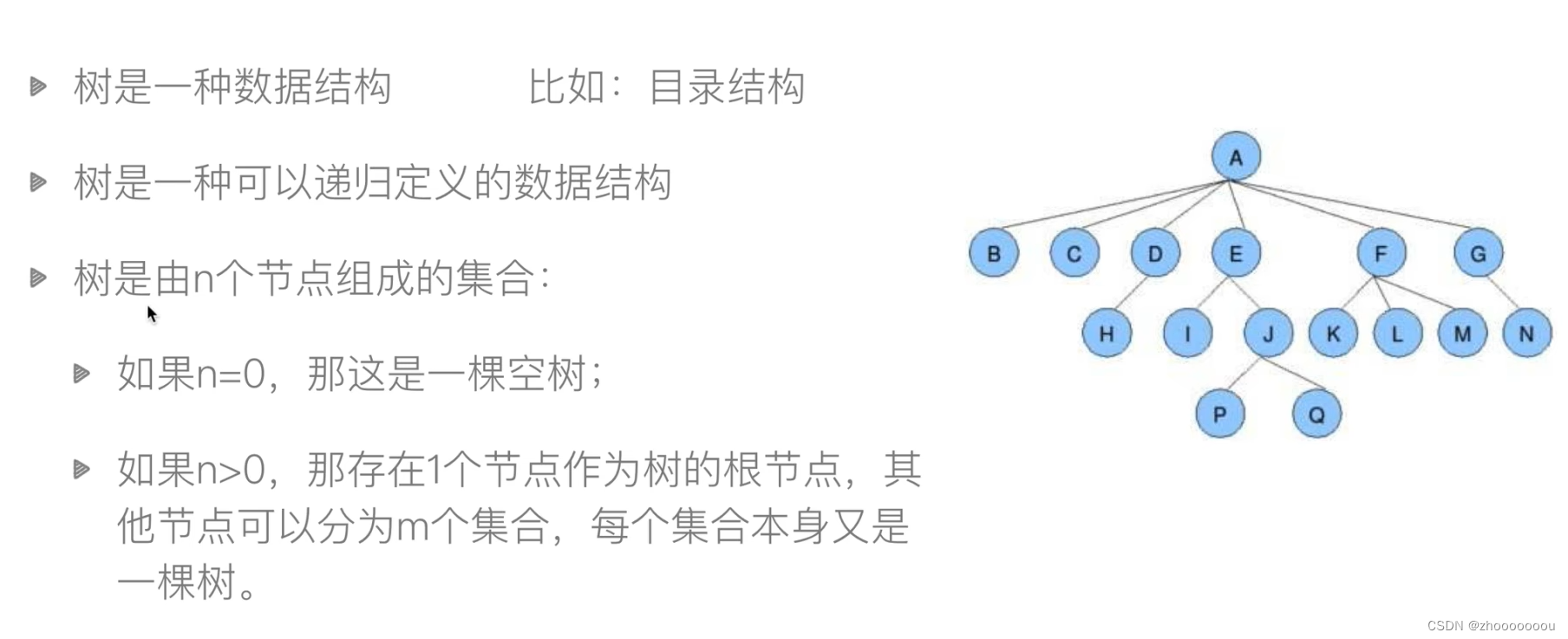
一些基本知识:
根节点:每棵树最上面的单独的一个节点,如上图A为根节点。
叶子节点:每棵树中最末梢的,不再有分支的节点。如上图B,C,H,I,P,Q,K,L,M,N为叶子节点。
树的深度(高度):层数是几,深度(高度)是几。如上图树的深度(高度)是4,因为有4层。
节点的度:某个分叉的节点分了几个叉,节点的度就是几。如上图E的度为2,F的度为3.
树的度: 节点的度中最大的数,就是树的度。如上图节点的度最大为A分了6个叉,所以树的度为6
孩子节点/父节点:挂在某个节点下面,称为这个节点的孩子节点,某个节点称为父节点。如上图中E是父节点,I,J是孩子节点。
子树:在树中单独拎出来一些节点还能组成树的,称为这棵树的子树。如上图中E,F,G单独拎出来后还是一棵树,故能称为是A这棵树的子树。
这些都是按照我理解的概念写出来的,可能不完善也不是很清楚,最好还是参考课本上的定义概念。
二叉树

满二叉树、完全二叉树
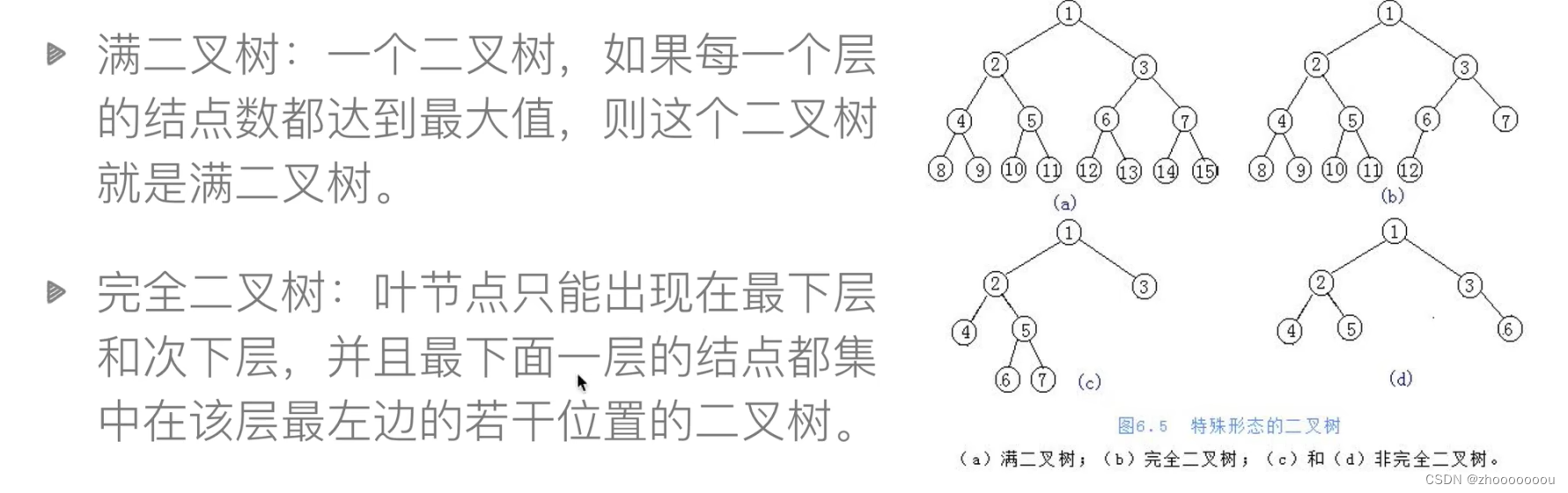
完全二叉树:最下一层可以不满,但节点序号必须按照从左到右排序的方式进行排列
二叉树的存储方式
因为堆排序要用到二叉树的存储方式,所以要了解一下

在堆排序中我们使用顺序存储方式,那么就是把数字放到列表中,在下图中找到父节点与左孩子和右孩子节点之间的数字关系,以方便我们去寻找数据。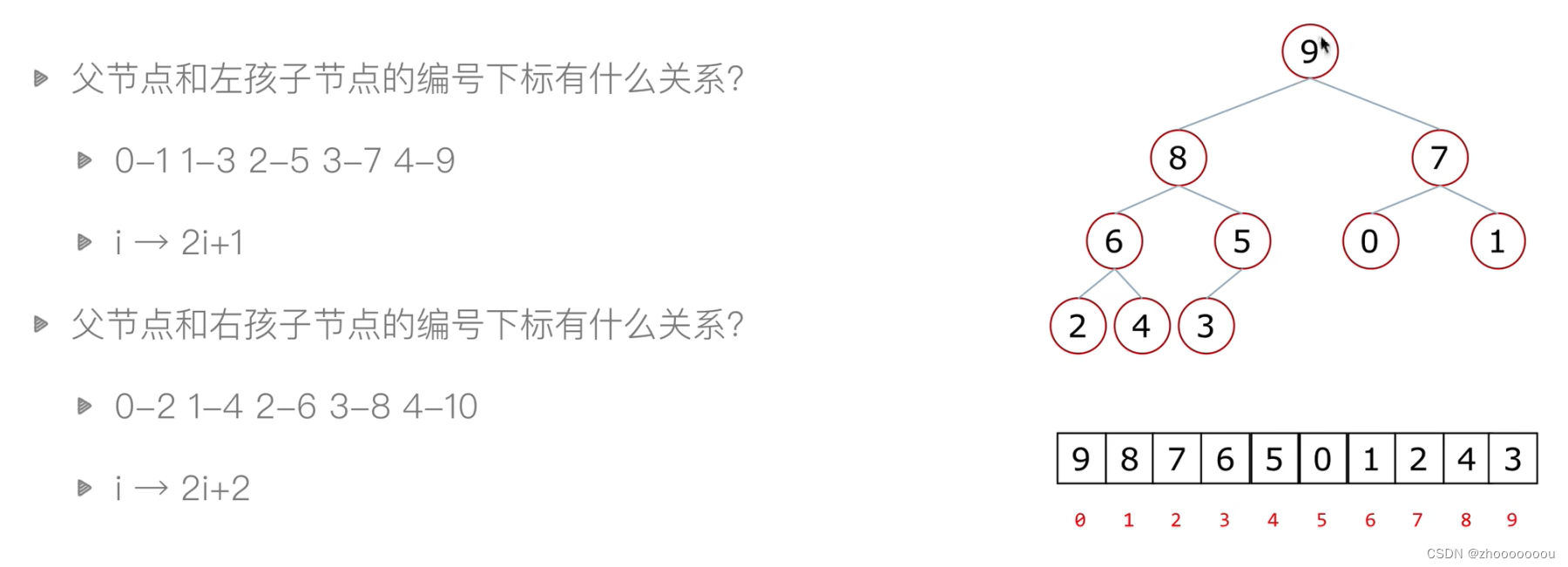
堆排序 - 什么是堆

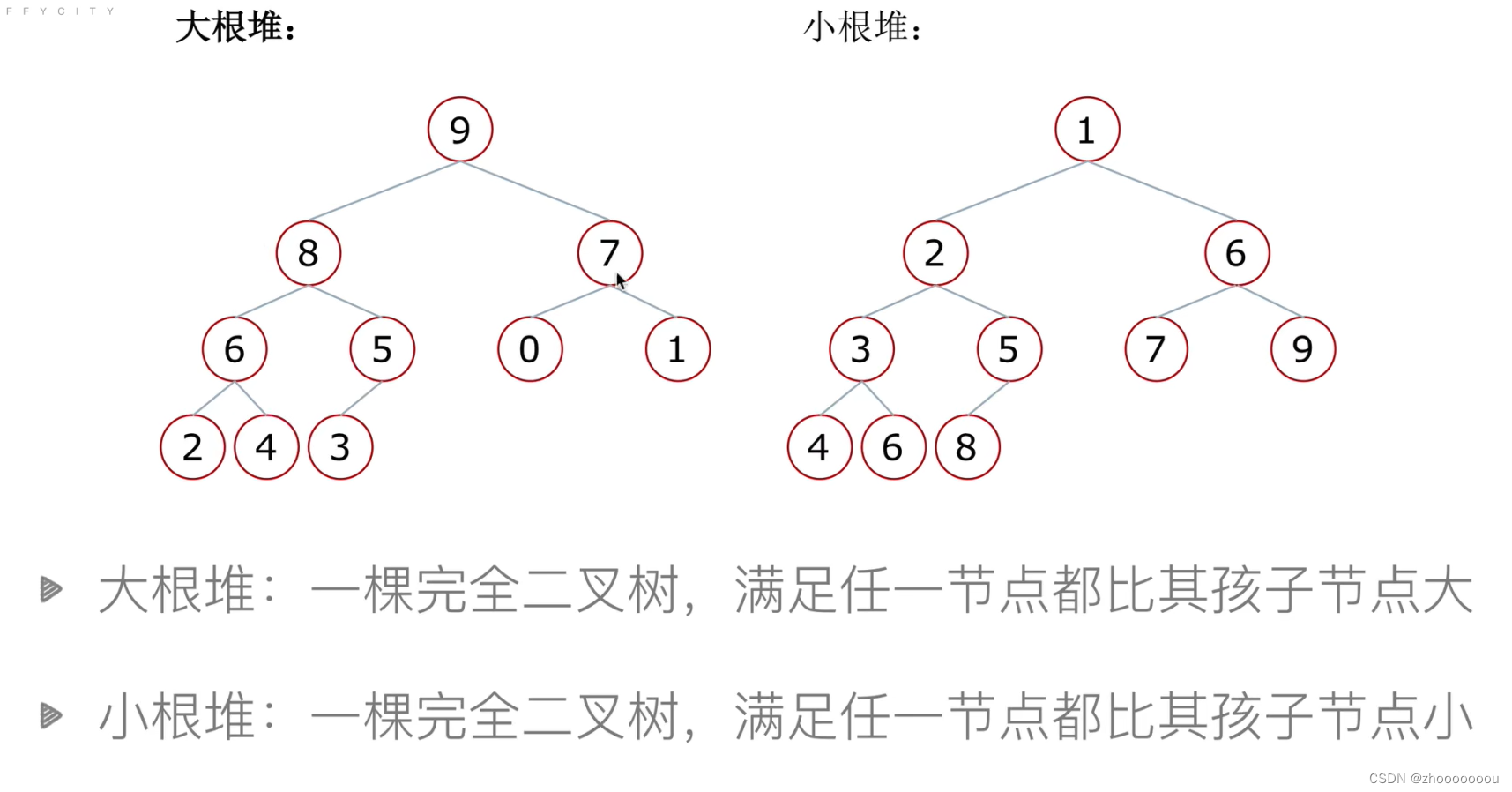
堆的向下调整
节点的左右子树都是堆,但自身不是堆,可以通过一次次的向下调整来将其变成一个堆。
堆排序的过程

ok代码实现问题明日再学习。
三、学习碎碎念
慢慢开始上难度了,今天上算法课回答问题了,根据之前自己的冒泡排序的笔记,果然是一份耕耘一份收获啊。也想对自己说别太浮躁,别太着急,慢慢来,一步一个脚印,踏踏实实的,努力的去迎接自己的未来。
这篇关于备战蓝桥杯Day19 - 堆排序基础知识的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







