【N皇后问题】【leetcode51】（Java）

本文主要是介绍【N皇后问题】【leetcode51】（Java），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【N皇后问题】【leetcode51】

问题描述

八皇后问题，一个古老而著名的问题，是回溯算法的典型案例。该问题由国际西洋棋棋手马克斯·贝瑟尔于 1848 年提出：在 8×8 格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。高斯认为有 76 种方案。1854 年在柏林的象棋杂志上不同的作者发表了 40 种不同的解，后来有人用图论的方法解出 92 种结果。计算机发明后，有多种计算机语言可以编程解决此问题。
在这里插入图片描述

输出结果要求

输入: 4
输出: [[".Q..",  // 解法 1"...Q","Q...","..Q."],["..Q.",  // 解法 2"Q...","...Q",".Q.."]
]

解题思路

针对N皇后问题，若要求解出所有可能的解，这必须列举出N个皇后位置所有的可能组合。一种求解方式就是把N个皇后在棋盘中的所有位置的组合都列举出来，然后依次判断每一个组合会不会出现攻击。这种方法的时间复杂度 O(N^N)，显然复杂度是相当高的。
为了能够简化时间复杂度，我们在按照一行一行的当时去放置N个皇后，每行都会放置一个皇后，并且该行放置皇后的位置最大为N；一旦本行的皇后确定了位置后，那么她所在的行(row)，列(col)，左斜(hill)，右斜(dale) 都不能再放皇后，这样，考虑下一行的皇后的位置时可能的位置就必须避开这些位置。
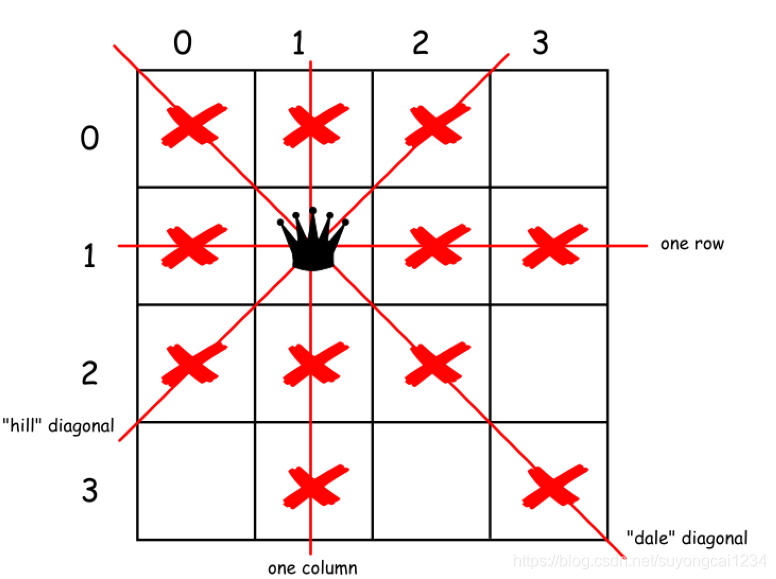
在这里插入图片描述
对于第一行，有N个位置可以放置皇后；
对于第二行，有N - 3个位置可以放置皇后；

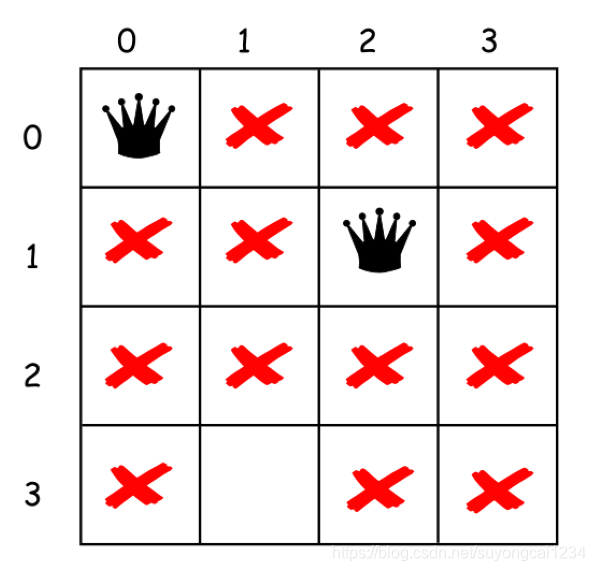
因此，我们一行一行的放置皇后的位置，如果发现该行没有可以放置皇后的位置时，则回溯到上一行重新放置上一行的皇后的位置。这就是回溯算法。
实现
观察棋盘，一共有 N 个row， N 个col，2N - 1 个hill，2N - 1 个dale。因此，为了能够记录哪一行、列、斜不能放置皇后，引入数组记录：

	int n;int[] rows; // 所在行是否有queenint[] hills;  // 左斜是否有queenint[] dales;  // 右斜是否有queenint[] queens; // 每列queen 放置的位置

判断该位置是否能放置皇后

    private boolean isAttack(int row, int col){int res = rows[col] + hills[row - col + 2 * n] + dales[row + col];return res == 0;}

放置皇后，在位置（row，col）放置皇后后，需更新 rows, hill, dales数组

    private void placeQueen(int row, int col){queens[row] = col;rows[col] =  1;hills[row - col + 2 * n] = 1;dales[col + row] = 1;}

移走皇后，在位置（row，col）移走皇后后，需更新 rows, hill, dales数组

    private void removeQueen(int row, int col){queens[row] = 0;rows[col] = 0;hills[row - col + 2 * n] = 0;dales[col + row] = 0;}

所有位置都放置好后，生成所需要的字符串列表

    private void addSolution(){List<String> solution = new ArrayList<>();for(int i = 0; i < n; i ++){int col = queens[i];StringBuilder sb = new StringBuilder();for(int j = 0; j < col; j ++)sb.append(".");sb.append("Q");for(int j = col + 1; j < n; j ++)sb.append(".");solution.add(sb.toString());}output.add(solution);}

核心回溯算法

    private void backtrace(int row){for(int col = 0; col < n; col ++){if(isAttack(row, col)){placeQueen(row, col);if(row == n - 1)addSolution();elsebacktrace(row + 1);removeQueen(row, col);}}}

整体代码

class Solution {int[] rows; // 所在行是否有queenint[] hills;  // 左斜是否有queenint[] dales;  // 右斜是否有queenint n;int[] queens; // 每列queen 放置的位置List<List<String>> output;public List<List<String>> solveNQueens(int n){this.n = n;rows = new int[n];hills = new int[4*n - 1];dales = new int[2*n - 1];queens = new int[n];output = new ArrayList<>();backtrace(0);return output;}private boolean isAttack(int row, int col){int res = rows[col] + hills[row - col + 2 * n] + dales[row + col];return res == 0;}private void placeQueen(int row, int col){queens[row] = col;rows[col] =  1;hills[row - col + 2 * n] = 1;dales[col + row] = 1;}private void removeQueen(int row, int col){queens[row] = 0;rows[col] = 0;hills[row - col + 2 * n] = 0;dales[col + row] = 0;}private void addSolution(){List<String> solution = new ArrayList<>();for(int i = 0; i < n; i ++){int col = queens[i];StringBuilder sb = new StringBuilder();for(int j = 0; j < col; j ++)sb.append(".");sb.append("Q");for(int j = col + 1; j < n; j ++)sb.append(".");solution.add(sb.toString());}output.add(solution);}private void backtrace(int row){for(int col = 0; col < n; col ++){if(isAttack(row, col)){placeQueen(row, col);if(row == n - 1)addSolution();elsebacktrace(row + 1);removeQueen(row, col);}}}
}