本文主要是介绍推荐系统论文粗读记录【一】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.【FM】《Factorization Machines》
作者: Rendle, Steffen
发布时间: 2010-12
来源: 2010 IEEE International Conference on Data Mining
引用数: 2062
地址: https://doi.org/10.1109/ICDM.2010.127
笔记: FM将SVM模型的优势和因式分解模型结合。FM模型的优势:1、允许在数据稀疏的情况下参数估计。2、FM模型复杂度是线性的,3、FM模型是通用的预测模型,可以应用于任何实值向量。
FM模型被定义为: y ^ ( x ) : = w 0 + ∑ i = 1 n w i x i + ∑ i = 1 n ∑ j = i + 1 n < v i , v j > x i x j \hat y(\mathbf x):=w_0+\sum_{i=1}^{n}w_ix_i+\sum_{i=1}^{n}\sum_{j=i+1}^{n}<\mathbf v_i,\mathbf v_j>x_ix_j y^(x):=w0+i=1∑nwixi+i=1∑nj=i+1∑n<vi,vj>xixj其中 < v i , v j > : = ∑ f = 1 k v i , f ⋅ v j , f <\mathbf v_i,\mathbf v_j>:=\sum\limits_{f=1}^{k}v_{i,f}·v_{j,f} <vi,vj>:=f=1∑kvi,f⋅vj,f, k k k是定义的因子分解的维度,是一个超参数。模型的时间复杂度为 O ( k n 2 ) O(kn^2) O(kn2) 。通过数学转换变成线性复杂度 O ( k n ) O(kn) O(kn) ∑ i = 1 n ∑ j = i + 1 n < v i , v j > x i x j \sum_{i=1}^{n}\sum_{j=i+1}^{n}<\mathbf v_i,\mathbf v_j>x_ix_j\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space i=1∑nj=i+1∑n<vi,vj>xixj = 1 2 ∑ i = 1 n ∑ j = 1 n < v i , v j > x i x j − 1 2 ∑ i = 1 n < v i , v i > x i x i =\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}<\mathbf v_i,\mathbf v_j>x_ix_j-\frac{1}{2}\sum_{i=1}^{n}<\mathbf v_i,\mathbf v_i>x_ix_i\space\space\space\space\space\space\space\space =21i=1∑nj=1∑n<vi,vj>xixj−21i=1∑n<vi,vi>xixi = 1 2 ( ∑ i = 1 n ∑ j = 1 n ∑ f = 1 k v i , f v j , f x i x j − ∑ i = 1 n ∑ f = 1 k v i , f v i , f x i x i ) =\frac{1}{2}(\sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{f=1}^{k}v_{i,f}v_{j,f}x_ix_j-\sum_{i=1}^{n}\sum_{f=1}^{k}v_{i,f}v_{i,f}x_ix_i)\space\space\space\space\space\space\space\space\space\space\space\space =21(i=1∑nj=1∑nf=1∑kvi,fvj,fxixj−i=1∑nf=1∑kvi,fvi,fxixi) = 1 2 ∑ f = 1 k ( ( ∑ i = 1 n v i , f x i ) ( ∑ j = 1 n v j , f x j ) − ∑ i = 1 n v i , f 2 x i 2 ) =\frac{1}{2}\sum_{f=1}^{k}((\sum_{i=1}^{n}v_{i,f}x_i)(\sum_{j=1}^{n}v_{j,f}x_j)-\sum_{i=1}^{n}v_{i,f}^2x_i^2)\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space =21f=1∑k((i=1∑nvi,fxi)(j=1∑nvj,fxj)−i=1∑nvi,f2xi2) = 1 2 ∑ f = 1 k ( ( ∑ i = 1 n v i , f x i ) 2 − ∑ i = 1 n v i , f 2 x i 2 ) =\frac{1}{2}\sum_{f=1}^{k}((\sum_{i=1}^{n}v_{i,f}x_i)^2-\sum_{i=1}^{n}v_{i,f}^2x_i^2)\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space =21f=1∑k((i=1∑nvi,fxi)2−i=1∑nvi,f2xi2)
2.【FFM】《Field-aware Factorization Machines for CTR Prediction》
作者: Juan, Yuchin and Zhuang, Yong and Chin, Wei-Sheng and Lin, Chih-Jen
发布时间: 2016-09
来源: Association for Computing Machinery Proceedings of the 10th ACM Conference on Recommender Systems
引用数: 273
地址: https://doi.org/10.1145/2959100.2959134
笔记: FFM模型的想法来源于【PITF模型】,加入了Field信息,之前的FM模型每个特征只有一个语义向量,FFM模型每个特征有多个语义向量对于不同的field。 Φ F F M ( ( w , v ) , x ) = w 0 + ∑ i = 1 m x i w i + ∑ i = 1 m ∑ j = i + 1 m x i x j < v i , F ( j ) , v j , F ( i ) > \Phi_{FFM}((w,v),x)=w_0+\sum_{i=1}^{m}x_iw_i+\sum_{i=1}^{m}\sum_{j=i+1}^{m}x_ix_j<v_{i,F(j)},v_{j,F(i)}> ΦFFM((w,v),x)=w0+i=1∑mxiwi+i=1∑mj=i+1∑mxixj<vi,F(j),vj,F(i)>相对于FM模型就是对后面的特征交互项进行了改进。
3.【FwFM】《Field-weighted Factorization Machines for Click-Through Rate Prediction in Display Advertising》
作者: Pan, Junwei and Xu, Jian and Ruiz, Alfonso Lobos and Zhao, Wenliang and Pan, Shengjun and Sun, Yu and Lu, Quan
发布时间: 2018-03
来源: Proceedings of the 2018 World Wide Web Conference on World Wide Web
引用数: 114
地址: https://arxiv.org/abs/1806.03514
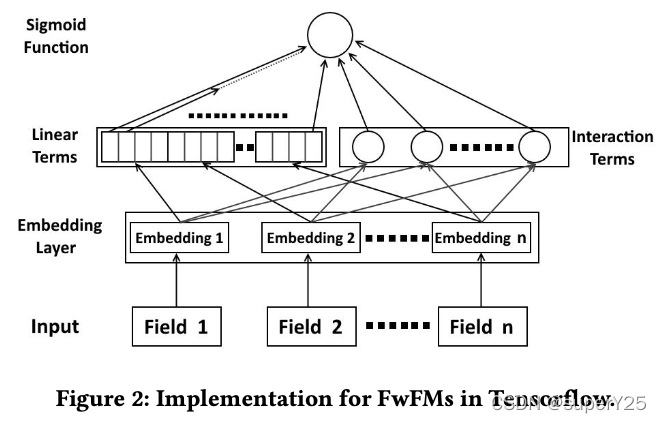
笔记: FwFM模型在不同的field之间构建不同的特征交互。多类别特征数据的几个挑战:1、特征交互时普遍的,需要专门建模。2、不同field的不同特征交互是不同的。3、潜在的高模型复杂度。FwFM模型: Φ F w F M s ( ( w , v ) , x ) = w 0 + ∑ i = 1 m x i w i + ∑ i = 1 m ∑ j = i + 1 m x i x j < v i , v j > r F ( i ) , F ( j ) \Phi_{FwFMs}((w,v),x)=w_0+\sum_{i=1}^{m}x_iw_i+\sum_{i=1}^{m}\sum_{j=i+1}^{m}x_ix_j<v_i,v_j>r_{F(i),F(j)} ΦFwFMs((w,v),x)=w0+i=1∑mxiwi+i=1∑mj=i+1∑mxixj<vi,vj>rF(i),F(j)模型参数对比:
模型的TensorFlow实现:
4.【FmFM】《FM2: Field-Matrixed Factorization Machines for Recommender Systems》
作者: Sun, Yang and Pan, Junwei and Zhang, Alex and Flores, Aaron
发布时间: 2021-06
来源: Association for Computing Machinery Proceedings of the Web Conference 2021
引用数: 9
地址: https://doi.org/10.1145/3442381.3449930
笔记: 数据:多领域类别数据,每个特征属于一个领域。本文提出一个新颖的,高校准确地构建领域信息模型的方法。该方法是直接在FwFM的基础上进行改进。微调了交叉项,支持指定领域类型可变维度向量输入。论文对之前的一系列FM模型进行了分析:
1、最初的线性模型缺乏对特征交互的表示。
2、改进线性模型,增加特征之间的交互项,使用二次多项式模型。模型参数太多O(m^2)
3、使用FM替换二次多项式,使用特征向量的点积表示特征之间的交互信息。FM忽略了一个特征和不同类别中的特征之间的交互具有不同的行为结果。
4、FFM(Field-aware FM)为特征向量增加field类别信息F(i)。大量的参数使得模型在实际生产中不可用。
5、FwFM(Field-weighted FM)为特征之间不同领域增加权重。
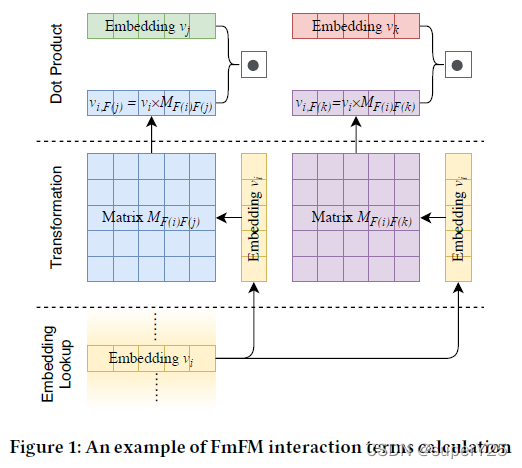
FmFM(Field-matrix FM)通过二维矩阵表示两个领域类别的交互信息,把模型进行拆分三个步骤:1、feature embedding lookup;2、特征(i)和领域类别矩阵(M)交互的Transformation。3、特征(j)和步骤2的结果进行dot-product。 Φ F m F M ( ( w , v ) , x ) = w 0 + ∑ i = 1 m x i w i + ∑ i = 1 m ∑ j = i + 1 m x i x j < v i M F ( i ) , F ( j ) , v j > \Phi_{FmFM}((w,v),x)=w_0+\sum_{i=1}^{m}x_iw_i+\sum_{i=1}^{m}\sum_{j=i+1}^{m}x_ix_j<v_iM_{F(i),F(j)},v_j> ΦFmFM((w,v),x)=w0+i=1∑mxiwi+i=1∑mj=i+1∑mxixj<viMF(i),F(j),vj>
5.【TransFM】《Translation-Based Factorization Machines for Sequential Recommendation》
作者: Pasricha, Rajiv and McAuley, Julian
发布时间: 2018-09
来源: Association for Computing Machinery Proceedings of the 12th ACM Conference on Recommender Systems
引用数: 28
地址: https://doi.org/10.1145/3240323.3240356
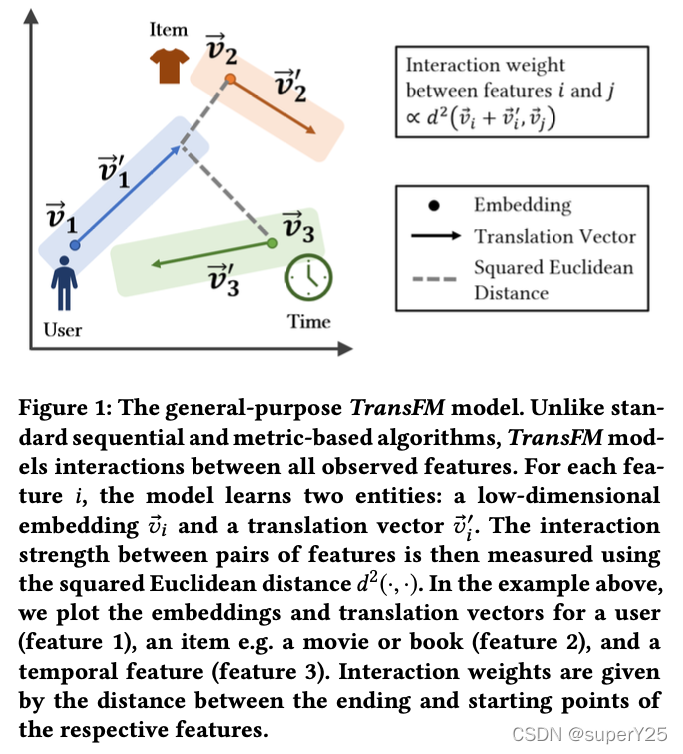
笔记: 通过用户历史上的一系列行为预测未来的行为,从而进行推荐。TransFM模型将转换算法和基于FM的序列推荐算法结合起来。利用translation component 替代FM特征交互的内积,并使用平方欧式距离来比较特征维数对之间的兼容性(如下图)。
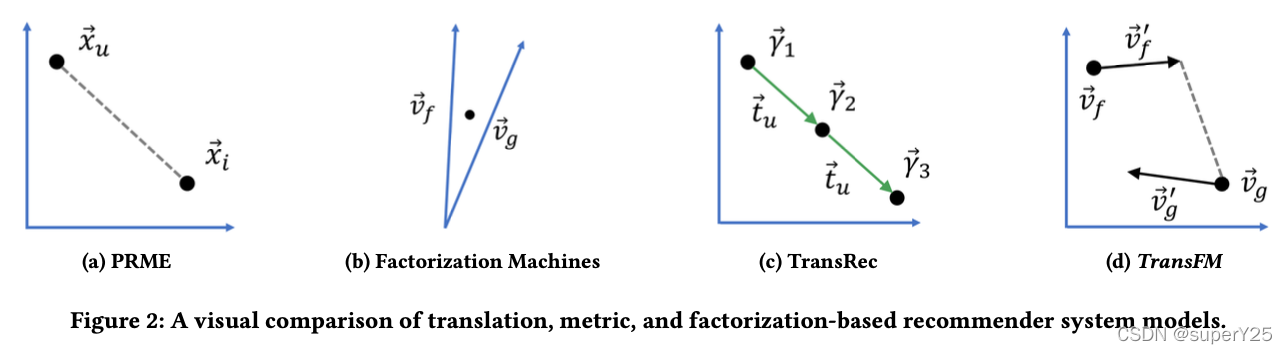
模型被定义为: y ^ ( x ⃗ ) = w 0 + ∑ i = 1 n w i x i + ∑ i = 1 n ∑ j = i + 1 n d 2 ( v ⃗ i + v ⃗ i ′ , v ⃗ j ) x i x j \hat y(\vec x)=w_0+\sum_{i=1}^{n}w_ix_i+\sum_{i=1}^{n}\sum_{j=i+1}^{n}d^2(\vec v_i+\vec v'_i,\vec v_j)x_ix_j y^(x)=w0+i=1∑nwixi+i=1∑nj=i+1∑nd2(vi+vi′,vj)xixj其中平方欧式距离: d 2 ( a ⃗ , b ⃗ ) = ( a ⃗ − b ⃗ ) ⋅ ( a ⃗ − b ⃗ ) = ∑ f = 1 k ( a f − b f ) 2 d^2(\vec a,\vec b)=(\vec a-\vec b)·(\vec a-\vec b)=\sum\limits_{f=1}^{k}(a_f-b_f)^2 d2(a,b)=(a−b)⋅(a−b)=f=1∑k(af−bf)2下图提供了TransFM使用的预测方法和各种基线模型的比较:
这篇关于推荐系统论文粗读记录【一】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!