深度学习之图像分割（三）—— 空洞卷积/膨胀卷积（霹雳吧啦wz）

引入空洞卷积

1.空洞卷积的优缺点：

1.空洞卷积的优点

1.增大感受野：传统的下采样虽可增加感受野，但会降低空间分辨率。而使用空洞卷积能够在扩大感受野的同时，保证分辨率。这十分适用于检测、分割任务中，感受野的增大可检测、分割大的目标，高分辨率则可精确定位目标。
2.保持原输入特征图W、H（一般通过padding）
3.捕获多尺度上下文信息：空洞卷积中参数 dilation rate 表明在卷积核中填充 (dilation rate-1) 个 0。设置不同 dilation rate 给网络带来不同的感受野，即获取了多尺度信息。

2.空洞卷积的缺点

1.局部信息丢失：由于空洞卷积的计算方式类似于棋盘格式，某一层得到的卷积结果，来自上一层的独立的集合，没有相互依赖，因此该层的卷积结果之间没有相关性，即局部信息丢失；
2.远距离获取的信息没有相关性：由于空洞卷积稀疏的采样输入信号，使得远距离卷积得到的信息之间没有相关性。

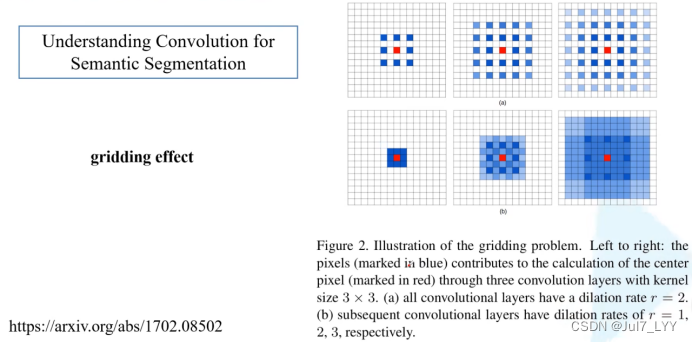
2.Gridding effect:网格影响

Gridding effect：没有用到范围内的所有像素值，而只使用到了一部分。非零元素中间有0元素（没有使用到的元素），因此一定会失去一部分信息。

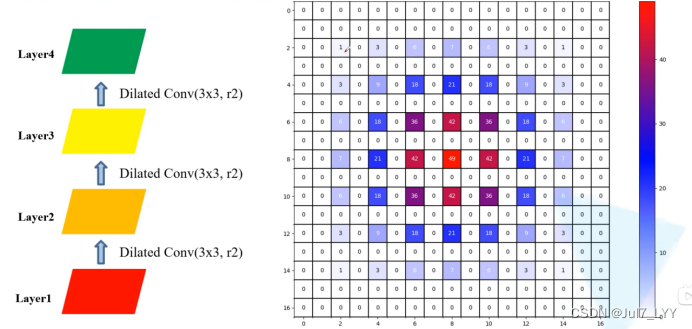
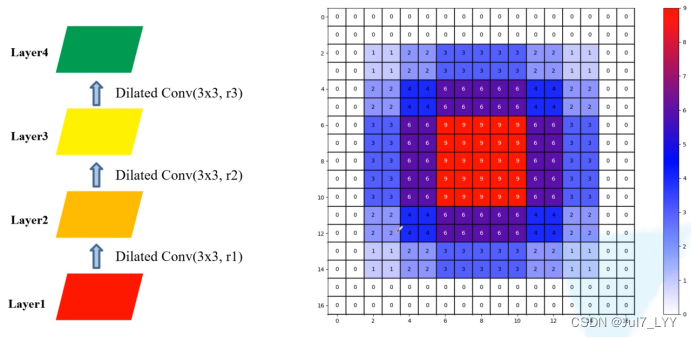
3.解决办法：Hybrid Dilated Convolution（HDC）

连续使用膨胀卷积时，膨胀系数不同。感受野13*13

对比普通卷积，可以看到感受野明显减小了很多，感受野7*7

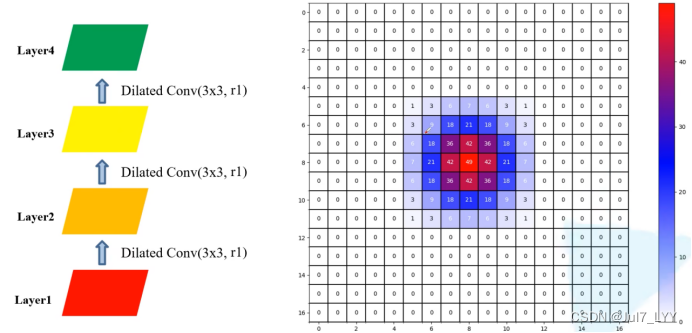
4.在连续使用多个膨胀卷积时，该如何设置膨胀系数？

方法1.使用公式验证膨胀系数的大小

Mi就等于第i层两个非零元素之间的距离，ri就等于第i层的膨胀系数。我们的目标是M2≤K。根据三个膨胀系数，计算值是否合适。

方法2.将膨胀系数设置成锯齿结构

方法3.膨胀系数的公约数不能大于1

5.对比实验

第二行是没有使用HDC方法，第三行是使用了HDC

6.反卷积计算公式

假设输入特征图的尺寸为 $H_{in}\times W_{in}\times C_{in}$，输出特征图的尺寸为 $H_{out}\times W_{out}\times C_{out}$，上采样倍数为 $k$，膨胀卷积核大小为 $k_h\times k_w$，填充大小为 $p_h\times p_w$，跨度为 $s_h\times s_w$，则膨胀卷积的系数计算如下：

计算输出特征图的尺寸：
$$H_{out}=(H_{in}-1)\times s_h+k_h-2\times p_h$$

$$W_{out}=(W_{in}-1)\times s_w+k_w-2\times p_w$$