机器学习----SVM（2）从原始问题到对偶问题的转换

本文主要是介绍机器学习----SVM（2）从原始问题到对偶问题的转换，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

SVM的水真是太深了，只能一点一点的解决了，今天这篇博客简单讲解SVM的目标函数从原始问题到对偶问题的转换。在这里再给大家一个大牛的博客链接：http://blog.pluskid.org/?p=685

1、转化对偶问题

上篇博客中我们得到的目标函数：

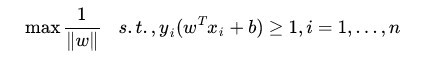（1）

我们在优化时喜欢求最小值，将上式转化正等价的求最小值如下：

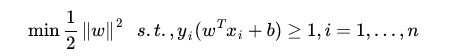      （2）

对于（2）式，这是一个凸二次规划问题，我们可以使用拉格朗日乘数法进行优化。    

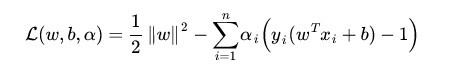    （3）

（3）式中的是拉格朗日乘子，然后我们令：        

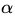
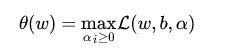            （4）

为什么能这样假设呢？如果约束条件都满足，（4）式的最优值就是，和目标函数一样。

因此我们可以直接求（4）式的最小值，等价于求原目标函数。因此目标函数变成如下：

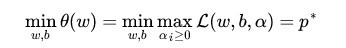（5）

将求最大值和最小值交换位置后

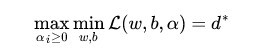（6）

交换以后的新问题是原始问题的对偶问题，这个新问题的最优值用来表示。而且有d*≤p*，在满足某些条件的情况下，这两者相等，这个时候就可以通过求解对偶问题来间接地求解原始问题。为什么要这样转换呢？此处借他人之言，之所以从minmax的原始问题，转化为maxmin的对偶问题，一者因为是的近似解，二者，转化为对偶问题后，更容易求解。下面可以先求L 对w、b的极小，再求L 对的极大。

2、求解对偶问题

回顾一下上面的目标函数L

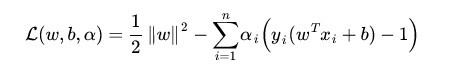（7）

这是一个拉格朗日乘法优化方法得到的，由于要求

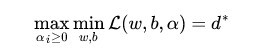（8）

先求最大值，后求最小值，求最小值时，将a看成常量，那么L就是w,b的函数了。极值在导数为0的点处取到，因此分
别求L对w,b的导数，并令其为0，得如下结果。

（9）

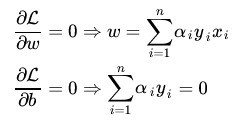
将（9）式带入（7）（为什么呢？）得到：

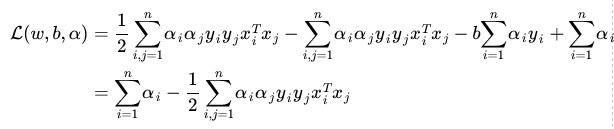（10）

为什么能将（9）式带入（7）式呢？因为极值在导数为零的点处取到，因此（9）式符合（7）式取极值时w,b的取值。（10）式就是（7）式的最小值了，求完最小值，然后求最大值。求对的极大，即是关于对偶问题的最优化问题。经过上面第一个步骤的求w和b，得到的拉格朗日函数式子已经没有了变量w，b，只有。从上面的式子得到：

（11）

（11）式是关于a的式子，如果能求出a，则可以根据(7)式求出w。求出w后可以根据前面函数距离等于1的假设求出b

怎样求a呢？这需要后面的核函数和松弛量的知识，利用SMO算法求解，下篇博客继续介绍核函数。
最后给大家附一张我的推到图，是上面内容的简化版本。

这篇关于机器学习----SVM（2）从原始问题到对偶问题的转换的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---