本文主要是介绍随机过程初级教程 第一章,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
随机过程初级教程 第一章
- 概率公式
- 全概率公式
- 随机变量的无限族
- 特征函数
- 母函数和拉普拉斯变换
- 一些常见的分布
- 极限定理
- 不等式
- 随机过程的例子
- 布朗运动
- 泊松过程
- 随机过程类型
- 平稳独立增量过程
- 鞅
- 马尔科夫过程
- 平稳过程
- 更新过程
- 点过程
概率公式
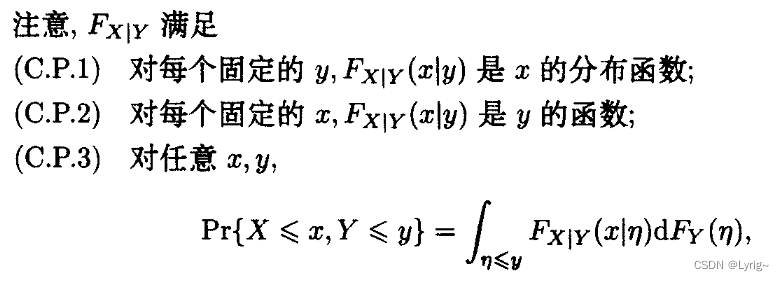

全概率公式
P r ( X ≤ x ) = P r ( X ≤ x , Y ≤ ∞ ) = ∫ − ∞ + ∞ F X ∣ Y ( x ∣ y ) d F Y ( y ) Pr(X\leq x)=Pr(X\leq x, Y\leq \infty)=\int_{-\infty}^{+\infty}{F_{X|Y}(x|y)dF_Y(y)} Pr(X≤x)=Pr(X≤x,Y≤∞)=∫−∞+∞FX∣Y(x∣y)dFY(y)
当 Y Y Y有概率密度函数 p Y ( y ) p_Y(y) pY(y)时,公式转变为:
P r ( X ≤ x ) = P r ( X ≤ x , Y ≤ ∞ ) = ∫ − ∞ + ∞ P r ( X ≤ x ∣ Y = y ) p Y ( y ) d y Pr(X\leq x)=Pr(X\leq x, Y\leq \infty)=\int_{-\infty}^{+\infty}{Pr(X\leq x|Y=y)p_Y(y)dy} Pr(X≤x)=Pr(X≤x,Y≤∞)=∫−∞+∞Pr(X≤x∣Y=y)pY(y)dy
当 x , y x,y x,y有联合密度时,我们可以定义 Y = y Y=y Y=y时,X的条件密度函数为 p X ∣ Y ( x ∣ y ) = d d x F X ∣ Y ( x ∣ y ) = p X Y ( x y ) p Y ( y ) p_{X|Y}(x|y)=\frac{d}{dx}F_{X|Y}(x|y)=\frac{p_{XY}(xy)}{p_Y(y)} pX∣Y(x∣y)=dxdFX∣Y(x∣y)=pY(y)pXY(xy)


随机变量的无限族

特征函数



母函数和拉普拉斯变换


一些常见的分布






极限定理






不等式


随机过程的例子

布朗运动


泊松过程

随机过程类型
平稳独立增量过程
独立增量: X t − X t − 1 , ∀ t ∈ T X_t-X_{t-1}, \forall t\in T Xt−Xt−1,∀t∈T互相独立。
平稳增量: X t − X s , t > s X_t-X_s, t>s Xt−Xs,t>s只与 t − s t-s t−s有关,与 s s s无关。
鞅
∀ t 1 , t 2 , . . . , t n , a n d ∀ a 1 , a 2 , . . . , a n ∈ R E [ X t n + 1 ∣ X 1 = a 1 , X 2 = a 2 , . . . , X t n = a n ] = a n \forall t_1,t_2,...,t_n, and \forall a_1,a_2,...,a_n\in R\\ E[X_{t_n+1}|X_1=a_1,X_2=a_2,...,X_{t_n}=a_n]=a_n ∀t1,t2,...,tn,and∀a1,a2,...,an∈RE[Xtn+1∣X1=a1,X2=a2,...,Xtn=an]=an
马尔科夫过程
∀ t 1 , t 2 , . . . , t n < t P r ( a < X t < b ∣ X 1 = x 1 , X 2 = x 2 , . . . , X t n = x n ) = P r ( a < X t < b ∣ X t n = x n ) \forall t_1,t_2,...,t_n<t\\ Pr(a<X_t<b|X_1=x_1,X_2=x_2,...,X_{t_n}=x_n)=Pr(a<X_t<b|X_{t_n}=x_n) ∀t1,t2,...,tn<tPr(a<Xt<b∣X1=x1,X2=x2,...,Xtn=xn)=Pr(a<Xt<b∣Xtn=xn)
这蕴含着条件独立性。
转移概率函数: p ( x , s ; t , A ) = P r ( X t ∈ A ∣ X s = x ) p(x,s;t,A)=Pr(X_t\in A|X_s=x) p(x,s;t,A)=Pr(Xt∈A∣Xs=x)
马尔科夫链:状态空间是有限或可数的马尔可夫过程。
扩散过程:状态空间是连续的马尔可夫过程。
平稳过程
严格平稳:对任意 h > 0 h>0 h>0和任意 t 1 , t 2 , . . . , t n ∈ T t_1,t_2,...,t_n\in T t1,t2,...,tn∈T,随机变量组 ( X t 1 + h , X t 2 + h , . . . , X t n + h ) (X_{t_1+h},X_{t_2+h},...,X_{t_n+h}) (Xt1+h,Xt2+h,...,Xtn+h)和 ( X t 1 , X t 2 , . . . , X t n ) (X_{t_1},X_{t_2},...,X_{t_n}) (Xt1,Xt2,...,Xtn)的联合分布函数相同。
特别的对任意时刻t, X t X_t Xt的分布都相同。
称马尔可夫过程有平稳转移概率,如果 p ( x , s ; t , A ) p(x,s;t,A) p(x,s;t,A)是 t − s t-s t−s的函数。
泊松过程和布朗运动都不是平稳的,但增量 Z t = X t + h − X t Zt = X_{t+h} − X_t Zt=Xt+h−Xt对任意固定h是平稳随机过程
不存在非常数的平稳独立增量过程是平稳过程。
更新过程

点过程

这篇关于随机过程初级教程 第一章的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








