【优化数学模型】2. 动态规划DP方法的求解思路

本文主要是介绍【优化数学模型】2. 动态规划DP方法的求解思路，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在这里插入图片描述

【优化数学模型】2. 动态规划DP方法的求解思路

一、动态规划
- 1. 概述
- 2. 最优性原理
- 3. 最优子结构特性
二、示例：0-1背包问题
- 1. 问题描述
- 2. 使用自顶向下的方法
- 3. 使用自下而上的方法

一、动态规划

1. 概述

多阶段决策问题，就是要在允许的决策范围内，选择一个最优决策使整个系统在预定标准下达到最佳效果。

动态规划 (dynamic programming,DP) 是用来解决多阶段决策过程最优化的一种数量方法。其特点在于，它可以把一个n维决策问题变换为几个一维最优化问题，从而一个一个地去解决。

与分而治之技术的不同之处在于，动态规划解决方案中的子问题是重叠的，因此解决一个子问题所需的一些相同步骤也需要用于其他子问题。

许多文章中提到动态规划会将其称为是一种经典的算法，需要指出的是，动态规划是1951年，美国数学家贝尔曼等人根据一类多阶段决策问题特性提出的解决这类问题的“最优化原理”，是其创建出的最优化问题的一种新思路，是求解一类问题的一种方法，是考察问题的一种途径，而不是一种算法。

在解决相应问题时，必须对具体问题进行具体分析，运用动态规划的原理和方法，建立相应的模型，然后再用动态规划方法去求解。

在这里插入图片描述

2. 最优性原理

应用动态规划设计使多阶段决策过程达到最优（成本最省、效益最高、路径最短等），依据动态规划的最优性原理：“作为整个过程的最优策略具有这样的性质，无论过去的状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略”。也就是说，最优决策序列中的任何子序列都是最优的。

3. 最优子结构特性

最优性原理体现为问题的最优子结构特性。当一个问题的最优解中包含了子问题的最优解时，则称该问题具有最优子结构特性。最优子结构特性使得在从较小问题的解构造较大问题的解时，只需考虑子问题的最优解，从而大大减少了求解问题的计算量。

二、示例：0-1背包问题

1. 问题描述

0-1背包问题是应用动态规划设计求解的典型案例。

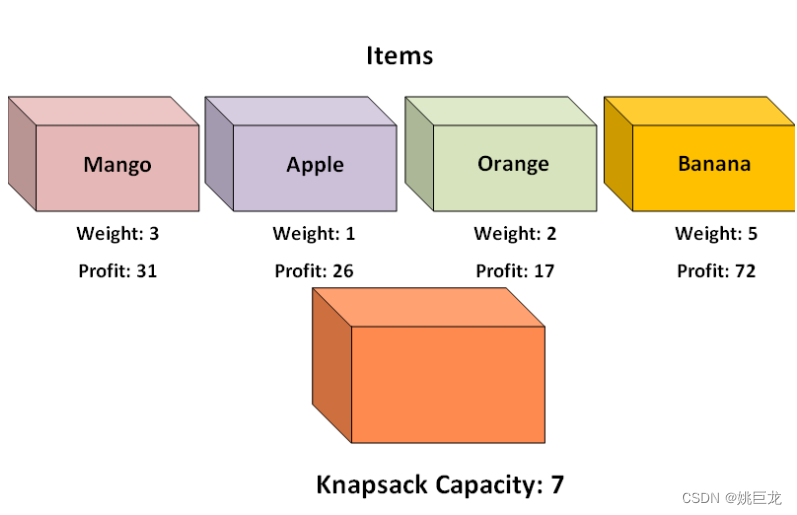
已知有 N 种物品和一个可容纳 W 重量的背包，物品 i 的重量为 $w_i$ ，产生的效益为 $p_i$ 。在装包时物品 i 可以装入，也可以不装，但不可拆开装。即物品 i可产生的效益为 $x_ip_i$ 。这里 $x_i$ ∈{0,1}, c, $w_i$ , $p_i$ ∈ N+。

示例：
在这里插入图片描述

2. 使用自顶向下的方法

一般使用一个数组或者一个哈希map充当这个备忘录。
声明函数，并将项目、容量、临时字典和当前索引作为参数。
如果小于 0、小于 0或大于列表长度，则返回 0.
否则，如果总重量小于容量，则创建两个利润，用于检查相邻项目。这可以通过使用不同参数递归调用函数来实现。
将这两个利润中的最大值分配给字典的当前元素。将字典中的该值作为输出返回。

class Item:def __init__(self, profit, weight):self.profit = profitself.weight = weightdef zeroKnapsack(items, capacity, currentIndex, tempDict):dictKey = str(currentIndex) + str(capacity)if capacity <= 0 or currentIndex < 0 or currentIndex >= len(items):return 0elif dictKey in tempDict:return tempDict[currentIndex]elif items[currentIndex].weight <= capacity:profit1 = items[currentIndex].profit + zeroKnapsack(items, capacity-items[currentIndex].weight, currentIndex+1, tempDict)profit2 = zeroKnapsack(items, capacity, currentIndex+1, tempDict)tempDict[dictKey] = max(profit1, profit2)return tempDict[dictKey]else:return 0mango = Item(31, 3)
apple = Item(26, 1)
orange = Item(17, 2)
banana = Item(72, 5)items = [mango, apple, orange, banana]print(zeroKnapsack(items, 7, 0, {}))

3. 使用自下而上的方法

声明函数，并将利润、物品权重和背包容量作为参数。
如果容量小于 0，利润长度等于 0，或者利润长度和权重不一致，则返回 0。
创建变量：迭代行数和容量，初始化的值为 0。
创建两个变量用于存储利润。只要权重不超过容量，就存储矩阵中每一行和每一列的值。
重复上述过程，并返回两个变量的最大值作为输出。

class Item:def __init__(self, profit, weight):self.profit = profitself.weight = weightdef zoKnapsackBU(profits, weights, capacity):if capacity <= 0 or len(profits) == 0 or len(weights) != len(profits):return 0numberOfRows = len(profits) + 1dp = [[None for i in range(capacity+2)] for j in range(numberOfRows)]for i in range(numberOfRows):dp[i][0] = 0for i in range(capacity+1):dp[numberOfRows-1][i] = 0for row in range(numberOfRows-2, -1, -1):for column in range(1, capacity+1):profit1 = 0profit2 = 0if weights[row] <= column:profit1 = profits[row] + dp[row + 1][column - weights[row]]profit2 = dp[row + 1][column]dp[row][column] = max(profit1, profit2)return dp[0][capacity]profits = [31, 26, 17, 72]
weights = [3, 1, 2, 5]print(zoKnapsackBU(profits, weights, 7))