时间序列分析 - 移动平均SMA, WMA, EMA(EWMA) 之理论公式

本文主要是介绍时间序列分析 - 移动平均SMA, WMA, EMA(EWMA) 之理论公式，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原文：

https://zh.wikipedia.org/w/index.php?title=%E7%A7%BB%E5%8B%95%E5%B9%B3%E5%9D%87&variant=zh-cn#_note-0

移动平均（英语：moving average，MA），又称“移动平均线”简称均线，是技术分析中一种分析时间序列数据的工具。最常见的是利用股价、回报或交易量等变数计算出移动平均。

移动平均可抚平短期波动，反映出长期趋势或周期。数学上，移动平均可视为一种卷积。

1）SMA

简单移动平均（英语：simple moving average，SMA）是某变数之前n个数值的未作加权算术平均。例如，收市价的10日简单移动平均指之前10日收市价的平均数。若设收市价为 $p_{1}$ 至 $p_{n}$ ，则方程式为：

$SMA={p_{1}+p_{2}+\cdots +p_{n} \over n}$

当计算连续的数值，一个新的数值加入，同时一个旧数值剔出，所以无需每次都重新逐个数值加起来：

$SMA_{t1,n}=SMA_{t0,n}-{p_{1} \over n}+{p_{n+1} \over n}$

2) WMA

加权移动平均（英语：weighted moving average，WMA）指计算平均值时将个别数据乘以不同数值，在技术分析中，n日WMA的最近期一个数值乘以n、次近的乘以n-1，如此类推，一直到0：

$WMA_{M}={np_{M}+(n-1)p_{M-1}+\cdots +2p_{M-n+2}+p_{M-n+1} \over n+(n-1)+\cdots +2+1}$

由于 $WMA_{{M+1}}$ 与 $WMA_{{M}}$ 的分子相差 $np_{M+1}-p_{M}-\cdots -p_{M-n+1}$ ，假设 $p_{M}+p_{M-1}+\cdots +p_{M-n+1}$ 为总和M：

总和M+1 $=$ 总和M $+p_{M+1}-p_{M-n+1}$

分子M+1 $=N_{M+1}=$ 分子M $+np_{M+1}-$ 总和M

$WMA_{M+1}={N_{M+1} \over n+(n-1)+\cdots +2+1}$

留意分母为三角形数，方程式为 ${n(n+1) \over 2}$

下图显示出加权是随日子远离而递减，直至递减至零（N=15）。

3) EMA

指数移动平均（英语：exponential moving average，EMA或EXMA）是以指数式递减加权的移动平均。各数值的加权影响力随时间而指数式递减，越近期的数据加权影响力越重，但较旧的数据也给予一定的加权值。下图是一例子（N=15）：

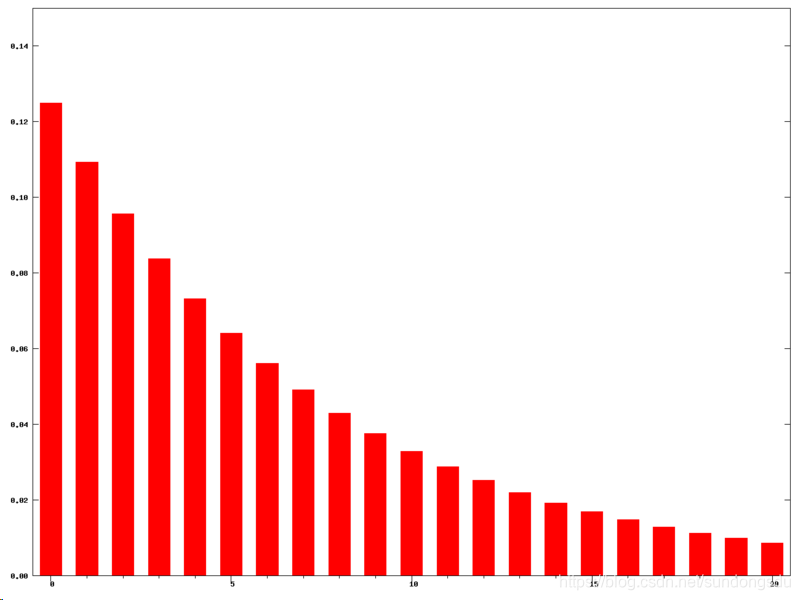
加权的程度以常数α决定，α数值介乎0至1。α也可用天数N来代表： $\alpha ={2 \over {N+1}}$ ，所以，N=19天，代表α=0.1。

设时间t的实际数值为Yt，而时间t的EMA则为St；时间t-1的EMA则为St-1，计算时间t≥2是方程式为：

$S_{t}=\alpha \times Y_{t}+(1-\alpha )\times S_{t-1}$

设今日（t1）价格为p，则今日（t1）EMA的方程式为：

${\text{EMA}}_{t1}={\text{EMA}}_{t0}+\alpha \times (p-{\text{EMA}}_{t0})$

将 ${\text{EMA}}_{t0}$ 分拆开来如下：

${\text{EMA}}={p_{1}+(1-\alpha )p_{2}+(1-\alpha )^{2}p_{3}+(1-\alpha )^{3}p_{4}+\cdots \over 1+(1-\alpha )+(1-\alpha )^{2}+(1-\alpha )^{3}+\cdots }$

理论上这是一个无穷级数，但由于1-α少于1，各项的数值会越来越细，可以被忽略。分母方面，若有足够多项，则其数值趋向1/α。即，

${\text{EMA}}=\alpha \times \left(p_{1}+(1-\alpha )p_{2}+(1-\alpha )^{2}p_{3}+(1-\alpha )^{3}p_{4}+\cdots \right)$

假设k项及以后的项被忽略，即 $\alpha \times \left((1-\alpha )^{k}+(1-\alpha )^{k+1}+\cdots \right)$ ，重写后可得 $\alpha \times (1-\alpha )^{k}\times \left(1+(1-\alpha )+(1-\alpha )^{2}\cdots \right)$ ，相当于 $(1-\alpha )^{k}$ 。所以，若要包含99.9%的加权，解方程 $k={\log(0.001) \over \log(1-\alpha )}$ 即可得出k。由于当N不断增加， $\log \,(1-\alpha )$ 将趋向 ${-2 \over N+1}$ ，简化后k大约等于 $3.45\times (N+1)$ 。