AUV直线路径跟踪仿真-反步滑模方法

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

文章目录

前言

一、整体思路

二、控制器设计

1.纵向推力-反步法

2.转艏力矩-滑模方法

三、虚拟AUV速度推算

四、仿真实现

1.艏向制导误差和滑模面函数

 2.控制器和模型解算

3.解耦速度得到艏向角和漂角

 4.积分速度得到位置信息

 5.得到位置误差和趋近角信息

6.海流干扰

7.可视化

1.位置误差

2.期望路径

3.控制力

 五、仿真结果分析

前言

本文进行AUV水平面的直线路径跟踪的控制设计和simulink的仿真搭建。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、整体思路

将整个AUV系统进行解耦，将直线路径跟踪问题转化为对AUV速度和艏向角的控制，并分别设计控制器，其中，纵向速度控制时运用反步法进行控制器设计，艏向角控制则利用滑模方法。在本文中，所涉及的AUV含有主推和垂直舵，属于欠驱动，缺少横向输入。

二、控制器设计

1.纵向推力-反步法

期望速度，根据反步法原理进行设计，具体参考：

AUV控制中的反步法_工程湛湛的博客-CSDN博客

得到的控制力应当为：

为进一步增强控制性能，结合李雅普诺夫函数的一阶导小于零的要求，在控制率中引入了有利于控制的非线性项：

则纵向推力重新变为：

2.转艏力矩-滑模方法

在进行转艏力矩的设计之前，需要先了解两个知识点，一个是Serret-Frenet坐标系，另一个是视线法。参考：

基于Serret-Frenet坐标系下的跟踪误差方程_工程湛湛的博客-CSDN博客

AUV路径跟踪视线法（Line Of Sight）制导原理_工程湛湛的博客-CSDN博客

根据AUV视线法的制导原理，需要AUV的航迹角与SF坐标系与定系夹角的差值向趋近角趋近，此时我们定义趋近误差为：

通过滑模方法进行转艏力矩控制器设计的过程参考：

滑模方法设计AUV路径跟踪转艏力矩_工程湛湛的博客-CSDN博客

最后得到的控制率为：

至此，便得到了纵向推力和转艏力矩的控制率。

三、虚拟AUV速度推算

参考：虚拟向导AUV的速度推算_工程湛湛的博客-CSDN博客

得到的三维虚拟向导速度为：

结合水平面的特点,，则：

根据输入，在Simulink中得到s的一阶导：

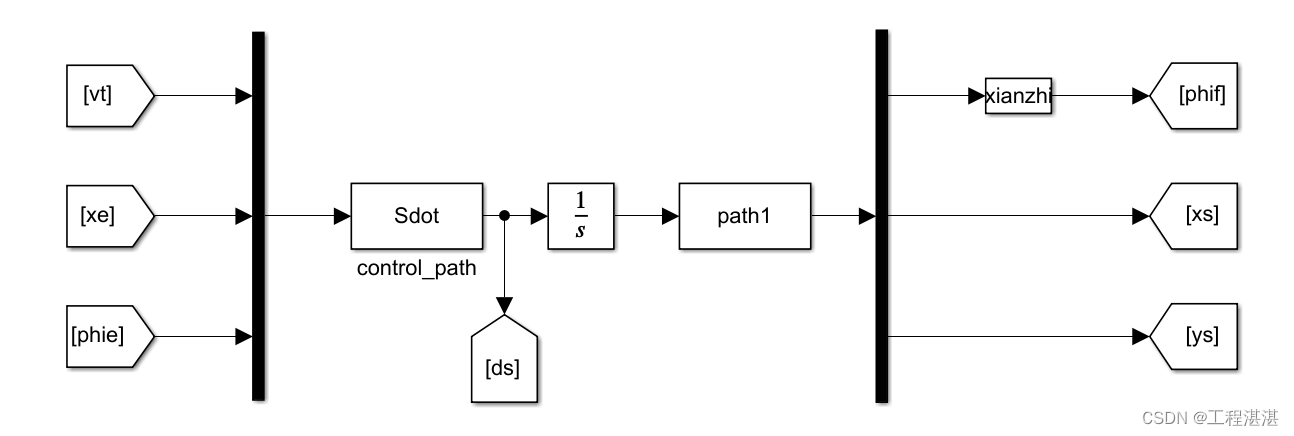
上式中phie为定系与SF坐标系的夹角：

 随后在path1的s函数中定义所要跟踪的期望路径，输出期望路径的SF坐标系与定系的夹角和横向期望路径和纵向期望路径信息。

四、仿真实现

以下按照笔者思路，进行整个Simulink仿真程序的复现。

1.艏向制导误差和滑模面函数

首先得到AUV的航迹角和SF坐标系与定系的夹角：

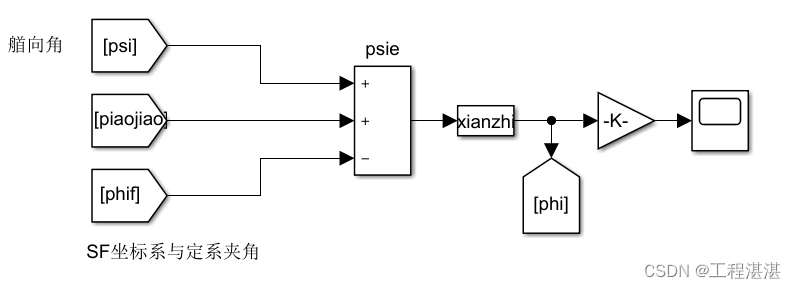
得到phi角，通过该角对趋近角的趋近即可完成AUV的制导，因此得到的误差角为：

 根据误差得到的滑模面函数为：

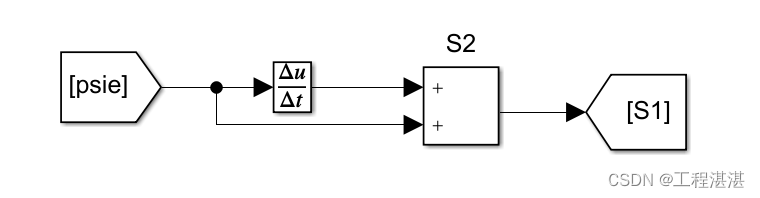
 2.控制器和模型解算

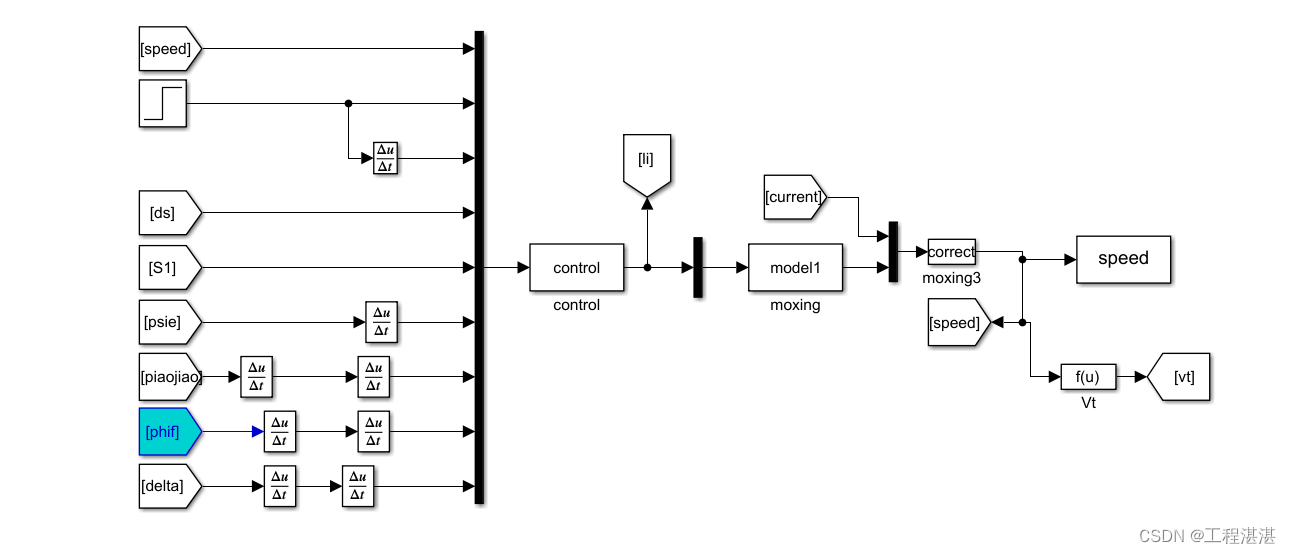
 根据所设计的纵向推力和转艏力矩，设计一系列的输入，得到控制力的输出：

得到控制力后输入到AUV的水平面动力学模型进行解算，从而得到AUV的速度信息，水平面的模型表示为：

 仿真中current为海流干扰，通过相对速度对AUV的速度进行修正，即correct，最后输出AUV的纵向速度、横向速度和转艏角速度，并计算出AUV的和速度vt。

3.解耦速度得到艏向角和漂角

对模型解算得到的速度信息解耦，计算得到艏向角信息：

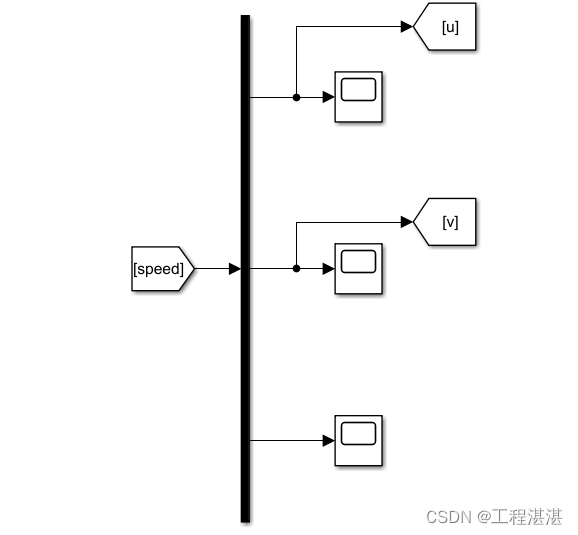
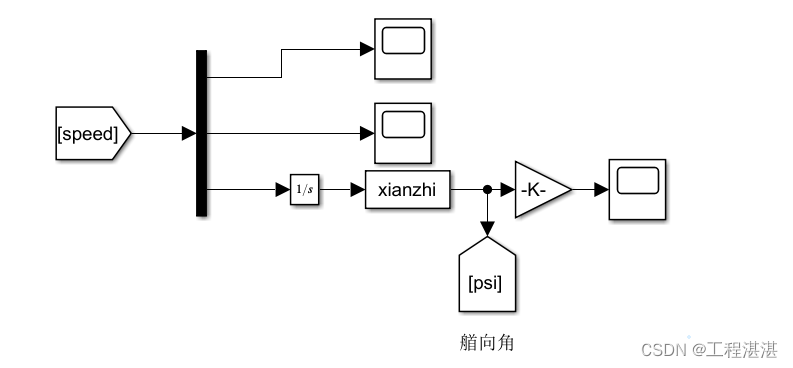
由横向速度和纵向速度得到漂角信息：

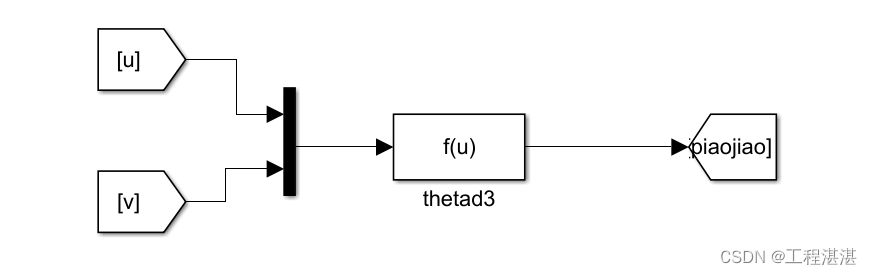
 4.积分速度得到位置信息

对得到的速度信息进行积分处理，同时设置位置的初始值，便可得到AUV的实时位置信息：

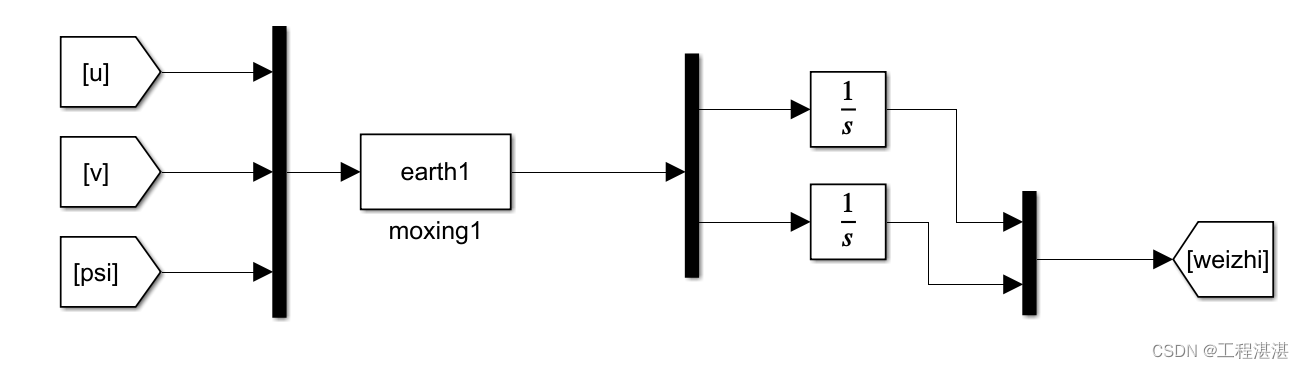
 在积分器中进行初始值的设置。

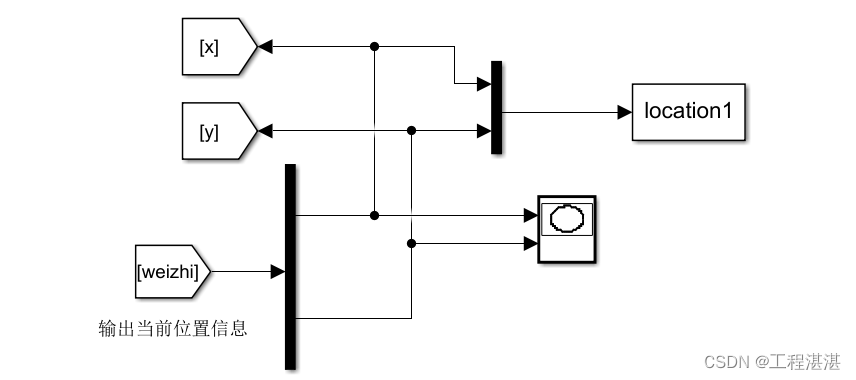
 5.得到位置误差和趋近角信息

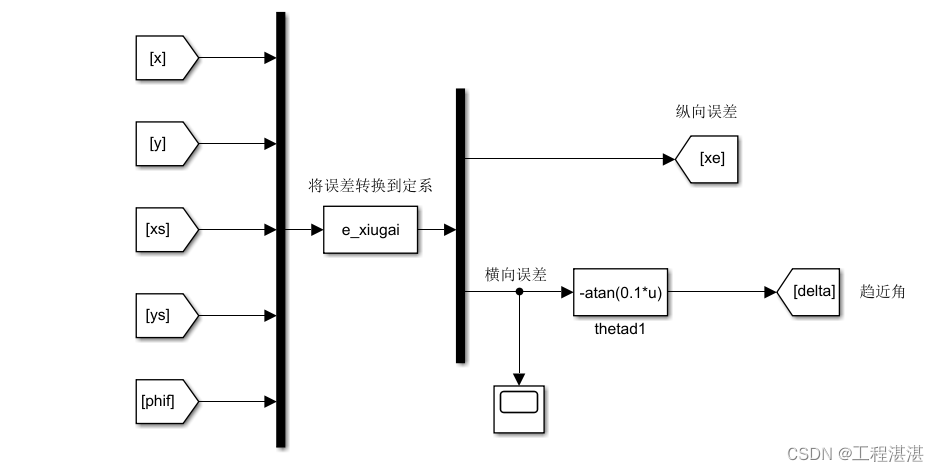
通过得到对速度积分得到的实时位置信息，以及SF坐标系得到的期望路径信息，做差得到误差信息，再通过坐标变换将误差转换到定系，转换角为phif，在得到横向误差之后计算得到趋近角。

6.海流干扰

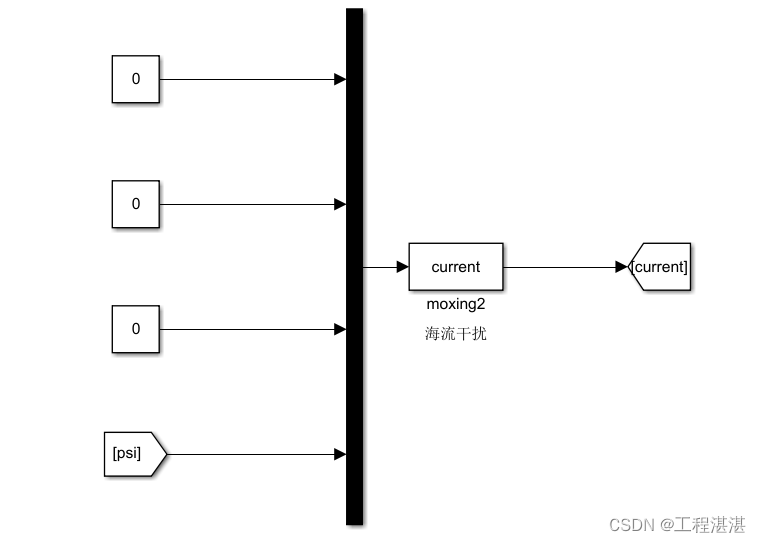
通过设置AUV在定系中的速度，然后通过艏向角将速度转换到动系，便得到了在动系下的海流速度信息，和AUV速度进行做差，便得到了AUV相对海流的相对速度。

7.可视化

1.位置误差

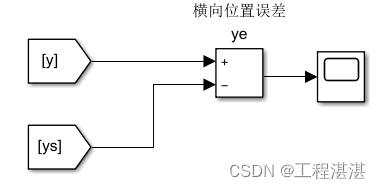
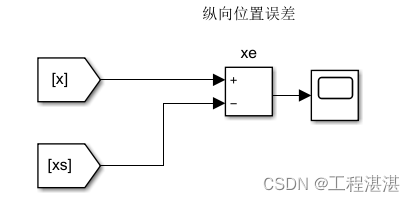
2.期望路径

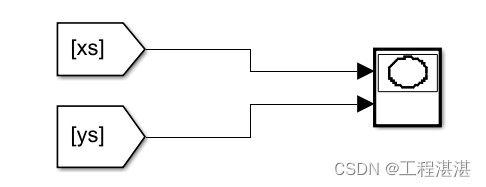
3.控制力

---

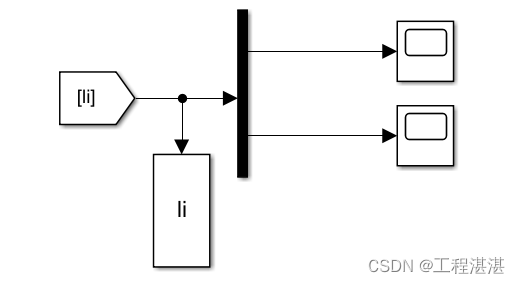
 五、仿真结果分析

搭建完后设置仿真时间为200s运行，得到的仿真结果。

纵向速度：

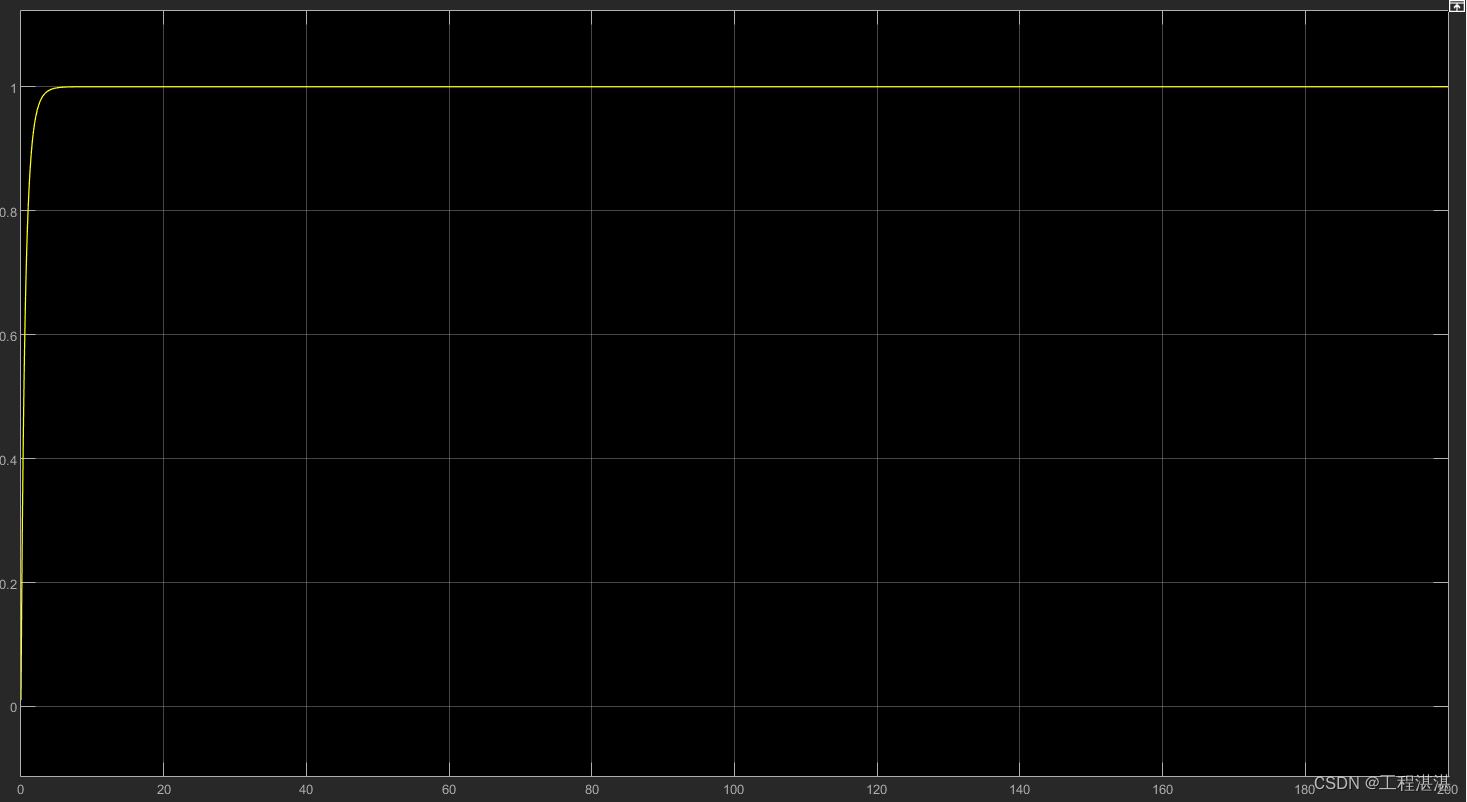
横向速度：

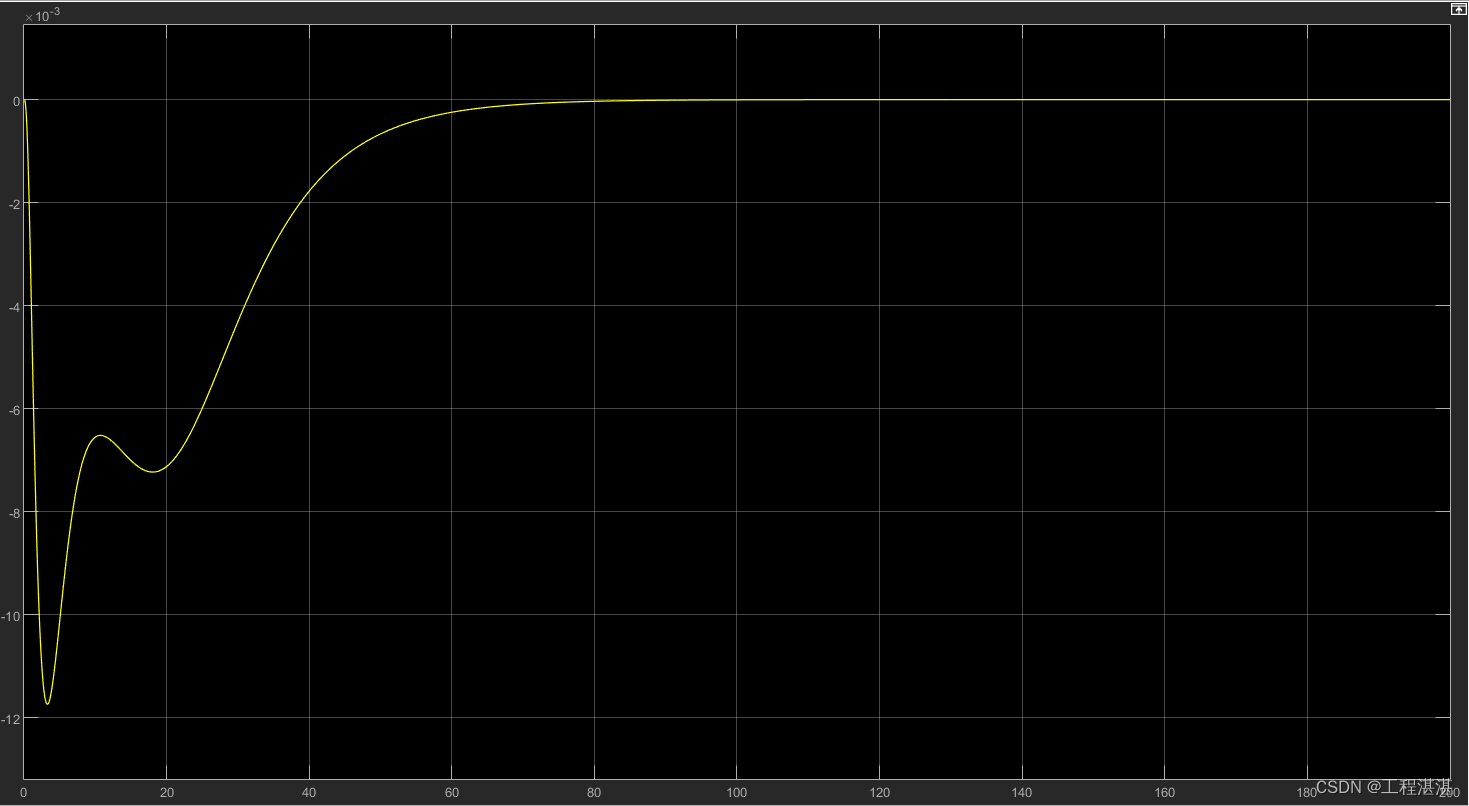
艏向角速度：

 纵向推力：

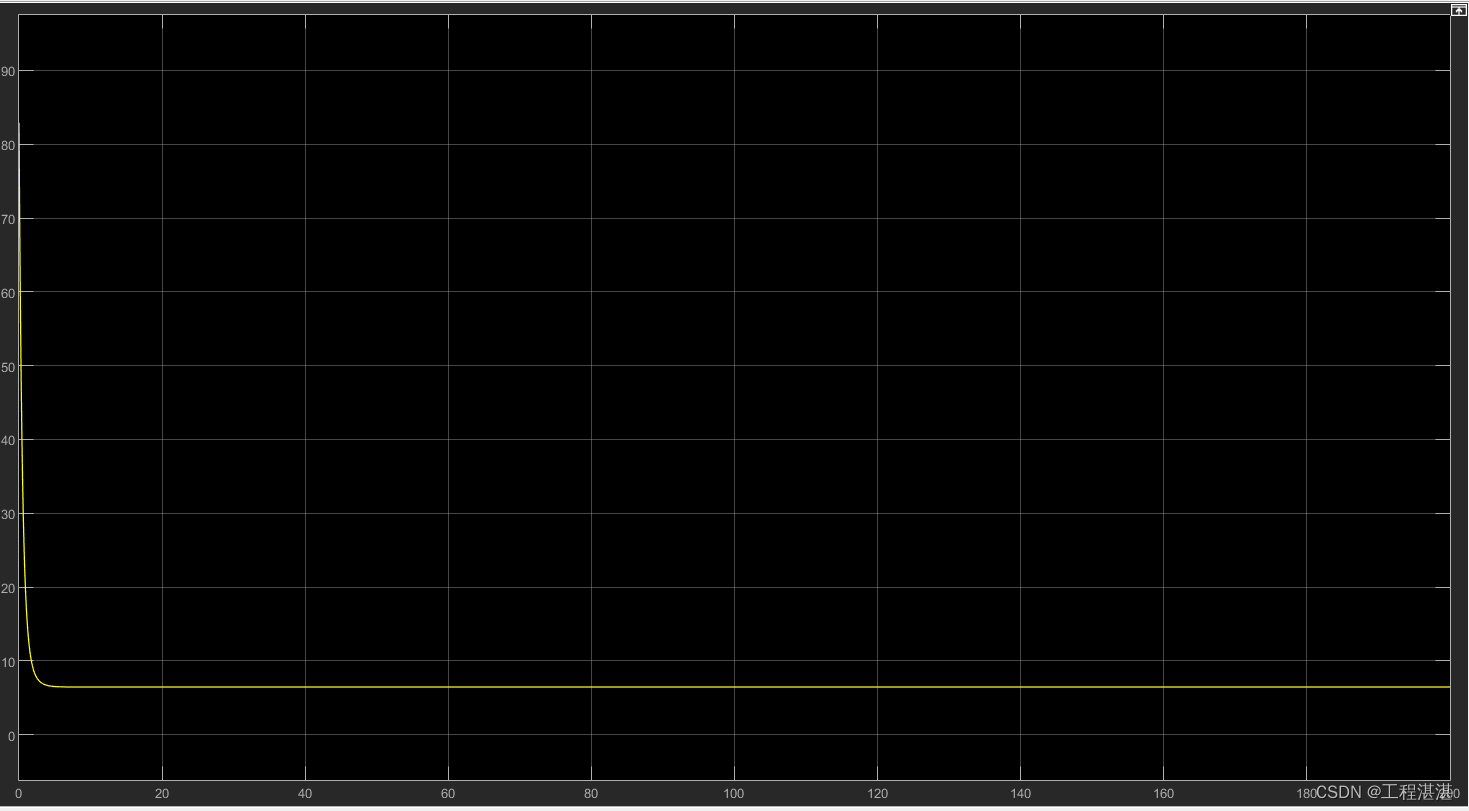
转艏力矩：

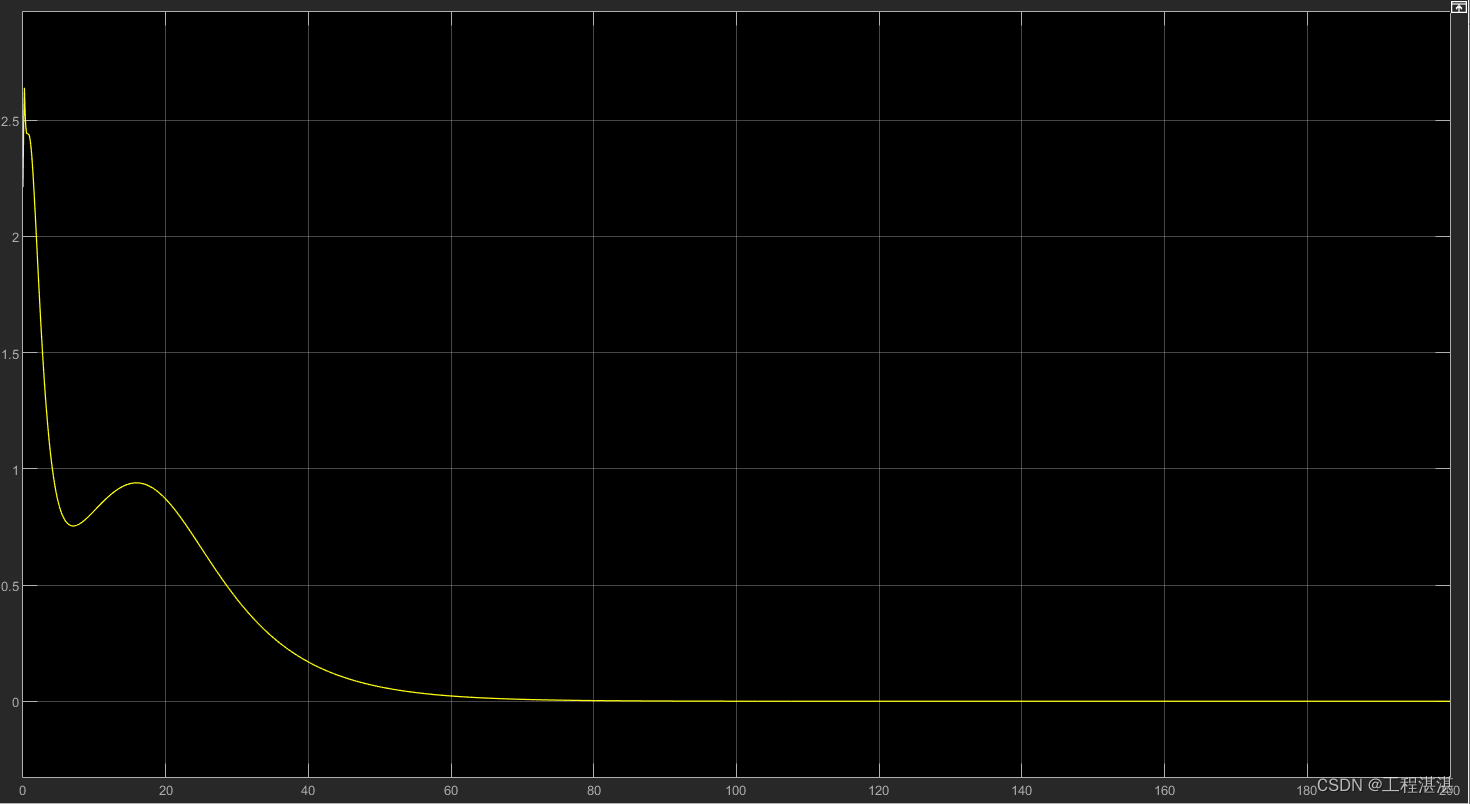
 横向位置误差：

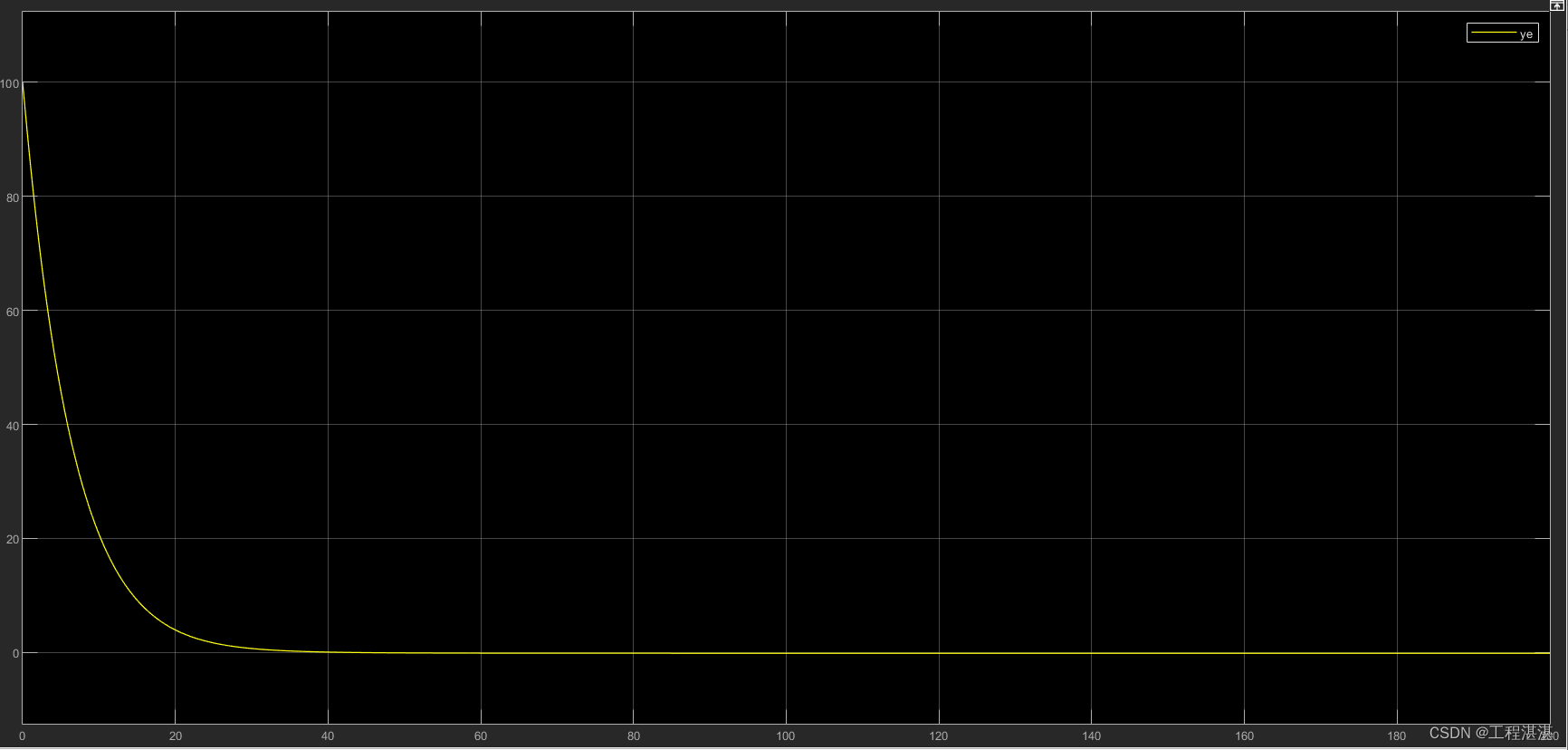
 纵向位置误差：

 制导误差角信息：

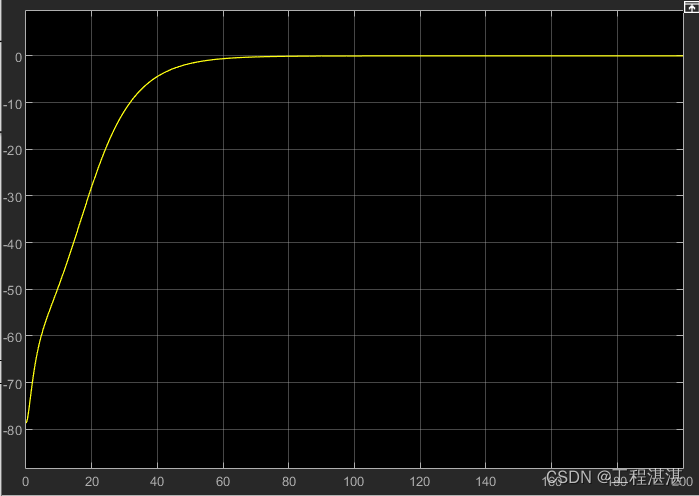
 期望路径二维图：

AUV位置二维图像：

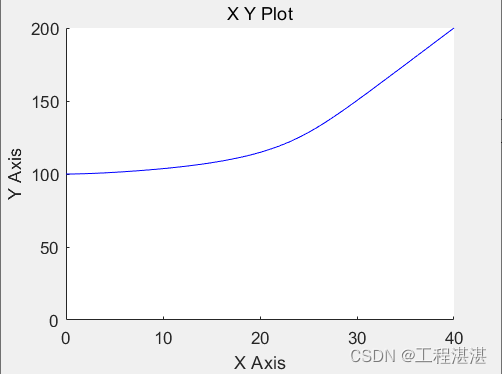
 从仿真结果来看，AUV的跟踪效果良好，说明了所设计控制器的有效性。