本文主要是介绍排序决战(2)堆排序——详细之详细,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在上期讲完了希尔排序和插入排序后,我们的希尔排序成功胜出,这一期,我们继续,这次决战的是堆排序小姐

堆排序
概念:
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
1.先把入的数据建堆成大堆(升序)/小堆(降序)
2.建成大堆/小堆后再进行取堆顶和堆底交换,进行依次向下调整,所以我们会用到向上调整和向下调整算法,即可完成堆排序
如图所示:
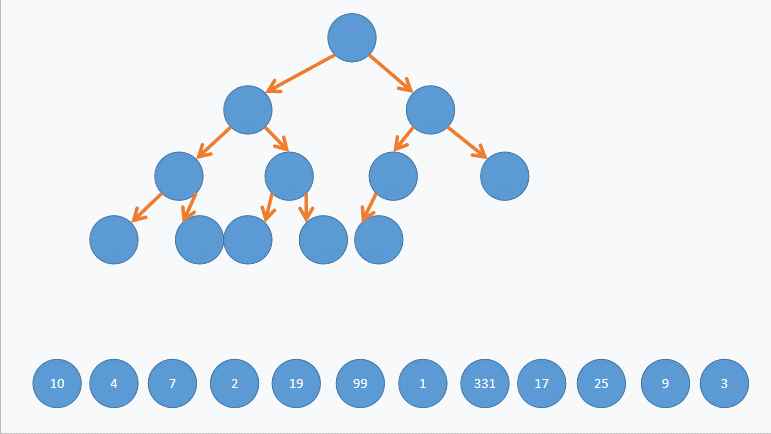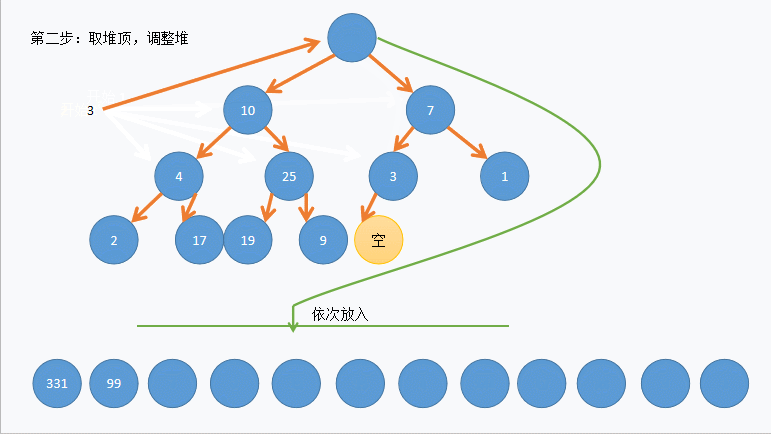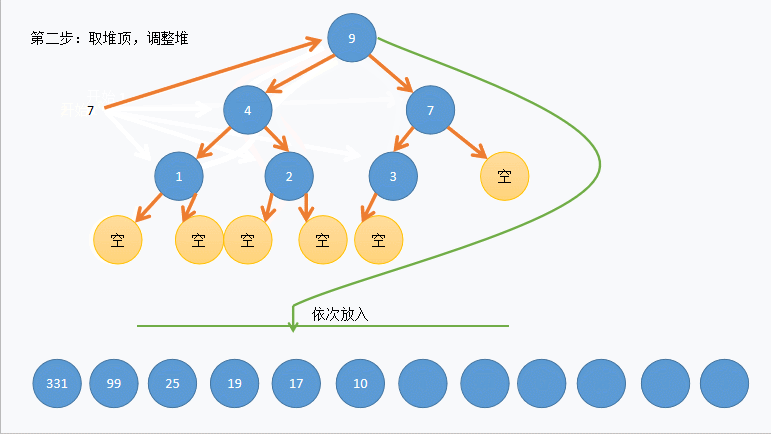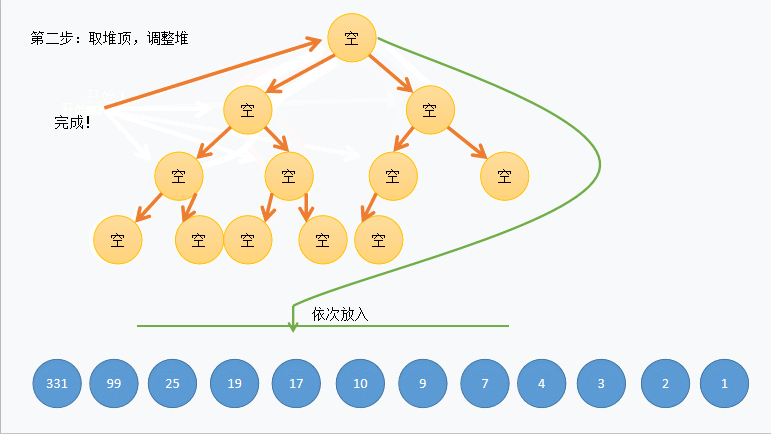
首先我们来讲解向上调整和向下调整算法:
向上调整算法:
有如下的堆:9,8,6,5,6,1
当我们想要插入堆数的时候,并且让堆保持堆的性质,我们应该如何操作
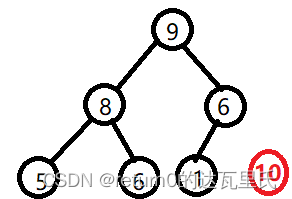
当我们把他调整为一个大堆/小堆,那么我们就会拿父亲节点和子节点比较,如果父亲节点大于/小于子节点的时候,则交换子节点,一直交换到父亲节点大于子节点的时候,便不进行交换了。
如图所示:
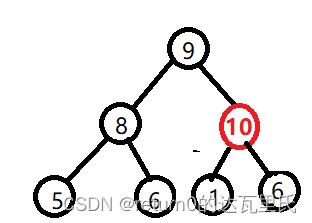
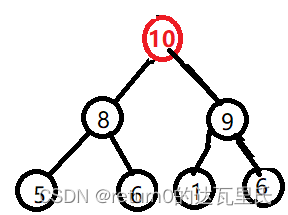
代码如下:
//向上调整 大堆
void AdjustUp(int* a,int child) {int parent = (child - 1) / 2;while (child>0){if (a[parent]<a[child]){Swap(&a[parent], &a[child]);child=parent;parent = (child - 1) / 2;} else{break;}}
}值得一提的是,我们堆的物理结构是数组,在数组中,我们应该如何得到他的父亲节点呢?
如图:红色的是下标

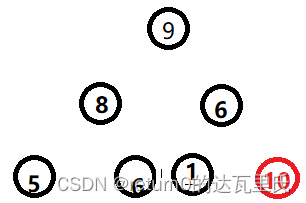
看图可知我们则只需要让下标-1/2就好了
向下调整算法:
向下调整算法是整个堆排序的核心,
!但是最主要的一个==前提==就是根节点的左右子树都要是大堆或者都要是小堆,就根结点不满足,才可以去进行一个向下调整!
与向上调整算法类似,找子节点进行比较交换,一直到向下的子节点都符合堆的特性,不过在代码这里,我们有很多点要小心
void AdjustDown(int* a, int size, int parent) {//建大堆int child = parent*2+1;while (child<size){if (child+1<size&&a[child] < a[child + 1]){child++;//假设法}if (a[child]>a[parent]){Swap(&a[child],&a[parent]);parent = child;child = parent * 2 + 1;}else{break; }}
}
在这里我们往下调整的时候,需要和左节点与右节点的最大一个换,那么,问题来了,我们怎么才能知道哪个是最大的呢?
这里,我们可以使用假设法,我们假设左节点/右节点最大,然后进行左节点和右节点的比较
知道父亲节点下标,求孩子节点下标
father = 0 :
左孩子 = father * 2 + 1 = 1;
右孩子 = father * 2 + 2 = 2;
father = 2:
左孩子 = father * 2 + 1 = 5;
右孩子 = father * 2 + 2 = 6;
如果右节点比左节点大,那么便更新成为右节点为最大的节点,向下调整。如图: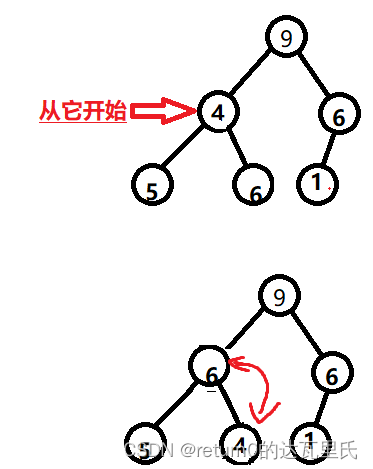
排序
开头讲了排序会用到以上两种算法,首先是建堆,然后进行与第n个交换向下调整,然后再和n--进行交换,循环进行。
误区:
在这里,排升序的时候,如果按我们正常很流畅的逻辑来讲,我们自然的会去建小堆,但是事实真是如此吗?我们可以画个图来看看
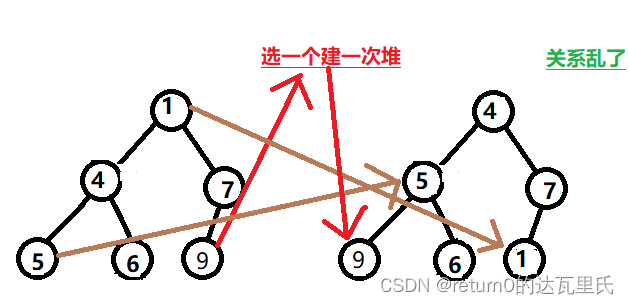
由此可见,当要排升序的时候建小堆不是个明智的决定,而你觉得的,也不一定就是你觉得的,实践出真知,建小堆不仅关系会乱,而且效率也不高,所以,我们选择建大堆试试
如图所示:
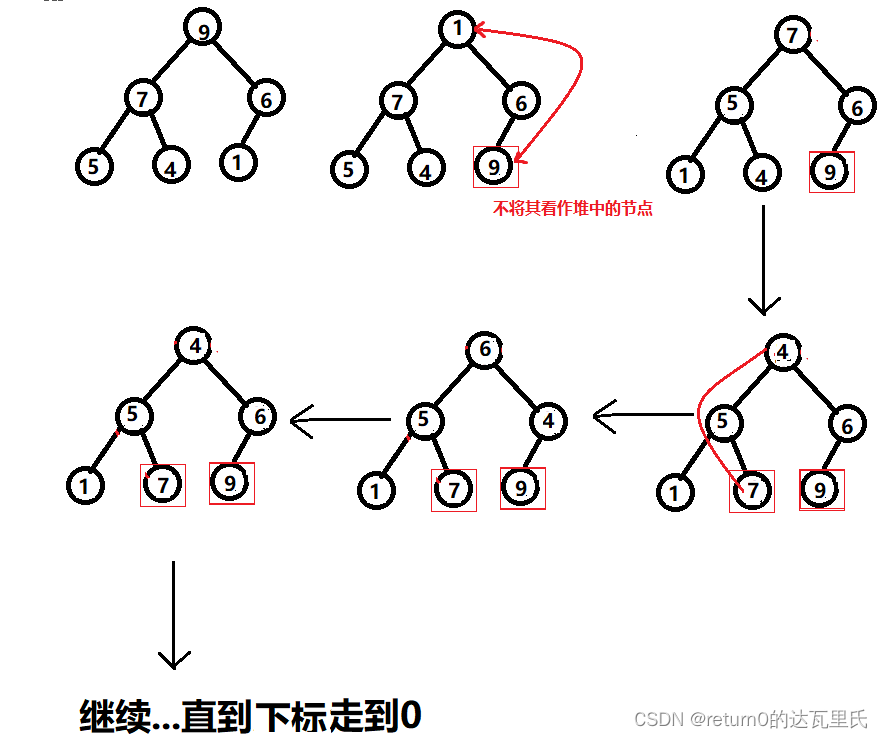
如上图,红方框的已经按升序排好了,接下来一直排序到下标0就好了。
对照代码,来欣赏一下我们的堆排序小姐罢!
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//向上调整 大堆
void AdjustUp(int* a,int child) {int parent = (child - 1) / 2;while (child>0){if (a[parent]<a[child]){Swap(&a[parent], &a[child]);child=parent;parent = (child - 1) / 2;} else{break;}}
}
void AdjustDown(int* a, int size, int parent) {//建大堆int child = parent*2+1;while (child<size){if (child+1<size&&a[child] < a[child + 1]){child++;//假设法}if (a[child]>a[parent]){Swap(&a[child],&a[parent]);parent = child;child = parent * 2 + 1;}else{break; }}
}
void HeapSort(int* a, int size) {//建堆for (int i = 1; i < size; i++){AdjustUp(a, i);}int end = size - 1;for (int i = end; i >0; i--)//排序{Swap(&a[end], &a[0]);AdjustDown(a, end, 0);end--;}
}
时间复杂度分析
堆排序分作两个部分,
一是建堆,建堆要一个一个建,自然时间复杂度是On
二才是排序,调整这一块的话就是每次够把当前堆中最的数放到堆底来,然后每一个次大的数都需要向下调整O(log2N),数组中有N个数需要调整做排序,因而就是O(Nlog2N)
最后将两段代码整合一下,就是O(N + Nlog2N),取影响结果大的那一个就是O(Nlog2N),这也就是堆排序最终的时间复杂度
测试:
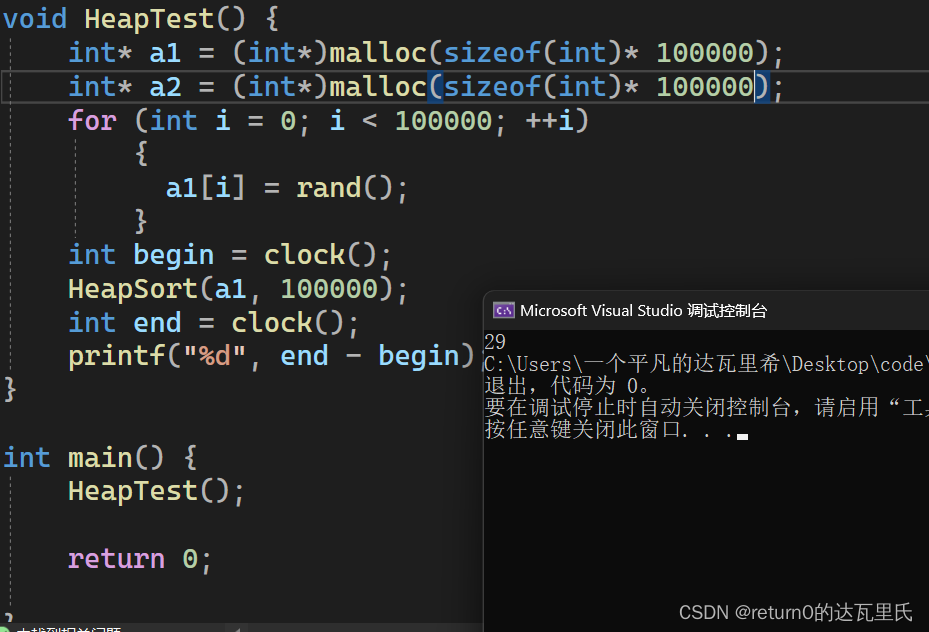
可见,堆排序小姐速度并不算慢,比插入排序可快多了,但是已经略逊于我们上期的冠军,希尔 排序了
所以这一集,仍然是希尔排序胜利!
这篇关于排序决战(2)堆排序——详细之详细的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





