本文主要是介绍含电热联合系统的微电网运行优化附Matlab代码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
智能优化算法 神经网络预测 雷达通信 无线传感器
信号处理 图像处理 路径规划 元胞自动机 无人机 电力系统
⛄ 内容介绍
在当前能源互联网迅速发展及电热联系日渐紧密的环境下,提出基于电热联合调度的区域并网型微电网运行优化模型.综合网内储能特性,分时电价,电热负荷与分布式电源的时序特征,以包含风机,光伏电池,热电联产系统,电锅炉,燃料电池和储能系统的并网型微电网为例,采用Cplex优化软件求得调度周期内各微电源最佳出力及总运行成本,并与两种常见电热调度方式进行比较.仿真算例表明:联合调度模型能实现电热统一协调调度并降低微电网运行成本.该模型可为电热之间能源互联及规划运营提供参考.
⛄ 部分代码
function f = initialize_variables(N, M, V, min_range, max_range, time, Zall, ComC0)
min = min_range;
max = max_range;
% K is the total number of array elements. For ease of computation decision
% variables and objective functions are concatenated to form a single
% array. For crossover and mutation only the decision variables are used
% while for selection, only the objective variable are utilized.
number_of_decision_variables.c = V(1,1);
number_of_decision_variables.t = V(2,1);
K = M + 2 * V(1,1) + 2 * V(2,1);
StepComC = 1; %变量的离散化
StepT1 = 0.025;
StepT2 = 0.025;
%% Initialize each chromosome
% For each chromosome perform the following (N is the population size)
for i = 1 : N
for j= 1 : number_of_decision_variables.c
f(i,j) = min.c(j,1) + (max.c(j,1) - min.c(j,1))*rand(1);
f(i,j + number_of_decision_variables.c) = min.c(j,2) + (max.c(j,2) - min.c(j,2))*rand(1);
%f(i,j)离散化
ComCC(j)= f(i,j);
ComCC1(j) = abs(ComCC(j)) / StepComC;
%Tap1 = Tap ./ StepTap;
ComCC2(j) = fix(ComCC1(j)); %商
ComCC3(j) = abs(ComCC(j)) - ComCC2(j) * StepComC;%余
ComCC2(j) = ComCC2(j) * StepComC;
%Tap = Tap1 - fix(Tap1);
if ComCC3(j) > (StepComC / 2)
ComCC3(j) = StepComC - ComCC3(j);
ComCC2(j) = ComCC2(j) + StepComC;
end
if f(i,j)>0
f(i,j) = ComCC2(j);
else
f(i,j) = - ComCC2(j);
end
%检验f(i,j)中无重复
pf(1,:) = f(i,1:number_of_decision_variables.c);
for w = 1 : number_of_decision_variables.c
for ww = (w + 1) : number_of_decision_variables.c
while f(i,w) == pf(1,ww)
f(i,w) = min.c(j,1) + (max.c(j,1) - min.c(j,1))*rand(1);
ComCC(j)= f(i,w);
ComCC1(j) = abs(ComCC(j)) / StepComC;
%Tap1 = Tap ./ StepTap;
ComCC2(j) = fix(ComCC1(j)); %商
ComCC3(j) = abs(ComCC(j)) - ComCC2(j) * StepComC;%余
ComCC2(j) = ComCC2(j) * StepComC;
%Tap = Tap1 - fix(Tap1);
if ComCC3(j) > (StepComC / 2)
ComCC3(j) = StepComC - ComCC3(j);
ComCC2(j) = ComCC2(j) + StepComC;
end
if f(i,w)>0
f(i,w) = ComCC2(j);
else
f(i,w) = - ComCC2(j);
end
end
end
end
%f(i,j + number_of_decision_variables)离散化
ComCC(j)= f(i,j + number_of_decision_variables.c);
ComCC1(j) = abs(ComCC(j)) / StepComC;
%Tap1 = Tap ./ StepTap;
ComCC2(j) = fix(ComCC1(j)); %商
ComCC3(j) = abs(ComCC(j)) - ComCC2(j) * StepComC;%余
ComCC2(j) = ComCC2(j) * StepComC;
%Tap = Tap1 - fix(Tap1);
if ComCC3(j) > (StepComC / 2)
ComCC3(j) = StepComC - ComCC3(j);
ComCC2(j) = ComCC2(j) + StepComC;
end
if f(i,j + number_of_decision_variables.c)>0
f(i,j + number_of_decision_variables.c) = ComCC2(j);
else
f(i,j + number_of_decision_variables.c) = - ComCC2(j);
end
end
for j= 1 : number_of_decision_variables.t
f(i,j + 2 * V(1,1)) = min.t(j,1) + (max.t(j,1) - min.t(j,1))*rand(1);
f(i,j + 2 * V(1,1) + number_of_decision_variables.t) = min.t(j,2) + (max.t(j,2) - min.t(j,2))*rand(1);
%f(i,j)离散化
ComCC(j)= f(i,j + 2 * V(1,1));
ComCC1(j) = abs(ComCC(j)) / StepT1;
%Tap1 = Tap ./ StepTap;
ComCC2(j) = fix(ComCC1(j)); %商
ComCC3(j) = abs(ComCC(j)) - ComCC2(j) * StepT1;%余
ComCC2(j) = ComCC2(j) * StepT1;
%Tap = Tap1 - fix(Tap1);
if ComCC3(j) > (StepT1 / 2)
ComCC3(j) = StepT1 - ComCC3(j);
ComCC2(j) = ComCC2(j) + StepT1;
end
if f(i,j)>0
f(i,j + 2 * V(1,1)) = ComCC2(j);
else
f(i,j + 2 * V(1,1)) = - ComCC2(j);
end
%f(i,j + 2 * V(1,1) + number_of_decision_variables)离散化
ComCC(j)= f(i,j + 2 * V(1,1) + number_of_decision_variables.t);
ComCC1(j) = abs(ComCC(j)) / StepT2;
%Tap1 = Tap ./ StepTap;
ComCC2(j) = fix(ComCC1(j)); %商
ComCC3(j) = abs(ComCC(j)) - ComCC2(j) * StepT2;%余
ComCC2(j) = ComCC2(j) * StepT2;
%Tap = Tap1 - fix(Tap1);
if ComCC3(j) > (StepT2 / 2)
ComCC3(j) = StepT2 - ComCC3(j);
ComCC2(j) = ComCC2(j) + StepT2;
end
if f(i,j + 2 * V(1,1) + number_of_decision_variables.t)>0
f(i,j + 2 * V(1,1) + number_of_decision_variables.t) = ComCC2(j);
else
f(i,j + 2 * V(1,1) + number_of_decision_variables.t) = - ComCC2(j);
end
end
f(i, 2 * V(1,1) + 2 * V(2,1) + 1 : K) = evaluate_objective(f(i,:),M ,V ,time, Zall, ComC0);
end
⛄ 运行结果
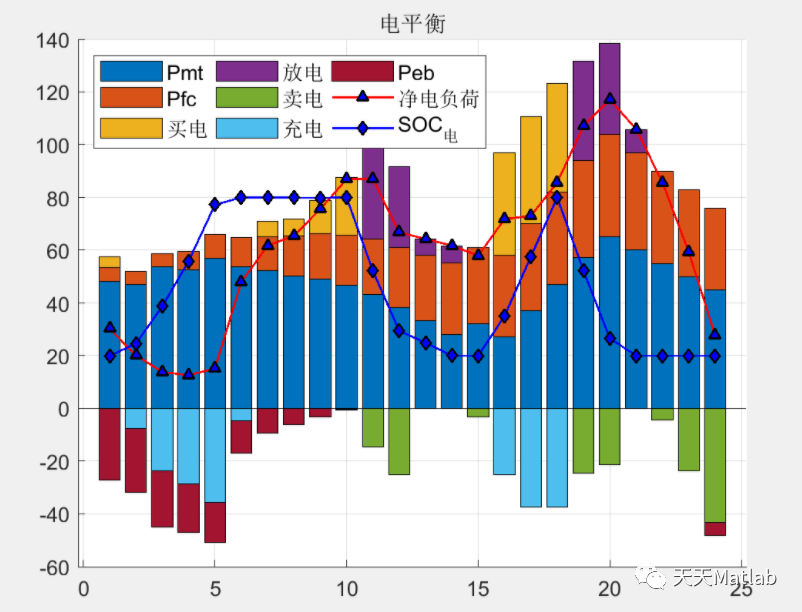
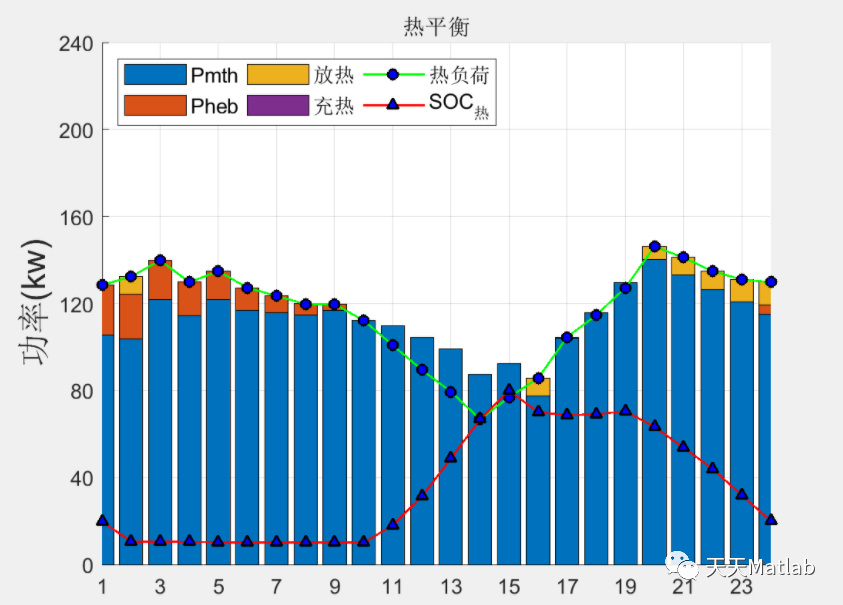
⛄ 参考文献
[1]李正茂, 张峰, 梁军,等. 含电热联合系统的微电网运行优化[J]. 中国电机工程学报, 2015, 35(14):3569-3576.
⛄ Matlab代码关注
❤️部分理论引用网络文献,若有侵权联系博主删除
❤️ 关注我领取海量matlab电子书和数学建模资料
这篇关于含电热联合系统的微电网运行优化附Matlab代码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





