leetcode刷题542. 01 矩阵（Java）DFS+BFS+DP

本文主要是介绍leetcode刷题542. 01 矩阵（Java）DFS+BFS+DP，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.题目描述

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例1：

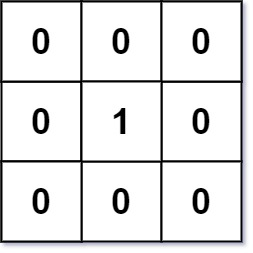
输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

示例2：

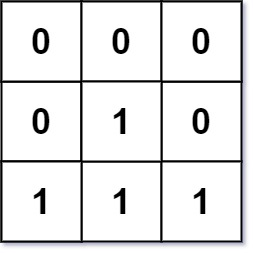
输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

提示：

m == mat.length
n == mat[i].length
1 <= m, n <= 104
1 <= m * n <= 104
mat[i][j] is either 0 or 1.
mat 中至少有一个 0

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/01-matrix
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2.解法

2.1 深度优先搜索（DFS）递归实现

因为0和靠近0的1是不需要改变的。
所以首先将矩阵初始化，将需要计算距离的点全初始化为最大值。
之后通过递归，从1开始向离0远的地方寻找还未计算过距离的点同时更新最短距离。

class Solution {int dx[] = {1,0,0,-1};//左右移动int dy[] = {0,1,-1,0};//上下移动int m,n;public int[][] updateMatrix(int[][] mat) {m = mat.length;if(m==0){return mat;}n = mat[0].length;for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(mat[i][j]==1&&isNeiborZero(mat,i,j)==false){mat[i][j]=Integer.MAX_VALUE;//将矩阵初始化，以便之后遍历}}}for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(mat[i][j]==1){dfs(mat,i,j);//从1向内部递归}}}return mat;}boolean isNeiborZero(int [][]mat,int x,int y){//判断周围是否有0for(int i=0;i<4;i++){for(int j=0;j<4;j++){int mx = x+dx[i];int my = y+dy[i];if(mx>=0&&mx<m&&my>=0&&my<n&&mat[mx][my]==0){return true;}}}return false;}void dfs(int [][]mat,int x,int y){for(int i=0;i<4;i++){for(int j=0;j<4;j++){int mx = x+dx[i];int my = y+dy[i];if(mx>=0&&mx<m&&my>=0&&my<n&&mat[mx][my]>mat[x][y]+1){mat[mx][my] = mat[x][y] +1;dfs(mat,mx,my);}}}}
}

2.2 广度优先搜索（BFS）

广度优先搜索需要用到队列Java队列，可以从这里复习。

广度优先搜索官方题解讲的很好。

我的理解就是通过队列管理计算过距离的点，计算过的点就放入队列，通过while循环队列从0向外开始计算，先从队列中取出一个点计算上下左右如果有计算过的点就放入队列，并记录一下已经访问过的点，防止进入死循环。

当队列为空时说明了所有的点都已经计算过了。

代码如下

class Solution {int dx[]={1,0,0,-1};//左右移动int dy[]={0,1,-1,0};//上下移动int m,n;public int[][] updateMatrix(int[][] mat) {m = mat.length;if(m==0){return mat;}n = mat[0].length;int[][] newMat = new int[m][n];//存储计算过的距离boolean[][] seen = new boolean[m][n];//存储是否访问过该点Queue<int[]> queue = new LinkedList<int[]>();//用二维队列存储需要访问四周的额点for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(mat[i][j]==0){queue.offer(new int[]{i,j});//将0点存入队列seen[i][j]=true;newMat[i][j]=0;}}}while(!queue.isEmpty()){int []cell = queue.poll();int x = cell[0],y = cell[1];for(int i=0;i<4;i++){int mx = x+dx[i],my=y+dy[i];if(mx>=0&&mx<m&&my>=0&&my<n&&!seen[mx][my]){newMat[mx][my] = newMat[x][y]+1;//计算距离queue.offer(new int[]{mx,my});seen[mx][my] = true; }}}return newMat;}
}

2.3 动态规划（DP）

动态规划最重要的就是状态转移方程。
我的理解就是从终点向前走一步离起点更近，而终点可以用一个值+更近的点表示。

以下是我的理解，相当于官方题解的缩略版。

从1到0，一共有上下左右四个方向。
而上下和左右结合，共有四种方法。

• 只有 水平向左移动 和 竖直向上移动；
• 只有 水平向左移动 和 竖直向下移动；
• 只有 水平向右移动 和 竖直向上移动；
• 只有 水平向右移动 和 竖直向下移动。

假如1在0的右下方，则1需要向左移动和向上移动，此时的状态转移方程就是。

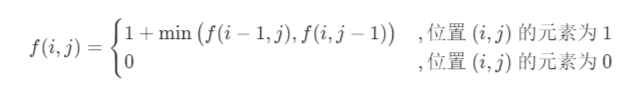
可以类推出来剩下的方程。
代码如下：

class Solution {public int[][] updateMatrix(int[][] mat) {int m = mat.length;if(m==0){return mat;}int n = mat[0].length;int [][]newMat = new int[m][n];for(int i=0;i<m;i++){Arrays.fill(newMat[i],Integer.MAX_VALUE/2);}//首先填入0for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(mat[i][j]==0){newMat[i][j]=0;}}}//向右向上for(int i=0;i<m;i++){for(int j=n-1;j>=0;j--){if(i-1>=0){newMat[i][j]=Math.min(newMat[i-1][j]+1,newMat[i][j]);}if(j+1<n){newMat[i][j]=Math.min(newMat[i][j+1]+1,newMat[i][j]);}}}//向左向上for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(i-1>=0){newMat[i][j]=Math.min(newMat[i-1][j]+1,newMat[i][j]);}if(j-1>=0){newMat[i][j]=Math.min(newMat[i][j-1]+1,newMat[i][j]);}}}//向左向下for(int i=m-1;i>=0;i--){for(int j=0;j<n;j++){if(i+1<m){newMat[i][j]=Math.min(newMat[i+1][j]+1,newMat[i][j]);}if(j-1>=0){newMat[i][j]=Math.min(newMat[i][j-1]+1,newMat[i][j]);}}}//向右向下for(int i=m-1;i>=0;i--){for(int j=n-1;j>=0;j--){if(i+1<m){newMat[i][j]=Math.min(newMat[i+1][j]+1,newMat[i][j]);}if(j+1<n){newMat[i][j]=Math.min(newMat[i][j+1]+1,newMat[i][j]);}}}return newMat;}
}

这篇关于leetcode刷题542. 01 矩阵（Java）DFS+BFS+DP的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---