本文主要是介绍9.7不同的二叉搜索树(LC96-M),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

96. 不同的二叉搜索树 - 力扣(LeetCode)
算法:
看到这道题的时候有点懵,可以举几个例子,找规律

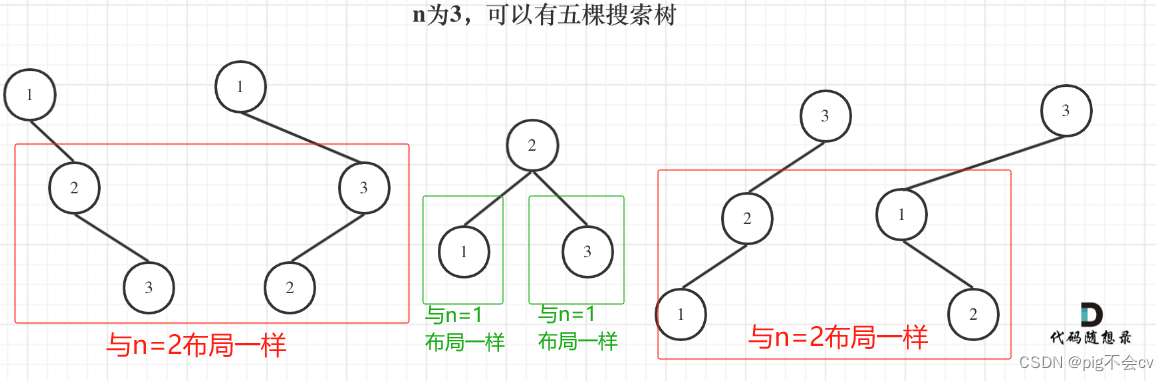
n为3的时候:
当1为头结点的时候,其右子树有两个节点,两个节点的布局, 和n 为2的时候两棵树的布局一样
(可能有同学问了,这布局不一样啊,节点数值都不一样。别忘了我们就是求不同树的数量,并不用把搜索树都列出来,所以不用关心其具体数值的差异)
当3为头结点的时候,其左子树有两个节点,两个节点的布局, 和n 为2的时候两棵树的布局一样
当2为头结点的时候,其左右子树都只有一个节点,两个节点的布局, 和n 为1的时候两棵树的布局一样
到这里,我们发现可以通过dp[1] 和 dp[2] 来推导出来dp[3]的某种方式。
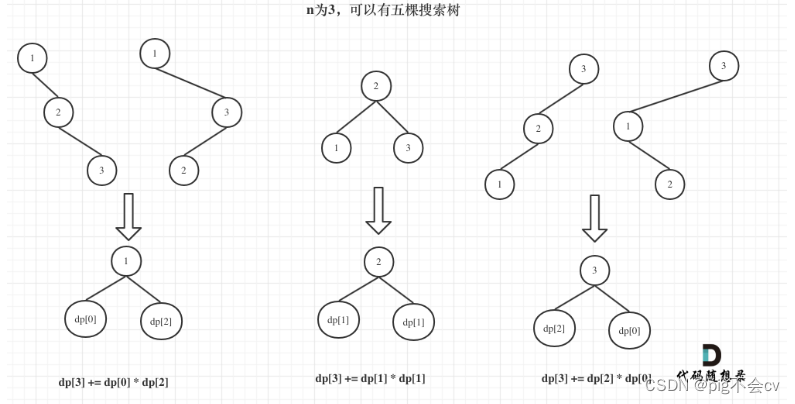
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
动规五部曲:
1.确定dp数组及下标
dp[i]:i个不同元素节点组成的二叉搜索树的个数为dp[i]
2.确定递推公式
dp[i] += dp[以j为头结点左子树节点数量] * dp[以i-1-j为头结点右子树节点数量]
dp[i] += dp[j] * dp[i - j-1]; ,dp[j]为j为头结点左子树节点数量,dp[i - j-1]为以j为头结点右子树节点数量
3.递推初始化
题目说了,n>=1
dp[1] = 1
4.确定遍历顺序
dp[i] += dp[j] * dp[i - j-1];
可以看出,节点数为i的状态是依靠 i之前节点数的状态。
那么遍历i里面每一个数作为头结点的状态,用j来遍历
for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[j - 1] * dp[i - j];}
}5.举例推导dp数组

如果自己画图举例的话,基本举例到n为3就可以了,n为4的时候,画图已经比较麻烦了。
正确代码:
class Solution {public int numTrees(int n) {int[] dp = new int[n+1];dp[1] = 1;dp[0] = 1;for(int i=2 ;i<=n ;i++){for(int j=0 ;j<=i-1;j++){dp[i] += dp[j]*dp[i-j-1];}}return dp[n];}
}注意:
虽然n=0时没有意义,但是实际写代码时发现,如果不对初始化dp[0] =1,循环里面也必须经过dp[0]这个循环。
因为我们在推导dp递推公式时,就用到了dp[0]
时间空间复杂度:
- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
这篇关于9.7不同的二叉搜索树(LC96-M)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




