【图形图像的C++ 实现 01/20】 2D 和 3D 贝塞尔曲线

2024-02-09 11:04
文章标签 c++ 实现 3d 01 20 贝塞尔 曲线 2d 图形图像

本文主要是介绍【图形图像的C++ 实现 01/20】 2D 和 3D 贝塞尔曲线，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

  • 一、说明
  • 二、贝塞尔曲线特征
  • 三、模拟
  • 四、全部代码如下
  • ​五、资源和下载

一、说明

   以下文章介绍了用 C++ 计算和绘制的贝塞尔曲线（2D 和 3D）。
   贝塞尔曲线具有出色的数学能力来计算路径（从起点到目的地点的曲线）。曲线的形状由“控制点”决定。所讨论的曲线最重要的特征是平滑度。
   在许多应用和领域中，平滑度是不可或缺的。我们可以考虑机器人或其他机器的运动，其中运动必须是可预测的，以确保人员和硬件的安全（低磨损系数）。当机器人关节的轨迹被计算为平滑路径时，我们可以假设机器人将按照规划的路径平滑地移动，不会出现急动或意外移动。请注意，在我们考虑的机器人技术中，除了路径之外，还有速度、加速度、冲击力和电机扭矩。所有这些参数主要影响最终路径。
   除了机器人技术之外，贝塞尔曲线还用于动画、游戏和设计。

   为了绘图的目的，我将使用我之前的文章中讨论过的 C++ 的 matplotlib 库。
   头文件（用于绘图库）必须与您的 cpp 位于同一文件夹中。您的程序可以按如下方式编译，

​//compile
g++ my_prog.cpp -o my_prog -I/usr/include/python3.8 -lpython3.8// 
//run
./my_prog
//folder tree
├── my_prog
├── my_prog.cpp
├── matplotlibcpp.h

​

二、贝塞尔曲线特征

   可以计算点集的贝塞尔曲线： { P0, P1, P2 …Pn}，其中n定义我们建模的曲线（多项式）的阶数。在每种情况下，第一个点和最后一个点定义曲线的起点和终点的位置。其他点 - 控制点通常不属于计算的曲线，而是影响贝塞尔曲线的形状。

   2D中的每个点P都有两个{x,y}笛卡尔坐标，但在3D中，点P按预期由三个{x, y, z}定义。

   贝塞尔曲线的显式定义可以指定如下（我们将在模拟中使用这个公式）。

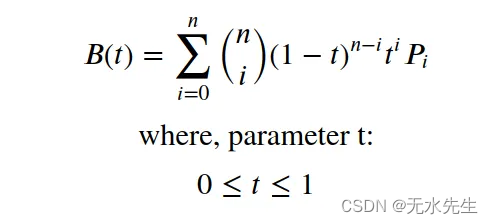
在这里插入图片描述
这里
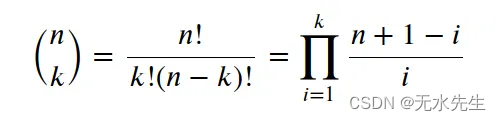
在这里插入图片描述

   是二项式系数。

   在我们的例子中，二项式系数的计算如下（如果您查看维基百科，您会发现递归实现，但这是最简单的版本或更直观）。

   C++ 中的实现可以如下所示，

​double computeBinominal(int n, int k)
{double value = 1.0;for (int i = 1; i <= k; i++){value = value * ((n + 1 - i) / i);}if (n == k){value = 1;}return value;
}

​
平面空间中的四个点P 0 、P 1 、P 2 和P 3 定义三次贝塞尔曲线。该曲线可以建模为三阶多项式。
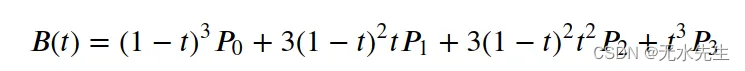
在这里插入图片描述

当提供六个点P 0、P 1、P 2、P 3、P4和P5时，贝塞尔曲线被计算为五阶多项式。

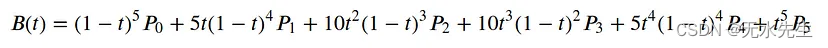
在这里插入图片描述

三、模拟

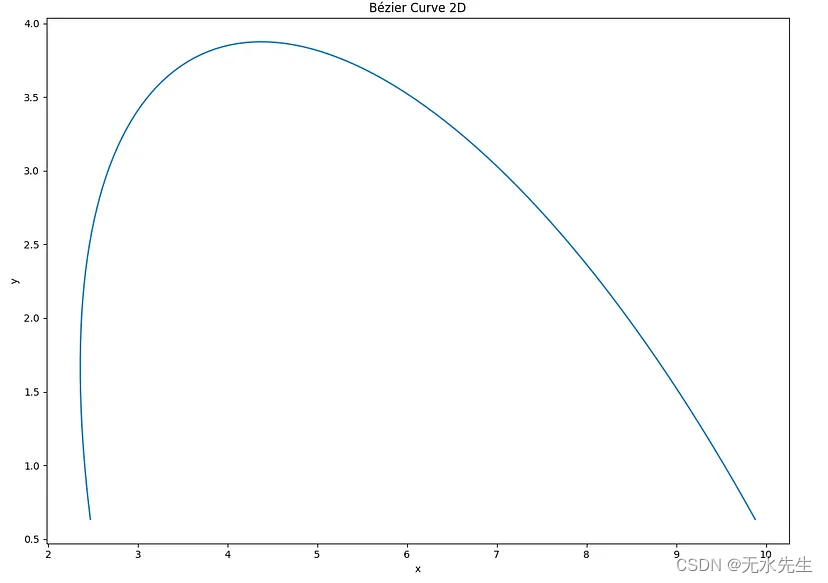
   现在我们将显示上面定义的曲线的 2D 和 3D 模拟（针对 4 点和 6 点）。下面的代码为您提供了计算和绘制您想要的任何数字点P 的贝塞尔曲线的绝佳机会。

x{2.5, 1.5, 6.0, 10.0}; 
y{0.5, 5.0, 5.0, 0.5};x{2.5, 1.5, 6.0, 10.0}; 
//与 2D y{0.5, 5.0, 5.0, 0.5}相同；
//与 2D z{1.0, 2.0, 3.0, 4.0}相同；X{2.5, 1.5, 6, 10, 7, 3}; 
Y{0.5, 5.0, 5.0, 0.5, 1.0, 2.0};X{2.5, 1.5, 6.0, 10.0, 7.0, 3.0}; // 对于 2D 
Y{0.5, 5.0, 5.0, 0.5, 1.0 , 2.0}; // 对于 2D 
Z{1.0, 2.0, 3.0, 4.0, 5.0, 0.1};

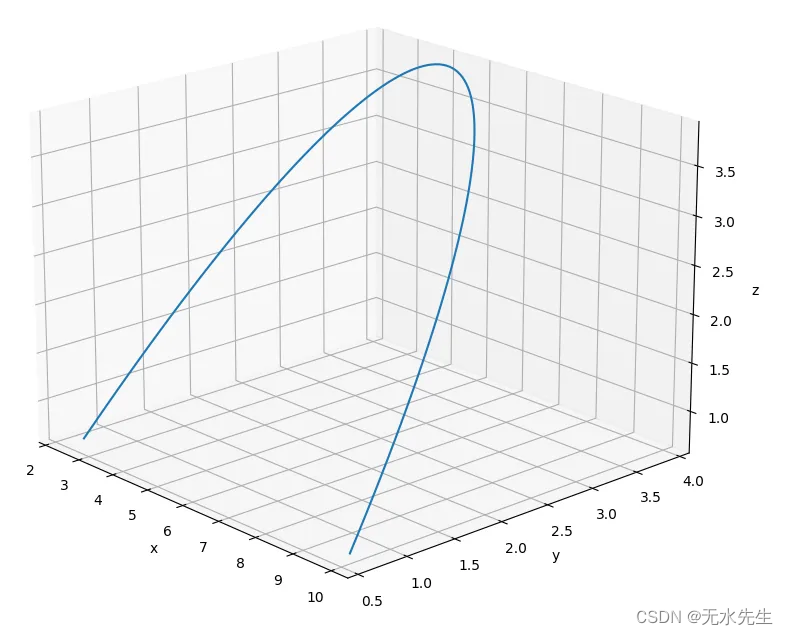
在这里插入图片描述
对于相同阶的多项式（三阶），我们可以计算 3D 贝塞尔曲线。

x{2.5, 1.5, 6.0, 10.0}; //same as 2D
y{0.5, 5.0, 5.0, 0.5}; //same as 2D
z{1.0, 2.0, 3.0, 4.0};

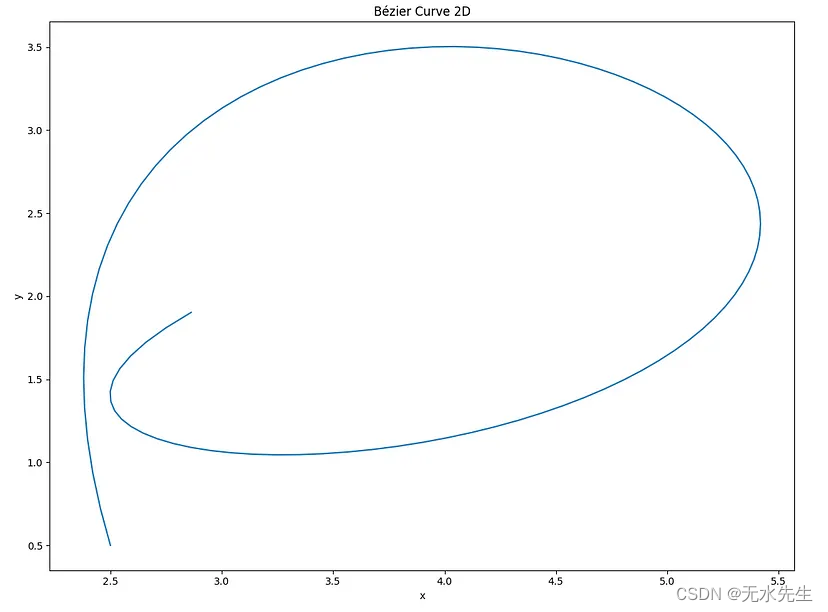
在这里插入图片描述
这是一条 2D 贝塞尔曲线，它是针对五阶多项式（六点）计算的。

X{2.5, 1.5, 6, 10, 7, 3};
Y{0.5, 5.0, 5.0, 0.5, 1.0 , 2.0};

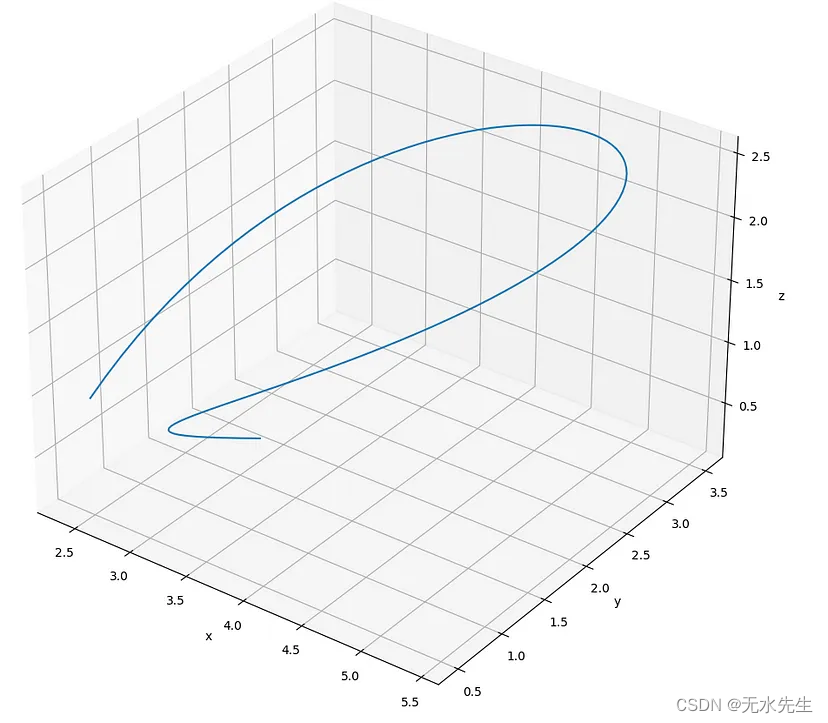
在这里插入图片描述
和以前一样，我们可以绘制 3D 贝塞尔曲线。

X{2.5, 1.5, 6.0, 10.0, 7.0, 3.0}; //as for 2D
Y{0.5, 5.0, 5.0, 0.5, 1.0 , 2.0}; //as for 2D
Z{1.0, 2.0, 3.0, 4.0, 5.0, 0.1};

在这里插入图片描述

四、全部代码如下

/// g++ bezier_curve.cpp -o t -I/usr/include/python3.8 -lpython3.8#include <iostream>
#include <vector>
#include <tuple>
#include <math.h>#include "matplotlibcpp.h"namespace plt = matplotlibcpp;//-----------------------------------------------------------std::tuple<std::vector<double>, std::vector<double>> computeBesierCurve2D(std::vector<double> xX, std::vector<double> yY)
{std::vector<double> bCurveX;std::vector<double> bCurveY;double bCurveXt;double bCurveYt;for (double t = 0.01; t <= 1; t += 0.01){bCurveXt = std::pow((1 - t), 3) * xX[0] + 3 * std::pow((1 - t), 2) * t * xX[1] + 3 * std::pow((1 - t), 1) * std::pow(t, 2) * xX[2] + std::pow(t, 3) * xX[3];bCurveYt = std::pow((1 - t), 3) * yY[0] + 3 * std::pow((1 - t), 2) * t * yY[1] + 3 * std::pow((1 - t), 1) * std::pow(t, 2) * yY[2] + std::pow(t, 3) * yY[3];bCurveX.push_back(bCurveXt);bCurveY.push_back(bCurveYt);}return std::make_tuple(bCurveX, bCurveY);
}//-----------------------------------------------------------void plot2D(std::tuple<std::vector<double>, std::vector<double>> data)
{std::vector<double> xX = std::get<0>(data);std::vector<double> yY = std::get<1>(data);plt::plot(xX, yY);plt::show();
}//-----------------------------------------------------------std::tuple<std::vector<double>, std::vector<double>, std::vector<double>> computeBesierCurve3D(std::vector<double> xX, std::vector<double> yY, std::vector<double> zZ)
{std::vector<double> bCurveX;std::vector<double> bCurveY;std::vector<double> bCurveZ;double bCurveXt;double bCurveYt;double bCurveZt;for (double t = 0.01; t <= 1; t += 0.01){bCurveXt = std::pow((1 - t), 3) * xX[0] + 3 * std::pow((1 - t), 2) * t * xX[1] + 3 * std::pow((1 - t), 1) * std::pow(t, 2) * xX[2] + std::pow(t, 3) * xX[3];bCurveYt = std::pow((1 - t), 3) * yY[0] + 3 * std::pow((1 - t), 2) * t * yY[1] + 3 * std::pow((1 - t), 1) * std::pow(t, 2) * yY[2] + std::pow(t, 3) * yY[3];bCurveZt = std::pow((1 - t), 3) * yY[0] + 3 * std::pow((1 - t), 2) * t * yY[1] + 3 * std::pow((1 - t), 1) * std::pow(t, 2) * yY[2] + std::pow(t, 3) * yY[3];bCurveX.push_back(bCurveXt);bCurveY.push_back(bCurveYt);bCurveZ.push_back(bCurveZt);}return std::make_tuple(bCurveX, bCurveY, bCurveZ);
}//-----------------------------------------------------------void plot3Dexample()
{std::vector<double> xX;std::vector<double> yY;std::vector<double> zZ;double theta;double r;double z_inc = 4.0 / 99.0;double theta_inc = (8.0 * M_PI) / 99.0;for (double i = 0; i < 100; i += 1){theta = -4.0 * M_PI + theta_inc * i;zZ.push_back(-2.0 + z_inc * i);r = zZ[i] * zZ[i] + 1;xX.push_back(r * std::sin(theta));yY.push_back(r * std::cos(theta));}plt::plot3(xX, yY, zZ);plt::show();
}//-----------------------------------------------------------void plot3D(std::tuple<std::vector<double>, std::vector<double>, std::vector<double>> data)
{std::vector<double> xX = std::get<0>(data);std::vector<double> yY = std::get<1>(data);std::vector<double> zZ = std::get<2>(data);plt::plot3(xX, yY, zZ);plt::xlabel("x");plt::ylabel("y");plt::set_zlabel("z");plt::show();
}//-----------------------------------------------------------double computeBinominal(int n, int k)
{double value = 1.0;for (int i = 1; i <= k; i++){value = value * ((n + 1 - i) / i);}if (n == k){value = 1;}return value;
}//-----------------------------------------------------------std::tuple<std::vector<double>, std::vector<double>> computeNVertexBasierCurve2D(std::vector<double> xX, std::vector<double> yY)
{std::vector<double> bCurveX;std::vector<double> bCurveY;int n = xX.size() - 1;std::cout << "n :" << n << "\n";for (double t = 0.0; t <= 1.0; t += 0.01){double bCurveXt{0};double bCurveYt{0};for (int i = 0; i <= n; ++i){bCurveXt += computeBinominal(n, i) * std::pow((1 - t), (n - i)) * std::pow(t, i) * xX[i];bCurveYt += computeBinominal(n, i) * std::pow((1 - t), (n - i)) * std::pow(t, i) * yY[i];//std::cout << " t= "<< t<< " i=" << i << " bCurveXt=" << bCurveXt << " = " << computeBinominal(n, i)  << " * " << std::pow((1 - t), (n - i))  << " * " << std::pow(t, i) << " * " << xX[i] << std::endl;}bCurveX.push_back(bCurveXt);bCurveY.push_back(bCurveYt);}return std::make_tuple(bCurveX, bCurveY);
}std::tuple<std::vector<double>, std::vector<double>, std::vector<double>> computeNVertexBasierCurve3D(std::vector<double> xX, std::vector<double> yY, std::vector<double> zZ)
{std::vector<double> bCurveX;std::vector<double> bCurveY;std::vector<double> bCurveZ;int n = xX.size() - 1;std::cout << "n :" << n << "\n";for (double t = 0.0; t <= 1.0; t += 0.01){double bCurveXt{0};double bCurveYt{0};double bCurveZt{0};for (int i = 0; i <= n; ++i){bCurveXt += computeBinominal(n, i) * std::pow((1 - t), (n - i)) * std::pow(t, i) * xX[i];bCurveYt += computeBinominal(n, i) * std::pow((1 - t), (n - i)) * std::pow(t, i) * yY[i];bCurveZt += computeBinominal(n, i) * std::pow((1 - t), (n - i)) * std::pow(t, i) * zZ[i];//std::cout << " t= "<< t<< " i=" << i << " bCurveXt=" << bCurveXt << " = " << computeBinominal(n, i)  << " * " << std::pow((1 - t), (n - i))  << " * " << std::pow(t, i) << " * " << xX[i] << std::endl;}bCurveX.push_back(bCurveXt);bCurveY.push_back(bCurveYt);bCurveZ.push_back(bCurveZt);}return std::make_tuple(bCurveX, bCurveY, bCurveZ);
}//-----------------------------------------------------------int main()
{std::vector<double> xX{2.5, 1.5, 6, 10};std::vector<double> yY{0.5, 5, 5, 0.5};std::vector<double> zZ{1.0, 2.0, 3.0, 4.0};std::tuple<std::vector<double>, std::vector<double>> bCurve2D = computeBesierCurve2D(xX, yY);plot2D(bCurve2D);std::tuple<std::vector<double>, std::vector<double>, std::vector<double>> bCurve3D = computeBesierCurve3D(xX, yY, zZ);plot3D(bCurve3D);std::vector<double> xXn{2.5, 1.5, 6, 10, 7, 3};std::vector<double> yYn{0.5, 5, 5, 0.5, 1.0 , 2.0};std::vector<double> zZn{1, 2, 3, 4, 5, 0.1};std::tuple<std::vector<double>, std::vector<double>> bCurve2DxN = computeNVertexBasierCurve2D(xXn, yYn);plot2D(bCurve2DxN);std::tuple<std::vector<double>, std::vector<double>, std::vector<double>> bCurve3DxN = computeNVertexBasierCurve3D(xXn, yYn, zZn);plot3D(bCurve3DxN);}

​五、资源和下载

下面给出源代码资源下载链接地址：
https://download.csdn.net/download/gongdiwudu/88821722

​

​

​​

​

这篇关于【图形图像的C++ 实现 01/20】 2D 和 3D 贝塞尔曲线的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/694041。

相关文章

Python使用Matplotlib绘制3D曲面图详解

Python使用Matplotlib绘制3D曲面图详解

《Python使用Matplotlib绘制3D曲面图详解》：本文主要介绍Python使用Matplotlib绘制3D曲面图,在Python中,使用Matplotlib库绘制3D曲面图可以通过mpl... 目录准备工作绘制简单的 3D 曲面图绘制 3D 曲面图添加线框和透明度控制图形视角Matplotlib
阅读更多...
使用Python实现IP地址和端口状态检测与监控

使用Python实现IP地址和端口状态检测与监控

《使用Python实现IP地址和端口状态检测与监控》在网络运维和服务器管理中,IP地址和端口的可用性监控是保障业务连续性的基础需求,本文将带你用Python从零打造一个高可用IP监控系统,感兴趣的小伙... 目录概述：为什么需要IP监控系统使用步骤说明1. 环境准备2. 系统部署3. 核心功能配置系统效果展
阅读更多...
Python实现微信自动锁定工具

Python实现微信自动锁定工具

《Python实现微信自动锁定工具》在数字化办公时代,微信已成为职场沟通的重要工具,但临时离开时忘记锁屏可能导致敏感信息泄露,下面我们就来看看如何使用Python打造一个微信自动锁定工具吧... 目录引言：当微信隐私遇到自动化守护效果展示核心功能全景图技术亮点深度解析1. 无操作检测引擎2. 微信路径智能获
阅读更多...
C#如何调用C++库

C#如何调用C++库

《C#如何调用C++库》：本文主要介绍C#如何调用C++库方式,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录方法一：使用P/Invoke1. 导出C++函数2. 定义P/Invoke签名3. 调用C++函数方法二：使用C++/CLI作为桥接1. 创建C++/CL
阅读更多...
Python中pywin32 常用窗口操作的实现

Python中pywin32 常用窗口操作的实现

《Python中pywin32常用窗口操作的实现》本文主要介绍了Python中pywin32常用窗口操作的实现,pywin32主要的作用是供Python开发者快速调用WindowsAPI的一个... 目录获取窗口句柄获取最前端窗口句柄获取指定坐标处的窗口根据窗口的完整标题匹配获取句柄根据窗口的类别匹配获取句
阅读更多...
在 Spring Boot 中实现异常处理最佳实践

在 Spring Boot 中实现异常处理最佳实践

《在SpringBoot中实现异常处理最佳实践》本文介绍如何在SpringBoot中实现异常处理,涵盖核心概念、实现方法、与先前查询的集成、性能分析、常见问题和最佳实践,感兴趣的朋友一起看看吧... 目录一、Spring Boot 异常处理的背景与核心概念1.1 为什么需要异常处理？1.2 Spring B
阅读更多...
Python位移操作和位运算的实现示例

Python位移操作和位运算的实现示例

《Python位移操作和位运算的实现示例》本文主要介绍了Python位移操作和位运算的实现示例,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一... 目录1. 位移操作1.1 左移操作 (<<)1.2 右移操作 (>>)注意事项：2. 位运算2.1
阅读更多...
如何在 Spring Boot 中实现 FreeMarker 模板

如何在 Spring Boot 中实现 FreeMarker 模板

《如何在SpringBoot中实现FreeMarker模板》FreeMarker是一种功能强大、轻量级的模板引擎,用于在Java应用中生成动态文本输出（如HTML、XML、邮件内容等）,本文... 目录什么是 FreeMarker 模板？在 Spring Boot 中实现 FreeMarker 模板1. 环
阅读更多...
Qt实现网络数据解析的方法总结

Qt实现网络数据解析的方法总结

《Qt实现网络数据解析的方法总结》在Qt中解析网络数据通常涉及接收原始字节流,并将其转换为有意义的应用层数据,这篇文章为大家介绍了详细步骤和示例,感兴趣的小伙伴可以了解下... 目录1. 网络数据接收2. 缓冲区管理（处理粘包/拆包）3. 常见数据格式解析3.1 jsON解析3.2 XML解析3.3 自定义
阅读更多...
SpringMVC 通过ajax 前后端数据交互的实现方法

SpringMVC 通过ajax 前后端数据交互的实现方法

《SpringMVC通过ajax前后端数据交互的实现方法》：本文主要介绍SpringMVC通过ajax前后端数据交互的实现方法,本文给大家介绍的非常详细,对大家的学习或工作具有一定的参考借鉴价... 在前端的开发过程中，经常在html页面通过AJAX进行前后端数据的交互，SpringMVC的controll
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2