学习笔记|多样本单因素方差分析|事后比较|方差齐性|F检验|韦尔奇检验|两独立样本T检验|两样本方差分析|规范表达|《小白爱上SPSS》课程：SPSS第七讲 | 单因素方差分析怎么做？

学习目的

SPSS第七讲 | 单因素方差分析怎么做？

软件版本

IBM SPSS Statistics 26。

原始文档

《小白爱上SPSS》课程
#统计原理

单因素方差分析

前面我们学习过，两独立样本T检验主要用于两组连续型正态分布的数据比较。但如果需要比较多组（三组及以上）的连续型数据，T检验分析方法就不合适了。此时，必须要借助单因素方差分析（One Way ANOVA）。
方差分析用于检验三个或三个以上的样本均数是否存在差异，是统计大神Fisher发明的，为了纪念他，方差分析又称为“F检验”。
其假设检验如下：
H0: 各组均数相等，μ1=μ2……=μk；
H1：各组均数不全相等，μ1、μ2……μk不全相等
α=0.05。
统计F值=组间变异/组内变异。
根据统计量F值大小和对应p值作为判断的标准，若p≤0.05，拒绝H0，接受H1，即各样本的总体均数不全相等；反之，则接受H0，拒绝H1，各样本的总体均数全相等。

一、实战案例

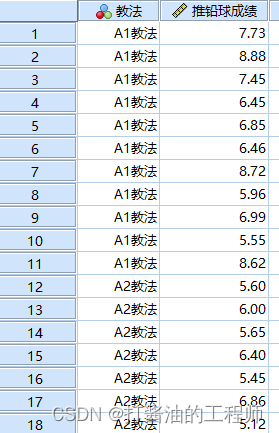
为了探讨不同教学方法对铅球教学效果的影响，小白将条件基本相近的33名学员分为了3组，分别实施以A1、A2和A3三种不同教学方法，经过一学期的教学，测得成绩如下，试问不同的教学方法之间是否存在着差异?
读取数据：

GET FILE='E:\*************\小白爱上SPSS\小白数据\第七讲 单因素方差分析.sav'. 

二、统计策略

统计分析策略口诀“目的引导设计，变量确定方法”
针对上述案例，扪心七问。
Q1：本案例研究目的是什么？
A：比较差异。
Q2：比较的组数是多少呢？
A：比较三组，这三组相互独立。
Q3：本案例属于什么研究设计？
A：实验性研究。
Q4：有几个变量？
A：有两个变量。教法和铅球成绩两个变量。
Q5：变量类型是什么？
A：教法为分组（分类）变量，分成A1、A2和A3三种教法;
铅球成绩为连续型变量。
Q6：连续型变量服从正态分布么？
A：需要检验。若服从，采用方差分析；若不服从正态，采用多样本秩和检验。
Q7：两样本总体成绩的方差是否齐性？
A：需要检验（原假设：方差齐性检验符合）。如果不齐，看韦尔奇矫正结果。

三、SPSS操作

1、正态性检验

本案例需要对三组都进行正态性检验。原假设：数据符合正态分布。
命令行：

EXAMINE VARIABLES=推铅球成绩 BY 教法/PLOT HISTOGRAM NPPLOT /*若无此行，则不输出正态性检验表*//COMPARE GROUPS /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.

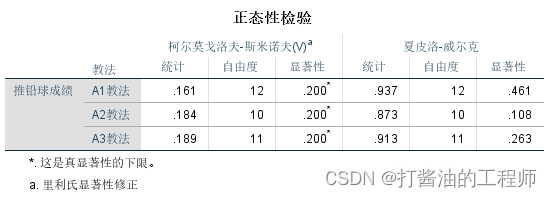
经S-W（夏皮洛-威尔克）检验，三组的铅球成绩的p值分别为0.461、0.108和0.263，均大于0.05，无统计学意义(接受原假设)，可认为三组数据符合正态分布。

2、单因素方差分析

Step1：依次点击“分析——比较平均值——单因素ANOVA”。
Step2: “单因素方差分析”窗口中，将因变量“推铅球成绩”放入“因变量列表”选项框中，将处理因素“教法”放入“因子”选项框中。
Step3: “单因素方差分析”窗口中点击“事后比较”选项，出现“单因素ANOVA：事后多重比较”窗口，在“假定方差齐性”栏下勾选“邦弗伦尼”方法，在“未假定方差齐性”栏下勾选“塔姆黑尼”方法，然后点击“继续”。

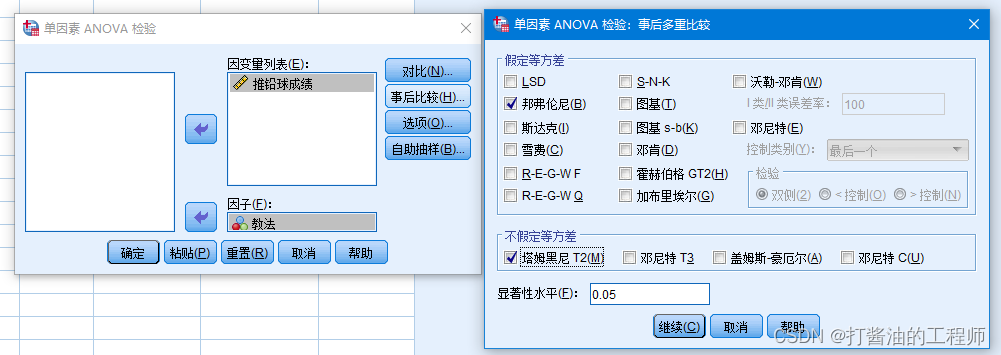
Tips:事后比较

事后比较：英文为Post Hoc Comparison。所谓事后比较，俗称马后炮分析，指的是一个研究项目设计时未事先制定比较的组别和方法，而在统计分析阶段进行任意组别的均数两两比较。虽然在方差分析过程中，我们会选择一些检验方法。但在输出结果中，只有整体的F值，达到显著性水平，即p<0.05时，才会报告事后多重比较结果。
SPSS的事后比较方法分成假定等方差（方差齐性）和不假定等方差（方差不齐）两种方式，共18种检验，够狠的，让科研小白如何选择？在此，简单介绍下。
（1）方差齐性
LSD最灵敏的方法，相当于t检验，并没有控制假阳性错误。因此想要得到更多阳性结果，则采用此法；
Bonferroni（邦弗伦尼）是保守的方法，它的思想是调整检验水准，根据比较的次数重新设定检验水准，然后根据P值做出结论，是临床研究最流行的一种方法；
SNK法是先按多组均值大小排序，然后按一个有点类似于t检验的公式分别比较（不过误差计算不同）
Turkey（图基） 和Scheffe（雪费）法是比较折中方法。
如果比较的各组样本量相等，Tukey法效率较高，所以样本量相似的时候，可以采用Tukey方法；如果样本量不同，则推荐Scheffe。
（2）方差不齐
一般选择塔姆黑尼法即可。
Step4: “单因素方差分析”窗口中点击“选项”，出现“单因素ANOVA：选项”窗口，勾选“描述性”和“方差同质性检验”和“韦尔奇”，然后点击“继续”。

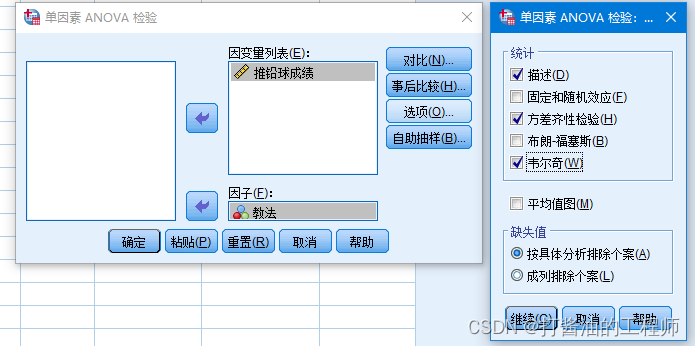
①描述：描述不同组的结局的均数、标准差、95%CI置信区间。
②方差齐性检验：对方差分析的条件之一“方差齐性”检验。
③韦尔奇：这是一种F检验替代，当方差不齐时进行使用。
Step5：点击“确定”后，就可呈现方差分析结果。
命令行：

ONEWAY 推铅球成绩 BY 教法 /STATISTICS DESCRIPTIVES HOMOGENEITY WELCH /MISSING ANALYSIS /POSTHOC=BONFERRONI T2 ALPHA(0.05).

四、结果解读

根据上述SPSS操作，F检验统计分析以下结果:

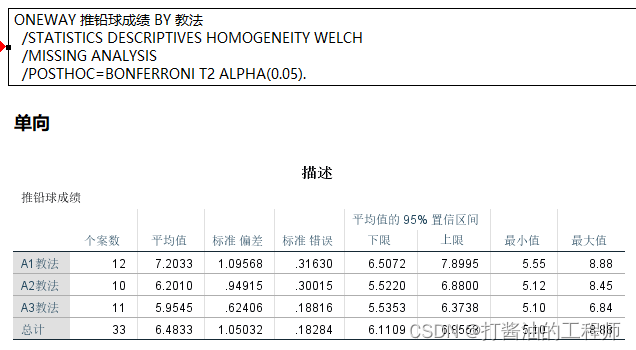
第一、统计描述

包括均数、标准差、95%CI置信区间、最小值和最大值等。

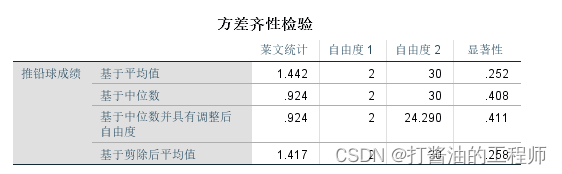
第二、方差齐性检验。

可选择第一行基于平均数结果。结果显示方差齐性检验p=0.252，大于0.05(无统计学意义，接受原假设：方差齐性检验符合)，方差齐性，可采用F检验。

第三、F检验结果

结果显示F=6.006，p=0.006<0.05(具有统计学意义，不接受原假设：不存在显著性差异)，说明多组总体均数存在显著性差异。

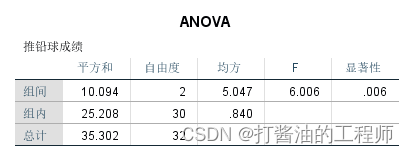
①F值，为本表中组间均方除以组内均方，F=5.047÷0.840=6.006。
②显著性，即p值。p=0.006<0.05(具有统计学意义，不接受原假设：不存在显著性差异)。

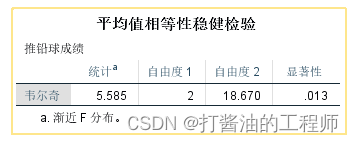
第四、韦尔奇检验

这是F检验的在方差不齐时的替代方法。本案例方差齐性，故不采用Welch 检验。当然， Welch检验结果显示，p=0.013，也表明多组存在着统计学差异。

第五、多重均数比较结果。

如果方差齐性，则看Bonferroni（邦弗伦尼）结果。如果方差不齐，则看塔姆黑尼的检验结果。

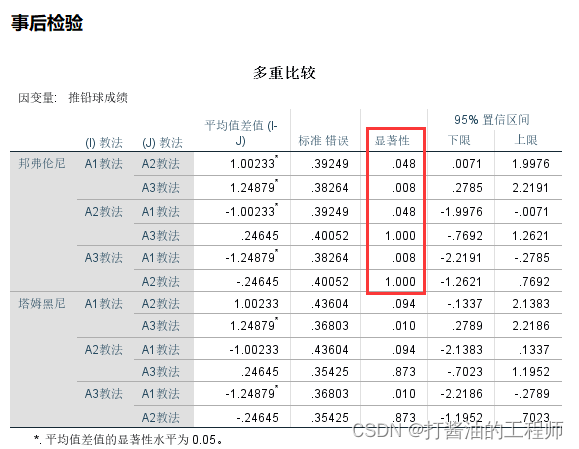
本案例方差齐性，故查看Bonferroni（邦弗伦尼）检验结果。原假设：成绩之间无显著性差异。各组两两之间是否有差异，主要依据显著性p值，如果P≤0.05，具有统计学意义，不接受原假设，表明存在显著性差异。
结果显示，A1与A2教法的铅球成绩存有显著性差异（p=0.048，具有统计学意义，不接受原假设）, A1与A3教法的铅球成绩存有显著性差异（p=0.008），而A2和A3教法的铅球成绩之间无显著性差异（p=1.000，无统计学意义，接受原假设）。

五、规范报告

规范报告有多种方式，本公众号只提供一种方式供参考。

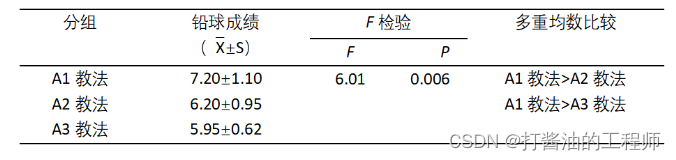
1、规范表格

表 不同教法对铅球成绩的影响

2、规范文字

方差分析结果显示，不同教法对铅球成绩有显著的不同影响，F=6.01,p=0.006。
Bonferroni多重均数比较结果显示，A1教法显著优于A2教法和A3教法，而A2和A3教法之间无显著性差异。

六、拓展阅读

1、多组均数比较为何不能用两两T检验比较？
小白学到似乎明白了，多组均数F检验只能说明多组之间总体均数不全相同，但不能说明任何两组之间存在着统计学差异。当存在显著性结果时，则采用多重比较的方法（俗称两两比较），以探索两组之间有没有统计学差异。
那为啥不能用之前学过的两独立样本T检验，进行两两多次比较呢？
答案是不能。多组数据两两比较用t检验会增加一类错误α，也就是假阳性错误。这意味着本来研究应该是阴性结果，但如果两两比较用t检验，其结果可能就是阳性。
一般情况下，一项研究的一类错误α值设定为0.05，因此， 当p≤0.05,有统计学意义的结论。但是这个结论存在一定的风险，或者说，该结论可能5%的可能性是错误的，是假的阳性结论。
5%的假阳性是公认的可以被接受的，但是如果一个项目多次两两比较，假阳性的概率可不是5%的概率了。
原理如下：当有k个均数需作两两比较时，同时比较的次数共有c= k(k-1)/2。设每次检验所用Ⅰ类错误的概率水准为α，累积Ⅰ类错误的概率为α’，则在对同一实验资料进行c次t检验时，在样本彼此独立的条件下，根据概率乘法原理，其累积Ⅰ类错误概率α’与c有下列关系：α’＝1－(1－α)c 。例如，本案例中设α＝0.05，c就是组数，为3组，其累积Ⅰ类错误的概率为α’＝1－(1-0.05)3=1-(0.95)3 = 0.143
本来假设检验假阳性错误是5%，现在有14.3%，，就容易把没有显著性结果说成了有显著性结果，把阴性结果说成阳性，这显然不合适的。
2、两组比较能用方差分析吗？
答案：能
两样本均数比较，也可以用F检验，而且两样本t检验和两样本F检验的结果是一致的。
比如，以第五讲的《两独立样本T检验》为例。
命令行：

GET FILE='E:\**********\小白爱上SPSS\小白数据\第五讲：两独立样本t 检验.sav'. 

两独立样本T检验

结果如下:
命令行：

T-TEST GROUPS=zb(1 2) /MISSING=ANALYSIS /VARIABLES=x /CRITERIA=CI(.95).

两样本方差分析

结果如下:
命令行：

ONEWAY x BY zb /STATISTICS DESCRIPTIVES HOMOGENEITY WELCH /MISSING ANALYSIS /POSTHOC=BONFERRONI T2 ALPHA(0.05).

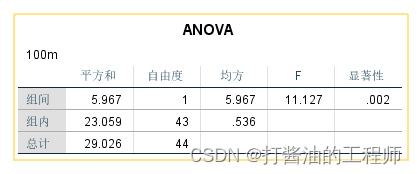
可以看出，两个结果p=0.002，没有任何差别。而且我们还发现，两样本的F值是T值的平方。F值:11.127=T值:-3.336*T值:-3.336。因此，F值与T之间存有内在的逻辑性。
小白学到这里，渐入佳境，越来越爱上统计学了，而且善于思考了。
他想：三个独立样本不能用T检验，那么三个匹配样本，比如同一受试者在实验过程中重复测试三次，应该也不能用配对样本T检验。
是的，小白统计思维是正确的，下一讲将讲解：单因素重复测量方差分析。

划重点

1、单因素方差分析用于检验多个（一般三组及以上）独立样本均数是否存在差异。
2、单因素方差分析的统计策略是：分组变量分成独立三组或三组以上，结局变量要求满足连续性、正态性和方差齐性。
3、当方差分析结果达到显著性水平（p≦0.05），只能说明多组之间总体均数不全相同。若要明确哪两组均数之间有差异，则需要事后多重比较；如果方差结果不显著，则不需要事后多重检验。
4、当连续型变量不满足正态性，则采用多样本秩和检验；如果方差不齐，建议查看韦尔奇检验矫正结果。
5、两组均数比较可采用两独立样本T检验，也可采用单因素方差分析；三组及三组以上，则只能采用单因素方差分析。