Nicn的刷题日常之杨氏矩阵（三种方法求解，逐级递增详解，手把手教学，建议三连收藏）

本文主要是介绍Nicn的刷题日常之杨氏矩阵（三种方法求解，逐级递增详解，手把手教学，建议三连收藏），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.杨氏矩阵知识普及：什么是样式矩阵

2.题目描述

3.解题

3.1暴力求解，遍历法

3.2巧妙解题：对角元素法

3.3将巧解法封装为函数

4.结语

1.杨氏矩阵知识普及：什么是样式矩阵

杨氏矩阵，是对组合表示理论和舒伯特演算很有用的工具。它提供了一种方便的方式来描述对称和一般线性群的群表示，并研究它们的性质。有一个二维数组. 数组的每行从左到右是递增的，每列从上到下是递增的. 在这样的数组中查找一个数字是否存在。时间复杂度小于O(N);

而在C语言中，我们通常理解的矩阵就是二维数组，那么

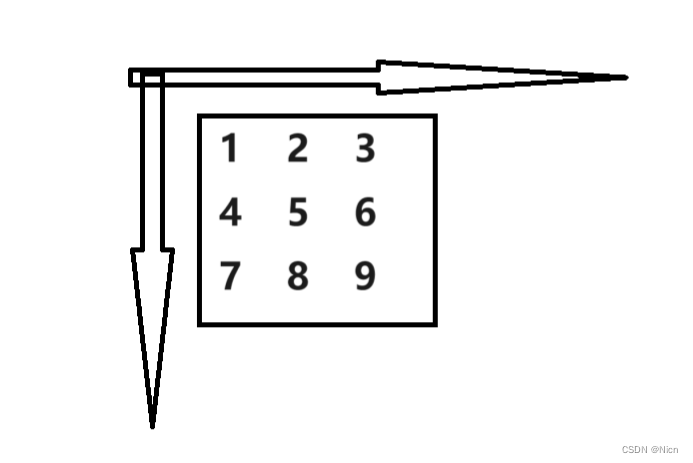
即是一个杨氏矩阵。

2.题目描述

有一个数字矩阵，矩阵的每行从左到右是递增的，矩阵从上到下是递增的，请编写程序在这样的矩阵中查找某个数字是否存在。

要求：时间复杂度小于O(N);

补充时间复杂度：假设数组有N个元素，遍历这个数组的每个元素去找数字最坏的情况就是将所有元素都遍历一遍，找N次，这时就称时间复杂度为O(n)

时间复杂度描述的是速率，描述最坏的数量积

3.解题

3.1暴力求解，遍历法

这个办法实现的思想是通过遍历数组的每一个元素来找到某个符合要求的数字，如果1考虑最坏的情况，满足要求的数字刚好是最后一个，那就得把数组从第一个元素到最后一个元素都遍历一遍。这样时间复杂度为O(n)，但不失为一种办法，我们来实现一下。

int main()
{int arr[3][3] = { 1,2,3,4,5,6,7,8,9 };int input = 0;printf("请输入您要查找的数字：>");scanf("%d", &input);int i = 0;int j = 0;for (i = 0; i < 3; i++){for (j = 0; j < 3; j++){if (arr[i][j] == input){printf("找到了，下标是%d %d\n", i, j);return;}}}printf("很遗憾没有这个数");return 0;
}

让我们来看一下运行效果：

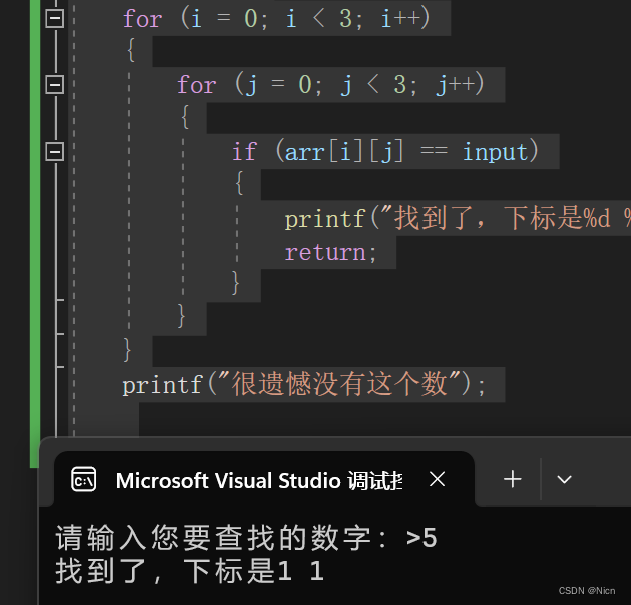
那我们刚才也说了，遍历法虽然是可行的但是却达不到我们的时间复杂度要求，所以我们得改进方法，介绍我们的第二种方法对角元素法：

3.2巧妙解题：对角元素法

对于杨氏矩阵来说，有四个位置的数字是特别的，就是四个对角上的元素：

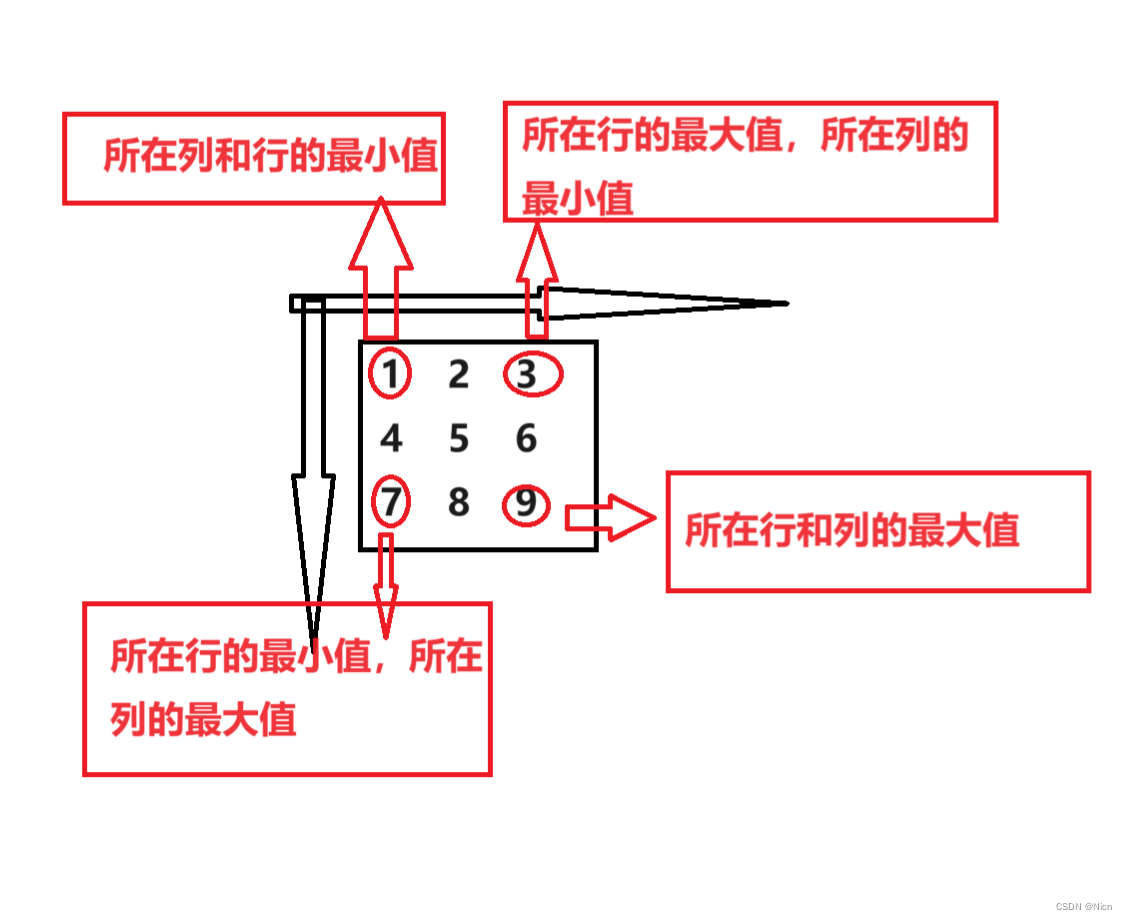
既然如此我们就可以利用数字3和7这两个位置中的任意一个，例如我们就利用3来查找5：

首先将3和5作比较，由于3是第一行最大元素都小于5，那么第一行的元素就排除，我们行数+1，我们看第二行对应1第一行3的位置的数是6，与5比较大于5，那说明要查找的数5就在第二行当时所在位数的列数小于6所在的列数，所以我们行数确定，列数-1，就找到了5.

我们来看一下实现过程：

int main()
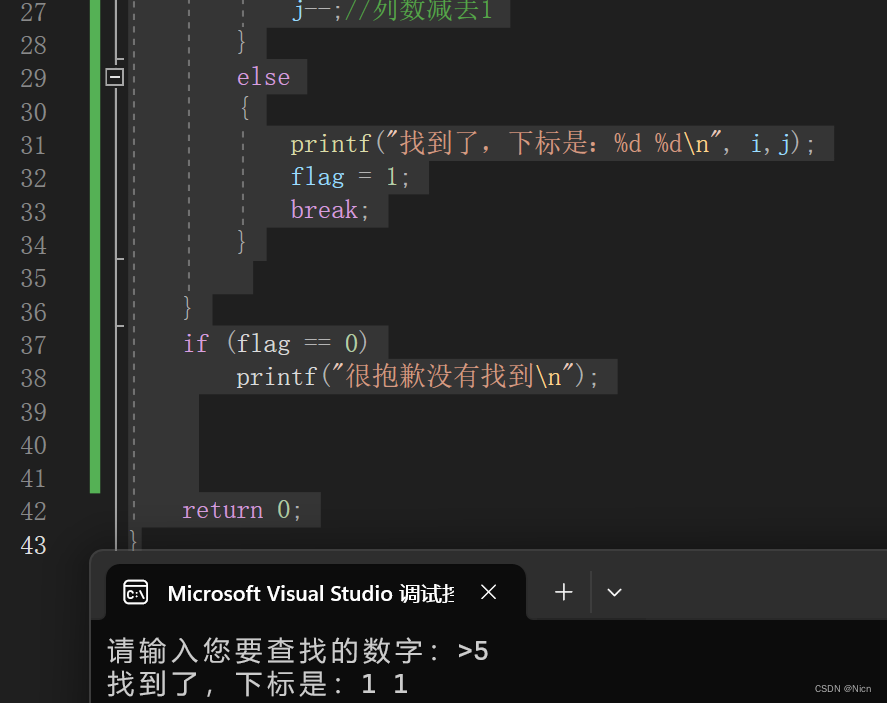
{int arr[3][3] = { 1,2,3,4,5,6,7,8,9 };int input = 0;printf("请输入您要查找的数字：>");scanf("%d", &input);int i = 0;int j = 2;int flag = 0;while (i<=2&&j>=0){if (arr[i][j] < input){i++;//行数增加，列数不变}else if (arr[i][j] > input){j--;//列数减去1}else{printf("找到了，下标是：%d %d\n", i,j);flag = 1;break;}}if (flag == 0)printf("很抱歉没有找到\n");return 0;
}

3.3将巧解法封装为函数

当封装为一个查找函数的时候，我们就不应该在函数内部进行打印，而是应该在函数外部进行打印，那我们的函数就应该要返回横纵坐标，

这样写可以吗？

return x,y;

明显这样的返回值是错误的，x,y会被当做为一个逗号表达式进行看待。

所以这里我是直接进行传地址，利用指针传参。我们看一下实现：

void Yang_table_serch(int arr[3][3], int k, int* r, int* c)
{int i = 0;int j = *c - 1;int flag = 0;while (i <= *c-1 && j >= 0){if (arr[i][j] < k){i++;//行数增加，列数不变}else if (arr[i][j] >k){j--;//列数减去1}else{*r = i;*c = j;flag = 1;return;}}if (flag == 0)*r = -1;*c = -1;return;}
int main()
{int arr[3][3] = { 1,2,3,4,5,6,7,8,9 };int input = 0;printf("请输入您要查找的数字：>");scanf("%d", &input);int i = 0;int j = 2;Yang_table_serch(arr, input, &i, &j);if (i == -1 && j == -1){printf("没有找到\n");}else{printf("找到了，下标是：%d %d\n", i, j);}return 0;
}