uniswap v3 中的tick管理

首先看一下tick的存储结构

struct Info {// 所有引用这个tick的position的流动性总和uint128 liquidityGross;//当tick被从左到右（从右到左）穿过时，流动性应该增加或减少的数值int128 liquidityNet;。。。}

其他字段和本节无关暂且略过。

比方说有两个 position 中的流动性相等，例如 L = 500，并且这两个 position 同时引用了一个 tick，其中一个为 lower tick ，另一个为 upper tick，那么对于这个 tick，它的 liquidityNet = +500-500=0。而liquidityGross=500+500=1000

当价格变动导致 tickcurrent 越过一个 position 的 lower/upper tick 时，我们需要根据 tick 中记录的值来更新当前价格所对应的总体流动性。假设 position 的流动性值为 ΔL，会有以下四种情况：

价格上涨，从左到右穿过一个 lower tick：liquidityNet = liquidityNet + ΔL；

价格上涨，从左到右穿过一个 upper tick：liquidityNet = liquidityNet - ΔL；

价格下降，从右到左穿过一个 upper tick：liquidityNet = liquidityNet + ΔL；

价格下降，从右到左穿过一个 lower tick：liquidityNet = liquidityNet - ΔL；

tick状态存储

uniswap v3 版本对价格的计算为了减少开根号的的计算成本直接存储的是,并且使用Q64.94精度的定点数来保存。首先解释下这个Q64.94代表什么意思。

Q (number format)是一种指定二进制定点数的格式的方法。例如Q8.8表示的数字格式意味着这种格式中的定点数字整数部分有8位，小数数部分有8位。对于Q64.94而言，其代表的数值范围是0 至 。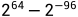

也就是说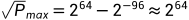而

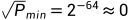
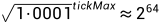对应的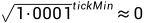

于是得出tickMax = 887272 为了做对应 tickMin = -887272

这就意味着v3版本的智能合约需要管理887272*2个tick，达到了百万级，这个数量是不小的。

而实际上这么多的tick其中绝大部分是没有必要初始化的。合约代码中对这些tick做了二级管理。

mapping(int16 => uint256) public override tickBitmap;

    function position(int24 tick) private pure returns (int16 wordPos, uint8 bitPos) {wordPos = int16(tick >> 8);bitPos = uint8(tick % 256);}

887272*2个tick合约中用int24来表示；int16(tick >> 8)代表取高16位，uint8(tick % 256)代表取低8位，在tickBitmap中高16位作为key，那么为什么用uint256作为value呢？剩下的低8位是2的8次方一共256个数。也就是说tickBitmap每一条记录需要管理256个tick状态，最高效的方法就是使用位图，把256个数转换成256个二进制数表示，也就是uint256，相应的位上为1代表当前的tick被引用。

tick转换为价格

我们知道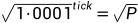,公式很简单，但是当我们要计算价格P的时候入股直接带入tick这个计算量是非常庞大的，比如tick=887272。uniswap在这能合约中的计算代码如下：

function getSqrtRatioAtTick(int24 tick) internal pure returns (uint160 sqrtPriceX96) {uint256 absTick = tick < 0 ? uint256(-int256(tick)) : uint256(int256(tick));require(absTick <= uint256(MAX_TICK), 'T');uint256 ratio = absTick & 0x1 != 0 ? 0xfffcb933bd6fad37aa2d162d1a594001 : 0x100000000000000000000000000000000;if (absTick & 0x2 != 0) ratio = (ratio * 0xfff97272373d413259a46990580e213a) >> 128;if (absTick & 0x4 != 0) ratio = (ratio * 0xfff2e50f5f656932ef12357cf3c7fdcc) >> 128;if (absTick & 0x8 != 0) ratio = (ratio * 0xffe5caca7e10e4e61c3624eaa0941cd0) >> 128;if (absTick & 0x10 != 0) ratio = (ratio * 0xffcb9843d60f6159c9db58835c926644) >> 128;if (absTick & 0x20 != 0) ratio = (ratio * 0xff973b41fa98c081472e6896dfb254c0) >> 128;if (absTick & 0x40 != 0) ratio = (ratio * 0xff2ea16466c96a3843ec78b326b52861) >> 128;if (absTick & 0x80 != 0) ratio = (ratio * 0xfe5dee046a99a2a811c461f1969c3053) >> 128;if (absTick & 0x100 != 0) ratio = (ratio * 0xfcbe86c7900a88aedcffc83b479aa3a4) >> 128;if (absTick & 0x200 != 0) ratio = (ratio * 0xf987a7253ac413176f2b074cf7815e54) >> 128;if (absTick & 0x400 != 0) ratio = (ratio * 0xf3392b0822b70005940c7a398e4b70f3) >> 128;if (absTick & 0x800 != 0) ratio = (ratio * 0xe7159475a2c29b7443b29c7fa6e889d9) >> 128;if (absTick & 0x1000 != 0) ratio = (ratio * 0xd097f3bdfd2022b8845ad8f792aa5825) >> 128;if (absTick & 0x2000 != 0) ratio = (ratio * 0xa9f746462d870fdf8a65dc1f90e061e5) >> 128;if (absTick & 0x4000 != 0) ratio = (ratio * 0x70d869a156d2a1b890bb3df62baf32f7) >> 128;if (absTick & 0x8000 != 0) ratio = (ratio * 0x31be135f97d08fd981231505542fcfa6) >> 128;if (absTick & 0x10000 != 0) ratio = (ratio * 0x9aa508b5b7a84e1c677de54f3e99bc9) >> 128;if (absTick & 0x20000 != 0) ratio = (ratio * 0x5d6af8dedb81196699c329225ee604) >> 128;if (absTick & 0x40000 != 0) ratio = (ratio * 0x2216e584f5fa1ea926041bedfe98) >> 128;if (absTick & 0x80000 != 0) ratio = (ratio * 0x48a170391f7dc42444e8fa2) >> 128;if (tick > 0) ratio = type(uint256).max / ratio;// this divides by 1<<32 rounding up to go from a Q128.128 to a Q128.96.// we then downcast because we know the result always fits within 160 bits due to our tick input constraint// we round up in the division so getTickAtSqrtRatio of the output price is always consistentsqrtPriceX96 = uint160((ratio >> 32) + (ratio % (1 << 32) == 0 ? 0 : 1));}

乍一看很懵，先了解一下背后的算法。

首先tick的取值范围是i属于[-887272,887272]，而任何正整数都可以表示为如下形式：

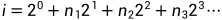
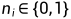
随便举个例子，比如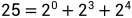

那么[1,887272]范围内的数表示如下

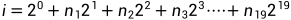
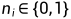
上面代码中的0x1，0x2，0x4...一直到0x80000就是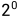一直到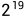的16进制表示

还是拿tick=25举例：

根据上面的公式推导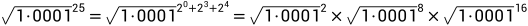

如果从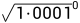到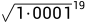我们都事先计算好的话，即便是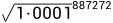也能将步骤简化成有限的几个数字相乘，很好的控制了计算量，这样的话下面这行代码就很好理解了。

if (absTick & 0x2 != 0) ratio = (ratio * 0xfff97272373d413259a46990580e213a) >> 128

ratio的初始值为1，如果tick的绝对值进行分解后，包含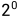，那么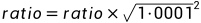

实际上在代码层面在上面的算法基础上还做了一层优化：

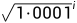当i为正数时，其计算结果有可能很大，中间涉及到的乘法运算可能会造成溢出，所以实际计算的是i为负数时的值，因为当i为负数时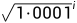，是一个小于1的小数，所以不会产生溢出，即上面代码中的那些魔数应当是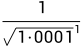,,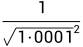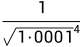.....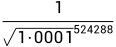。每一次计算要右移128位，只取高128位的数。

if (tick > 0) ratio = type(uint256).max / ratio;

最后这行代码的意思是，如果tick为正数，需要把计算的结果求导，即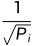,再用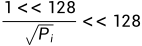转换为Q128.128格式，1<<256用type(uint256).max代替

sqrtPriceX96 =uint160((ratio >>32)+(ratio %(1<<32)==0?0:1));

分开两部分：

(ratio >>32)代表省略小数的后32位，

(ratio %(1<<32)==0?0:1)倒数第32位小数四舍五入。

总的来说就是把Q128.128 转换为 Q128.96.

未完待续。。。